Свободные гармоничесие колебания. Колебания с одной степенью свободы. Сложения колебаний. Биения. Фигуры Лиссажу

Билет 14.

Вопрос 2.

Среди различных процессов втречаются периодически повторяющиеся (колебания). Колебательный процесс может возникнуть за счёт внешней силы, которая вывела систему из равнвесия и перестала действовать, а колебания происходят под действием только внутренних сил, без участия внешних. Такие колебания наз. собственными. Колебания с одной степенью свободы – это колебания при которых движения системы можно описать одним независимым параметром (координатой). Пример: колебания математического маятника, колебания физического маятника (твёрдое тело, подвешенное за точку и способное колебаться вокруг оси, не проходящей через ц. м.), колебания груза на пружинке.

Уравнения для физического маятника: Je=–mgasina»–mgaa, приведённая длинна физического маятника, равна длинне математического маятника с тем же периодом – l=J₀+ma²/ma. T= 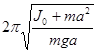, решение этого уравнения: a=a₀cos(wt+j), a₀, j определяются начальными условиями, w – параметр системы. 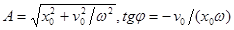Колебания происходящие по закону sinуса или cosинуса наз. гармоническими.

Сложение гармонических колебаний одинаковой частоты. x₁=A₁cos(wt+j₁), x₂=A₂cos(wt+j₂). Представим в комплексной форме: x=x₁+x₂=A₁e^i(wt+j1)+ A₂e^i(wt+j2)=e^iwt(A₁e^ij1+A₂e^ij2), A₁e^ij1+A₂e^ij2=Ae^ij, A²=A₁²+A₂²+2 A₁A₂cos(j₁–j₂,), tg j=(A₁sinj₁+A₂sinj₂)/(A₁cosj₁+A₂cosj₂) Þ x=x₁+x₂=Ae^i(wt+j) Þ x=Acos(w t–j).

Сложения гармонических колебаний с близкими частотами. x₁=A₁cos(w₁t+j₁), x₂=A₂cos(w₂t+j₂). Каждое из колебаний представим в комплексной форме, а сложение будем производить векторно. Пусть A₁>A₂. Cуммой двух колебаний с близкими частотами является колебание с изменяющейся амплитудой (от А₁–А₂ до А₁+А₂) и с частотой |w₁–w₂|. Колебания амплитуды с частотой W=|w₁–w₂| называются с биениями, а частота W – частотой биения.

Дата добавления: 2015-04-24