Примеры решения задач 2 страница. Решение. Доля энергии, переданной первым шаром второму, выразится соотношением:

Решение. Доля энергии, переданной первым шаром второму, выразится соотношением:

(1)

где — кинетическая энергия первого шара до удара; u ₂ и 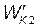, — скорость и кинетическая энергия второго шара после удара.

Как видно из выражения (1), для определения 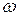надо найти u ₂. Воспользуемся тем, что при ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии.

По закону сохранения импульса, учитывая, что второй шар до удара покоился, имеем . По закону сохранения энергии в механике, 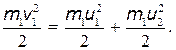Решая совместно два последних уравнения, найдем:

u ₂=2 m ₁ v ₁/(m ₁+ m ₂).

Подставив это выражение u ₂ в равенство (1), получим:

Из этого соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.

Пример 11. Боек (ударная часть) свайного молота массой т ₁=500 кг падает на сваю массой m ₂=100 кг со скоростью v ₁=4 м/с. Определить: 1) кинетическую энергию бойка в момент удара; 2) энергию , затраченную на углубление сваи в грунт; 3) кинетическую энергию 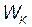, перешедшую во внутреннюю энергию системы; 4) КПД 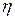удара бойка о сваю. Удар бойка о сваю рассматривать как неупругий.

Решение. 1. Кинетическую энергию бойка в момент удара о сваю находим по формуле = m ₁ v ₁²/2. Подставив значения m ₁, и v ₁ и произведя вычисления, получим:

=(500×4²)/2 Дж=4000 Дж=4 кДж.

2. Чтобы определить энергию, затраченную на углубление сваи, предварительно найдем скорость системы боек — свая непосредственно после удара. Для этого применим закон сохранения импульса, который в случае неупругого удара выражается формулой:

т ₁ v ₁+ m ₂ v ₂=(m ₁+ m ₂) u, (1)

где v ₂ — скорость сваи перед ударом; и — скорость бойка и сваи непосредственно после удара. Свая перед ударом находилась в состоянии покоя, поэтому v ₂=0. Так как удар неупругий, то боек и свая после удара движутся как одно целое, т. е. с одинаковой скоростью и. Из формулы (1) найдем эту скорость:

(2)

В результате сопротивления грунта скорость бойка и сваи после удара быстро гасится, а кинетическая энергия, которой обладает система боек — свая, затрачивается на углубление сваи в грунт.

Эту энергию находим по формуле Заменим скорость и ее выражением (2): 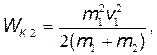или, учитывая, что = m ₁ v ₁²/2, запишем:

(3)

Подставив в формулу (3) значения т ₁, m ₂ и и произведя вычисления, получим:

= [500/(500+100)]. 4·10³ Дж=3,33·10³ Дж=3,33 кДж.

3. Боек до удара обладал энергией ; — энергия, затраченная на углубление сваи в грунт. Следовательно, во внутреннюю энергию, связанную с неупругой деформацией сваи, превратилась энергия:

= — .

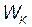Подставив в это выражение значения T ₁ и T ₂, найдем

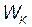=0,67 кДж.

4. Свайный молот служит для забивки сваи в грунт; следовательно, энергию следует считать полезной. КПД удара бойка о сваю выразится как отношение энергии , затраченной на углубление сваи в грунт, ко всей затраченной энергии :

= / .

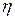Подставив в последнее выражение по формуле (3), получим

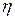=m₁/(m₁+m₂).

Подставим значения m ₁ и т ₂и произведем вычисления:

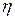=83,3%.

Пример 12. Вычислить момент инерции J_z молекулы NО₂ относительно оси z, проходящей через центр масс молекулы перпендикулярно плоскости, содержащей ядра атомов. Межъядерное расстояние d этой молекулы равно 0,118 нм, валентный угол =140°.

Решение. Молекулу NO₂ можно рассматривать как систему, состоящую из трех материальных точек общей массой

m =2 m ₁+ m ₂, (1)

где m ₁ — масса атома кислорода; m ₂ — масса атома азота.

Расположим молекулу относительно координатных осей так, как это указано на рис. 8 (начало координат совместим с центром масс С молекулы, ось z направим перпендикулярно плоскости чертежа «к нам».)

Для определения J_z воспользуемся теоремой Штейнера:

J=J _c+ ma ².

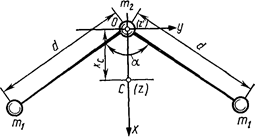Для данного случая эта теорема запишется в виде J_z' = J_z+ma ², где J_z' — момент инерции относительно оси z', параллельной оси z и проходящей через атом азота (точка О на рис. 8). Отсюда искомый момент инерции

J_z = J_z' –ma ² (2)

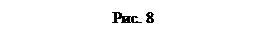Момент инерции J_z' находим как сумму моментов инерции двух материальных точек (атомов кислорода):

J_z' = 2m₁ d ² (3)

Расстояние а между осями z и z ' равно координате x_с центра масс системы и поэтому может быть выражено по формуле:

.

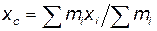В данном случае:

а = х _с= (2 m ₁ x ₁+ m ₂ x ₂)/(2 m ₁+ m ₂),

или, учитывая, что x ₁= d cos ( /2) и х ₂ = 0,

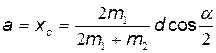(4)

Подставив в формулу (2) значения J_z', т, а соответственно из выражений (3), (1), (4), получим:

или после преобразований:

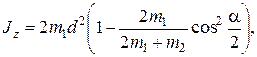(5)

Относительные атомные массы кислорода (A _O=16) и азота (А _N=14). Запишем массы атомов этих элементов в атомных единицах массы (а.е.м.), а затем выразим в килограммах (1 а.е.м. =1,66 ·10^-27 кг):

m ₁= 161,66·10^-27 кг=2,66·10^-26 кг;

m ₂ = 141,66·10^-27 кг = 2,32·10^-26 кг.

Значения m ₁, т ₂, d и подставим в формулу (5) и произведем вычисления:

J_z =6,80·10^-46 кг·м².

Пример 13. Физический маятник представляет собой стержень длиной l =1 м и массой m ₁=l кг с прикрепленным к одному из его концов диском массой т ₂ = 0,5 m ₁. Определить момент инерции J _zтакого маятника относительно оси Оz, проходящей через точку О на стержне перпендикулярно плоскости чертежа (рис. 9).

Решение. Общий момент инерции маятника равен сумме моментов инерции стержня J_z1 и диска J_z2.

J_z ⁼ J_z1 + J_z2 (1)

Формулы, по которым вычисляются моменты инерции стержня J_{z 1} и диска J_{z 2} относительно осей, проходящих через их центры масс, даны в табл. на с. 13. Чтобы определить моменты инерции J_{z 1} и J_{z 2}, надо воспользоваться теоремой Штейнера:

J=J_c+ma². (2)

Выразим момент инерции стержня согласно формуле (2):

J_z1=^l/₁₂m₁l²+m₁a₁².

Расстояние a ₁ между осью Оz и параллельной ей осью, проходящей через центр масс C ₁ стержня, как следует из рис. 9, равно ¹/₂ l ‑ ^l/₃ l= ^l/₆ l. С учетом этого запишем:

J_{z 1} = ^l/₁₂ m ₁ l ²+ m ₁ (^l/₆ l)²=¹/₉ m ₁ l ²=0,111 m ₁ l ².

Момент инерции диска в соответствии с формулой (2) равен:

J_{z 2}=^l/₂ m ₂ R ²+ m ₂ a ₂².

где R — радиус диска; R= ¹/₄ l. Расстояние а ₂ между осью Оz и параллельной ей осью, проходящей через центр масс диска, равно (рис. 9) ²/₃ l + ^l/₄ l= ^l1/₁₂ l. С учетом этого запишем:

J_{z 2}=^l/₂ m ₂ (¹/₄ l)²+ m ₂(^l1/₁₂ l)²= 0,0312 m ₂ l ² + 0,840 m ₂ l ²= 0,871 m ₂ l ².

Подставив полученные выражения J_z1 и J_z2 в формулу (1), найдем

J_z= 0,111 m ₁ l ²+0,871 m ₂ l ²=(0,111 m ₁+0,871 m ₂) l ²,

или, учитывая, что т ₂ = 0,5 m ₁,

J_z= 0,547 m ₁ l ².

Произведя вычисления, получим значение момента инерции физического маятника относительно оси Оz:

J_z =0,547·1·1 кг·м²=0,547 кг·м².

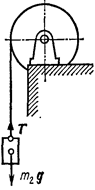
Пример 14. Вал в виде сплошного цилиндра массой m ₁ = 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m ₂=2 кг (рис. 10). С каким ускорением а будет опускаться гиря, если ее предоставить самой себе?

Решение. Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности,

и связано с угловым ускорением 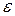вала соотношением:

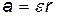, (1)

где r — радиус вала.

Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:

, (2)

где М — вращающий момент, действующий на вал; J — момент инерции вала. Рассматриваем вал как однородный цилиндр. Тогда его момент инерции относительно геометрической оси равен

J= ¹/₂ m ₁ r ².

Вращающий момент М, действующий на вал, равен произведению силы натяжения Т шнура на радиус вала: М=Тr.

Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести 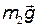, направленная вниз, и сила натяжения 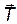шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m ₂ g – T=m₂a, откуда T=m₂ (g – а). Таким образом, вращающий момент M=m ₂(g—а) r.

Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала:

Для определения линейного ускорения гири подставим это выражение 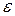в формулу (1). Получим

,

откуда

.

Пример 15. Через блок в виде диска, имеющий массу m =80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m ₁=100 г и m ₂=200 г (рис. 11). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движущихся грузов действуют две силы: сила тяжести , направленная вниз, и сила 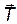натяжения нити, направленная вверх.

Так как вектор ускорения груза m ₁ направлен вверх, то T ₁> m ₁ g. Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна T ₁ – т ₁ g=т ₁ а, откуда:

T ₁ =m ₁ g+m ₁ a. (1)

Вектор ускорения груза т ₂ направлен вниз; следовательно, T ₂< m ₂ g. Запишем формулу второго закона для этого груза:

m ₂ g – T ₂ =m₂a, откуда

T ₂ =m₂g – m₂а. (2)

Согласно основному закону динамики вращательного движения, вращающий момент М, приложенный к диску,равен произведению момента инерции J диска на его угловое ускорение :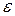

M=J 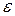. (3)

Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона, силы и , приложенные к ободу диска, равны соответственно силам T ₁ и Т ₂, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке; следовательно, > . Вращающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т. е. M =( – ) r. Момент инерции диска J=mr ²/2, угловое ускорение связано с линейным ускорением грузов соотношением 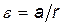. Подставив в формулу (3) выражения М, J и 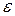, получим

( – ) r =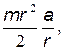

откуда

– =(т /2) а.

Так как =T ₁ и = Т ₂, то можно заменить силы и вы­ражениями по формулам (1) и (2), тогда:

m₂g – m₂a – m₁g – m₁a= (m/2) a, или(m₂—m₁) g= (m₂+m₁+m /2) a

откуда:

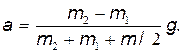(4)

Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому значения масс m ₁, m ₂ и m можно выразить в граммах, как они даны в условии задачи. После подстановки получим:

Пример 16. Маховик в виде диска массой m =50 кг и радиусом r =20 см был раскручен до частоты вращения 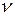₁=480 мин^-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t =50 с; 2) маховик до полной остановки сделал N= 200 оборотов.

Решение. 1.По второму закону динамики вращательного движения, изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:

M t=J — J ,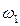

где J — момент инерции маховика; 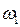и — начальная и конечная угловые скорости. Так как =0 и 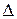t = t, то Mt= – J 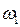, откуда:

M = – J 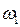/t. (1)

Момент инерции диска относительно его геометрической оси равен J=¹/₂mr². Подставив это выражение в формулу (1), найдем

M= – mr² 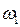/ (2 t). (2)

Выразив угловую скорость 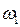через частоту вращения 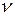₁ и произведя вычисления по формуле (2), найдем:

М= – 1 Н·м.

2. В условии задачи дано число оборотов, сделанных махови­ком до остановки, т. е. его угловое перемещение. Поэтому приме­ним формулу, выражающую связь работы с изменением кинетиче­ской энергии:

или, учтя, что ,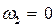

(3)

Работа при вращательном движении определяется по формуле A=Mj. Подставив выражения работы и момента инерции диска в формулу (3), получим:

M = – mr ² /4.

Отсюда момент силы трения:

М= – mr ² /4 . (4)

Угол поворота j= 2 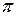N =2·3,14·200 рад=1256 рад. Произведя вычисления по формуле (4), получим:

М= – 1 Н·м.

Знак минус показывает, что момент силы трения оказывает тормозящее действие.

Пример 17. Платформа в виде диска радиусом R = 1,5 м и массой m ₁ = 180 кг вращается по инерции около вертикальной оси с часто­той 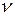=10 мин^-1. В центре платформы стоит человек массой т ₂=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. По закону сохранения момента импульса,

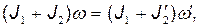(1)

где J ₁ — момент инерции платформы; J ₂ — момент инерции человека, стоящего в центре платформы; 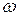— угловая скорость платформы с человеком, стоящим в ее центре; J₂' — момент инерции человека, стоящего на краю платформы; 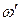— угловая скорость платформы с человеком, стоящим на ее краю.

Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением:

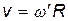. (2)

Определив 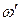из уравнения (1) и подставив полученное выражение в формулу (2), будем иметь:

v= (J ₁ +J ₂) 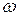R /(J ₁ +J' ₂). (3)

Момент инерции платформы рассчитываем как для диска; следовательно, J ₁= ¹1₂m ₁ R². Момент инерции человека рассчитываем как для материальной точки. Поэтому J ₂=0, J' ₂ =m ₂ R ². Угловая скорость платформы до перехода человека равна .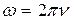

Заменив в формуле (3) величины J ₁, J ₂, J' ₂. и 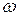их выражениями, получим:

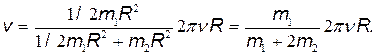
Сделав подстановку значений т ₁, т ₂, 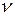, R и , найдем линейную скорость человека:

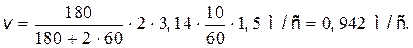
Пример 18. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения 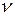₁=0,5 c^-1. Момент инерции j_o тела человека относительно оси вращения равен 1,6 кг·м². В вытянутых в стороны руках человек держит по гире массой m =2 кг каждая. Расстояние между гирями l ₁=l,6 м. Опре­делить частоту вращения 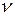₂, скамьи с человеком, когда он опустит руки и расстояние l ₂ между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.

Решение. Человек, держащий гири (рис. 12), составляет вместе со скамьей замкнутую механическую систему, поэтому момент импульса J 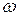этой системы должен иметь постоянное значение. Следовательно, для данного случая

J₁ 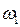= J₂ ,

где J и 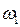— момент инерции тела человека и угловая скорость скамьи и человека с вытянутыми руками; J ₂ и — момент инерции тела человека и угловая скорость скамьи и человека с опу­щенными руками. Отсюда:

Дата добавления: 2015-03-29