
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уйгели В.В., Пратусевич А.Е., Корнаев А.В., Доронин О.Н. 3 страница
|
|
|
|
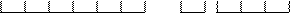 |
х е1 е
На самом деле, чтобы найти меру отрезка х при единице длины е1, достаточно найти число, показывающее сколько раз е1 укладывается в отрезке х.
 Искомое число будет равно в + в + в +…+ в = в · а = а · в. Значит, mе1 (х) = а · в.
Искомое число будет равно в + в + в +…+ в = в · а = а · в. Значит, mе1 (х) = а · в.
Таким образом, умножение натуральных чисел как мер длин отрезков выражает переход к новой (более мелкой) единице длины.
Пусть а = mе (х) и в = mе1 (е). Тогда произведением натуральных чисел а и в называется натуральное число а ∙ в, равное мере длины отрезка х при новой (более мелкой) единице длины е1.
В процессе обучения математике детям встречаются задачи с величинами, в которых рассматривается действие умножения. Определение смысла умножения натуральных чисел, являющихся значениями величин, позволяет обосновывать выбор действия при решении таких задач.
Например, рассмотрим задачу: «В магазин привезли 6 коробок печенья по 5 килограммов в каждой коробке. Сколько всего печенья привезли в магазин?». В данной задаче рассматриваются две единицы массы печенья – коробки и килограммы. В условии задачи печенье измерено в коробках, а требуется измерить его в килограммах. Причем известно, что в старой единице (коробке) содержится 5 новых (5 кг), т.е. 1 коробка – это 5 кг печенья, а 6 коробок – 6 · 1 кор. = 6 · 5 кг = 6 · (5 · 1кг) = (6 · 5) · 1кг = 30 кг.
4. Деление. Пусть отрезок х состоит из а отрезков, равных е, а отрезок е1 состоит из в отрезков, равных е, то есть mе (х) = а и mе (е1) = в. Выясним, каким числом выражается мера длины отрезка х при единице длины е1.
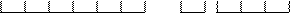 |
х е е1
По условию для отрезков х и е1 можно записать равенства х = а · е и е1 = в · е. Из последнего равенства найдем, что е = е1: в. Подставим найденное значение е в равенство х = а · е, применим правило умножения числа на частное и получим х = а · е = а · (е1: в) = (а: в) · е1. Получившаяся запись означает, что мера длины отрезка х при единице е1 выражается частным чисел а и в.
Таким образом, деление натуральных чисел как мер длин отрезков выражает переход к новой (более крупной) единице длины.
Пусть а = mе (х) и в = mе (е1). Тогда частным натуральных чисел а и в называется натуральное число а: в, равное мере длины отрезка х при новой (более крупной) единице длины е1.
В начальном курсе математики детям встречаются задачи с величинами, в которых рассматривается действие деления. Определение смысла деления натуральных чисел, являющихся значениями величин, позволяет обосновывать выбор действия при решении таких задач.
Рассмотрим задачу: «Вместимость одного пакета для сока 2 л. Сколько потребуется пакетов, чтобы разлить 14 л сока?».
Чтобы решить задачу, изобразим в виде отрезка 14 л и выясним, сколько раз в нем укладывается отрезок, изображающий 2 л. Получаем: 14 л: 2 л/п = 7 (п.).
 |
2л 2л 2л 2л 2л 2л 2л 1л 2л
Можно также и по-другому обосновать решение задачи. В задаче рассматриваются две единицы объема, занимаемого соком, литр и пакет. Так как в задаче требуется результат измерения сока выразить в пакетах, то есть в новой более крупной единице объема, и известно, что в новой единице (пакете) содержится 2 старые (2 л), то 1 л = 1 п.: 2.
14 л = 14 · 1 л = 14 · (1 п.: 2) = (14: 2) ·1 п. = 7 · 1 п. = 7 п.
Задания для самостоятельной работы
1. Приведите примеры множеств, равномощных: а) множеству пальцев на руке; б) множеству окон в аудитории, где проходят занятии по математике; в) множеству студентов в вашей группе; г) множеству страниц в школьной тетради.
2. Соедините следующие пары множеств знаком =, если они равны, и знаком ~, если они равномощны: а) Х – множество сторон квадрата, У – множество углов квадрата; б) Х – множество цифр числа 132, У – множество коэффициентов многочлена 2 х 2 + 3 х + 1; в) Х – множество букв в слове «мир», У = {и, р, м}; г) Х – множество колец на пне дерева, У – множеств лет, прожитых деревом; д) Х – множество страниц в тонкой школьной тетради, У = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
3. Используя теоретико-множественную трактовку суммы натуральных чисел, покажите, что 1) 2 + 5 = 7; 2) 4 + 6 = 10.
4. Объясните, почему первая задача решается сложением, а вторая – вычитанием: 1) У Коли 7 марок, а у Саши на 3 марки больше, чем у Коли. Сколько марок у Саши? 2) В саду посадили 6 вишен, а яблонь на 2 меньше. Сколько посадили яблонь?
5. Найдите значения выражений и объясните, какими законами сложения вы пользовались при вычислении:
1) (57 + 68 + 89) + (11 + 32 + 43) 2) 36 + 72 + 34 + 28
6. Используя теоретико-множественную трактовку отношений «равно» и «меньше», покажите, что 4 = 4, 3 < 6.
7. Используя теоретико-множественную трактовку разности натуральных чисел, покажите, что 1) 8 - 5 = 3; 2) 7 - 1 = 6.
8. Какими способами можно вычислить значения выражений: 1) 11 – (3 + 1); 2) (8 + 7) – 5?
9. Используя теоретико-множественную трактовку умножения натуральных чисел, покажите, что 1) 6· 5 = 30; 2) 7 · 1 =7.
10. Используя теоретико-множественную трактовку деления натуральных чисел, покажите, что 1) 12: 2 = 6; 2) 6: 1 = 6.
11. Найдите значения выражений рациональным способом и объясните, какие законы умножения натуральных чисел были при этом использованы: 1) 4 · 14 · 25; 2) 4 · 8 · 9 · 5 · 5; 3) (15 + 45) · 7; 4) 68 · 13.
12. Вычислите значение частного двумя способами:
а) 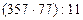 ; б)
; б) 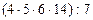 ; в)
; в) 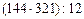 ; г)
; г) 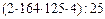
13. Найдите в каждой паре значение второго выражения, используя значение первого:
а) 450: 90 450: (90: 5) б)480: 60 480 6 (60: 10)
14. Объясните, почему первая задача решается умножением, а вторая – делением: 1) На каждую из четырех тарелок положили по 3 апельсина. Сколько всего апельсинов положили? 2) Из 18 роз изготовили 6 одинаковых букетов. Сколько роз получилось в каждом букете?
15. Какими свойствами числового ряда неявно пользуются дети при выполнении следующих заданий: 1) Назови соседей числа 5; 2) Назови самое маленькое натуральное число.
16. При измерении различных величин получили 7 м, 7 см2, 7 кг, 7 мин. Какие величины измеряли? Что показывает в каждом случае число 7?
17. Обоснуйте выбор действия при решении каждой из задач:
1) С первой грядки собрали 5 кг моркови, а со второй – 7 кг. Сколько всего килограммов моркови собрали?
2) От мотка проволоки длиной в 20 м отрезали сначала 7 м проволоки, а затем еще 3 м. Сколько метров проволоки осталось в мотке?
3) Для кафе привезли 15 пакетов вишневого сока по 2 литра в каждом. Сколько всего литров сока привезли в кафе?
4) Масса шести банок варенья равна 12 кг. Какова масса одной банки?
5) У Коли было 6 марок, а у Васи – на 2 марки меньше, чем у Коли. Сколько марок было у Коли?
6) На верхней полке 9 книг, их на 4 книги больше, чем на нижней полке. Сколько книг на нижней полке?
7) Оля прочитала в первый день 8 страниц книги, а во второй день – в 2 раза больше. Сколько страниц книги прочитала Оля во второй день?
18. Приведите пример такой жизненной ситуации, когда нужно сравнить два отрезка, но нет возможности сделать это непосредственно. Укажите возможные способы сравнения отрезков в приведенном вами примере.
ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ ОМД
(СОРТОВАЯ ПРОКАТКА)
Раздел: Методика выполнения практических расчетов технологических процессов прокатки блюмов и сортовой прокатки на станах ОАО «ОЭМК»
Практикум и методические указания
для студентов обучающихся по направлению
150100 – МЕТАЛЛУРГИЯ
(всех форм обучения)
|
|
|
|
|
Дата добавления: 2015-04-25; Просмотров: 841; Нарушение авторских прав?; Мы поможем в написании вашей работы!