Теоретический материал. Проверка статистических гипотез

Проверка статистических гипотез

Практическая работа № 3

Выборочный метод

Практическая работа № 2

1. Расчет выборочных характеристик:

Расчетная таблица

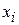
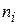
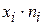
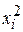
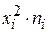
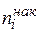
3,2		3,2	10,24	10,24
4,2		25,2	17,64	105,84
5,2			27,04	270,4
6,2		43,4	38,44	269,08
7,2		7,2	51,84	51,84

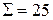
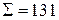
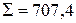
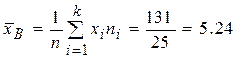(тыс. руб.)

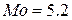(тыс. руб.); 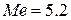(тыс. руб.)

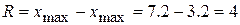(тыс. руб.)

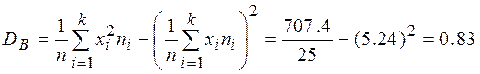
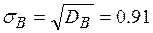(тыс. руб.)

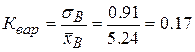
2. Оценка параметров генеральной совокупности:

а) точечные оценки

М (Х)» 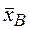, М(Х)» 5,24 (тыс. руб.)

, ,

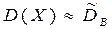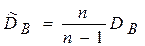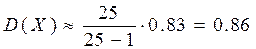
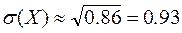, (тыс. руб.)

б) Доверительный интервал для математического ожидания :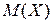

; ; ;

;

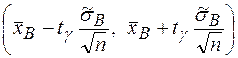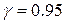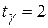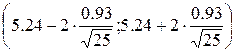Во многих практических задачах возникает необходимость установить теоретический закон распределения случайной величины по опытному (эмпирическому) распределению, представляющему вариационный ряд. Для этого надо определить вид и параметры закона распределения. Вид закона распределения можно предположить, исходя из теоретических предпосылок, графического изображения выборочного распределения и др. Параметры распределения, как правило, неизвестны, их заменяют наилучшими оценками.

Предположим, что известно эмпирическое распределение случайной величины Х, т.е. значения вариант 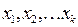и соответствующие им эмпирические частоты .

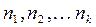Далее, пусть есть основания предположить (выдвинуть гипотезу Н₀), что случайная величина Х распределена нормально. Для проверки этой гипотезы, вычисляются так называемые выравнивающие частоты 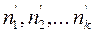(т.е. частоты, которые должны иметь значения признака Х, если он распределен нормально) для тех же объектов, которые попали в выборку.

Между теоретическими и выравнивающими частотами неизбежны расхождения. Случайны ли эти расхождения или выдвинута неверная гипотеза о законе распределения? Для ответа на этот вопрос используются критерии согласия, например, c ² (хи-квадрат) критерий К.Пирсона.

Схема применения c² критерия К.Пирсона:

1. Выдвигаются проверяемая гипотеза Н₀ – признак Х в генеральной совокупности распределен нормально с ,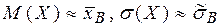

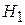– альтернативная гипотеза – признак в генеральной совокупности не распределен нормально.

2. Рассчитывается наблюдаемое значение 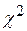критерия К.Пирсона:

,

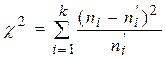где 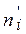– выравнивающие частоты 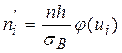, n – объем выборки,

h – разность между двумя соседними вариантам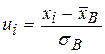и,

и .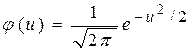

3. По таблице значений 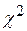для заданного уровня значимости a и числа степеней свободы s (s=k-m-1, k -число различных вариант, m – число параметров распределения) находится c² _кр. Уровень значимости a представляет собой вероятность, при которой о событии (c²>c² _кр), имеющем вероятность a, можно с большой уверенностью сказать, что в единичном испытании оно не произойдет.

4. При c²>c² _кр гипотеза Н₀ отвергается, при c²£c² _кр гипотеза Н₀ не противоречит опытным данным.

Вопросы для подготовки к выполнению и защите работы:

1. Дать определение статистической гипотезы.

2. Описать общую схему проверки статистических гипотез.

3. Дать определение статистического критерия, уровня значимости критерия..

4. Описать схему проверки гипотезы о нормальном распределении изучаемого признака в генеральной совокупности.

5. Записать формулу 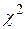критерия согласия Пирсона, указать его статистический смысл.

6. Указать смысл эмпирических, теоретических частот.

Задание к работе:

По данным, полученным в работах №1, 2, проверить гипотезу о нормальном распределении изучаемого признака в генеральной совокупности. Для этого:

1. Сформулировать нулевую и альтернативную гипотезы.

2. Рассчитать теоретические частоты и наблюдаемое значение 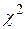критерия согласия Пирсона (значения функции 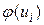определить из таблицы значений плотности вероятности для нормированного нормального закона распределения).

3. По таблице определить критическое значение 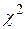критерия согласия Пирсона (уровень значимости 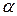принять равным 0,05).

4. Сравнить наблюдаемое и критическое значение 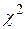критерия согласия Пирсона, сделать вывод о принятии (непринятии) проверяемой гипотезы.

5. Построить графики эмпирического и теоретического распределения.

6. Сделать вывод по работе.

Пример выполнения практической работы № 3 в Excel:

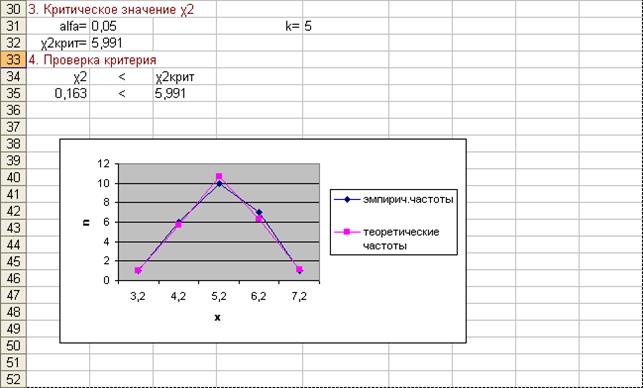
Пример оформления отчета по работе № 3 в тетради:

Дата добавления: 2015-04-25