
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретический материал. Дисперсионный анализ
|
|
|
|
Дисперсионный анализ
Практическая работа № 6
Ряды динамики
Практическая работа № 5
Исходные данные:
Имеются данные о численности зарегистрированных преступлений (в тыс.)
| Год | |||||
| Зарег. преступлений | 13.3 | 13.5 | 14.8 | 16.1 | 16.1 |
1. Ряд динамики – интервальный ряд абсолютных величин.
2. Расчет характеристик ряда динамики:
| Показа-тель времени | Уровень ряда динамики, тыс. | Абсолютный прирост, нат.ед. | Темп роста, % | Темп прироста, % | Абс. значение 1% прироста, тыс. | |||
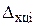
| 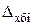
| 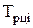
| 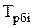
| 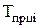
| 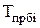
| |||
 2000 2000
| 13,3 13,5 14,8 16,1 16,6 | - 0,2 1,3 1,3 0,5 | - 0,2 1,5 2,8 3,3 | - 101,5 109,6 108,8 103,1 | - 101,5111,3 121,1 124,8 | - 1,5 9,6 8,8 3,1 | - 1,5 11,3 21,1 24,8 | - 0,133 0,135 0,148 0,161 |
Среднее значение уровня ряда:
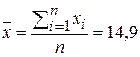 (тыс.)
(тыс.)
3. Расчет линейной модели:
| Год | Уровень ряда 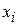
|  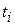
| 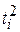
| 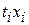
| 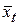
|
| 13,3 13,5 14,8 16,1 16,6 | -2 -1 | -26,6 -13,5 16,1 33,2 | 13,02 13,94 14,86 15,78 16,70 | ||
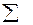
| 74,3 | 9,2 | 74,3 |

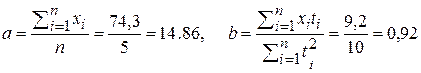
Уравнение тренда имеет вид:
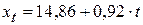

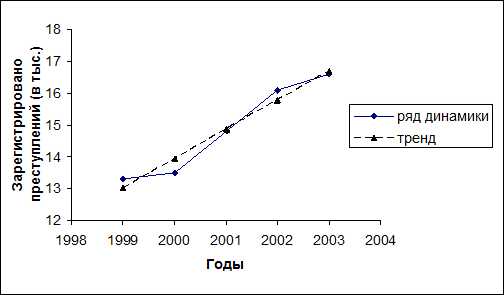
4. Прогноз:
2004 г.: 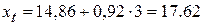 тыс. преступлений
тыс. преступлений
2005 г.: 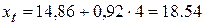 тыс. преступлений
тыс. преступлений
Дисперсионный анализ – это статистический метод, предназначенный для оценки влияния различных факторов на результат, а также для последующего планирования экспериментов. По числу факторов, влияние которых исследуется, различают однофакторный и многофакторный дисперсионный анализ.
Схема применения однофакторного дисперсионного анализа:
1.Данные выборки группируются по признаку, влияние которого оценивается.
2.Выдвигается гипотеза Н0 – нет влияния группирующего Фактора на результат.
3.По данным выборки рассчитываются так называемые межгрупповая 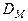 , внутригрупповая
, внутригрупповая 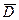 и общая
и общая 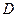 дисперсии. Общая дисперсия отражает вариацию признака за счет всех причин и условий, действующих в выборке. Внутригрупповая дисперсия рассчитывается как средняя из групповых; последние, в свою очередь, отражают вариацию признака за счет условий и причин, действующих внутри групп. Межгрупповая дисперсия характеризует вариацию результативного признака за счет группирующего признака. Сравнивая между собой межгрупповую и внутригрупповую дисперсии, по величине их отношения судят, насколько сильно проявляется влияние группирующего фактора (в этом сравнении и заключается основная идея дисперсионного анализа).
дисперсии. Общая дисперсия отражает вариацию признака за счет всех причин и условий, действующих в выборке. Внутригрупповая дисперсия рассчитывается как средняя из групповых; последние, в свою очередь, отражают вариацию признака за счет условий и причин, действующих внутри групп. Межгрупповая дисперсия характеризует вариацию результативного признака за счет группирующего признака. Сравнивая между собой межгрупповую и внутригрупповую дисперсии, по величине их отношения судят, насколько сильно проявляется влияние группирующего фактора (в этом сравнении и заключается основная идея дисперсионного анализа).
4.Рассчитывается наблюдаемое значение критерия Фишера-Снедекора
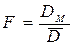 .
.
5.По таблице находится 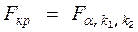 , где
, где 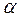 - уровень значимости,
- уровень значимости, 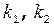 - число степеней свободы.
- число степеней свободы.
6. 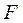 и
и 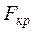 сравниваются:
сравниваются:
- при 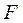 >
> 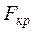 гипотеза отвергается (есть влияние группирующего фактора на результат);
гипотеза отвергается (есть влияние группирующего фактора на результат);
- при 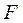 £
£ 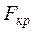 гипотеза принимается (нет различия между группами, нет влияния группирующего фактора на результат).
гипотеза принимается (нет различия между группами, нет влияния группирующего фактора на результат).
Расчет межгрупповой, внутригрупповой, общей дисперсий.
Пусть данные разбиты на m групп по n в группе:
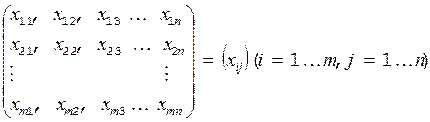
Рассчитаем межгрупповую 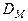 , внутригрупповую
, внутригрупповую 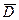 и общую
и общую 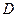 дисперсии. Удобнее сначала подсчитать суммы квадратов отклонений значений признака от соответствующих средних, а затем эти суммы поделить на число степеней свободы; тем самым мы получим значения исправленных выборочных дисперсий, которые и входят в выражение для критерия Фишера. Выражения для сумм квадратов отклонений и чисел степеней свободы приведены в таблице 10.
дисперсии. Удобнее сначала подсчитать суммы квадратов отклонений значений признака от соответствующих средних, а затем эти суммы поделить на число степеней свободы; тем самым мы получим значения исправленных выборочных дисперсий, которые и входят в выражение для критерия Фишера. Выражения для сумм квадратов отклонений и чисел степеней свободы приведены в таблице 10.
Таблица 10.
| Компоненты дисперсии | Сумма квадратов отклонений | Число степеней свободы |
| Межгрупповая | 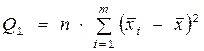
| 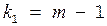
|
| Внутригрупповая | 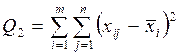
| 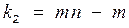
|
| Общая | 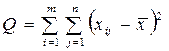
| 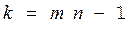
|
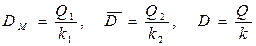 .
.
Вопросы для подготовки к выполнению и защите работы:
1. Дать определение дисперсионного анализа.
2. Записать правило сложения дисперсий, указать его статистический смысл.
2. Описать схему проверки статистической гипотезы о влиянии группирующего фактора на результат эксперимента (схему дисперсионного анализа).
3. Записать формулу критерия Фишера, указать его статистический смысл.
Задание к работе:
По имеющимся данным провести анализ влияния группирующего фактора на изучаемый показатель. Для этого:
1. Сформулировать нулевую и альтернативную гипотезы.
2. Рассчитать наблюдаемое значение 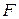 критерия Фишера.
критерия Фишера.
3. По таблице определить критическое значение 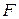 критерия Фишера (уровень значимости
критерия Фишера (уровень значимости 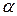 принять равным 0,05).
принять равным 0,05).
4. Сравнить наблюдаемое и критическое значение 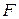 критерия, сделать вывод о принятии (непринятии) проверяемой гипотезы.
критерия, сделать вывод о принятии (непринятии) проверяемой гипотезы.
5. Сделать вывод по работе.
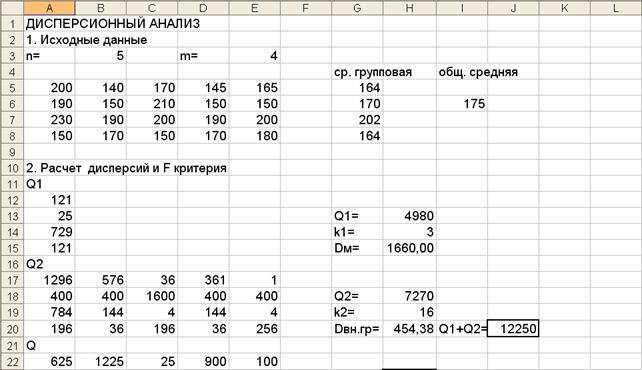
Пример выполнения практической работы № 6 в Excel:

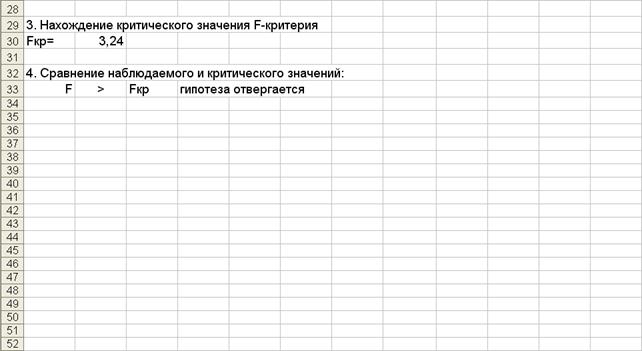
Пример оформления отчета по работе № 6 в тетради:

|
|
|
|
|
Дата добавления: 2015-04-25; Просмотров: 303; Нарушение авторских прав?; Мы поможем в написании вашей работы!