Свойства. · Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:

· Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:

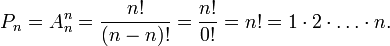
· Композиция определяет операцию произведения на перестановках одного порядка: 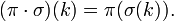Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают .

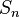· Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент сопоставляется с перестановкой 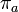, задаваемой тождеством 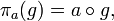где g — произвольный элемент группы G, а — групповая операция.

19) ПодстановкиПусть M -- некоторое множество. Подстановкой на M назовем взаимно однозначное отображение $a:M\rightarrow M$ множества M на себя. Обозначим через S(M) множество всех подстановок на M. Группа подстановокПусть a и b -- две подстановки из S(M). Назовем произведением ab этих подстановок композицию отображений a, b, то есть ab -- такой элемент из S(M), что m(ab)=(ma)b для всех $m\in M$Теорема. Множество S(M) является группой относительно введенной операции умножения, то есть в S(M) есть единичный элемент e со свойством: ex=xe=x для любого $x\in S(M)$; для любого $x\in S(M)$ есть $y\in S(M)$, что xy=yx=e, и операция умножения ассоциативнаДоказательство. Нам необходимо проверить три аксиомы. В S(M) имеется единичный элемент -- это тождественное отображение, которое обозначим буквой e. Известно также, что для всякого взаимно однозначного отображения x множества M на M существует обратное отображение x-1, для которого xy=yx=e. Осталось проверить аксиому ассоциативности. Пусть a, b, c -- подстановки из $S(M),\ m$ -- элемент множества M. Вычисляя образ элемента m при отображениях (ab)c и a(bc), мы убеждаемся, что эти отображения совпадают:m((ab)c)=(m(ab))c=((ma)b)c,m(a(bc))=(ma)(bc)=((ma)b)c.

20)

Дата добавления: 2015-04-25