Разработка алгоритма деления

В прямых кодах удобнее делить модули чисел. Знак результата не зависит от соотношения модулей делимого и делителя и определяется по выражению 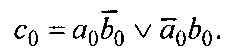(4.1).

(4.1)

Деление чисел с фиксированной запятой в заданном формате невозможно, если модуль делимого не меньше модуля делителя. Поэтому сначала следует проверить соотношение операндов путем вычитания делителя из делимого. Если разность окажется положительной, то можно формировать признак переполнения OV= 1 и завершать операцию. В противном случае модуль частного оказывается меньше 1, т.е. переполнение отсутствует и деление возможно.

Алгоритмы деления с восстановлением остатка и без восстановления остатка подробно рассмотрены в разд. 3.9. Учитывая приведенный там сравнительный анализ алгоритмов, выберем метод деления без восстановления остатка.

ГСА деления без восстановления остатка представлена на рис. 4.3. Алгоритм предусматривает формирование знака результата согласно формуле (4.1) и сохранение его временно в переменной s. После этого производится деление модулей чисел (знаки операндов обнуляются).

(Страница93)

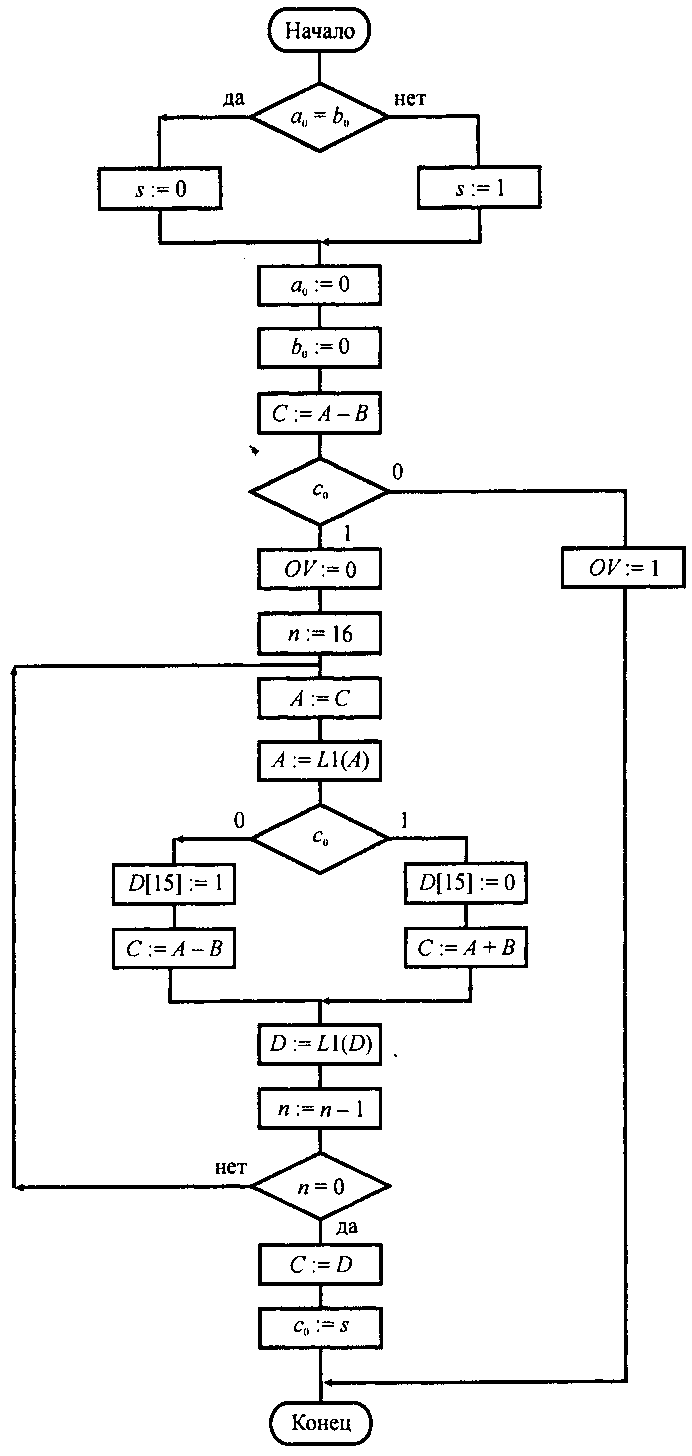
Рис. 4.3. Граф-схема алгоритма деления

Сначала производится пробное вычитание делителя из делимого. Поскольку знаки операндов — 0, то появление 1 в знаковом разряде разности означает, что A<B, и можно продолжать деление (целая часть частного равна 0).

При с₀= 0 деление невозможно — формируется признак переполнения.

В процессе получения цифр частного значение очередного остатка принимает переменная С. Независимо от знака остатка она копируется в переменную А, которая затем увеличивается вдвое путем сдвига влево на один разряд. В зависимости от знака переменной C (знака остатка) формируется очередная цифра переменной D (частного) и принимается решение о действии на следующем шаге — добавлять или вычитать делитель из сдвинутого остатка. После арифметической операции выполняется сдвиг влево частного D (освобождается место для очередной цифры частного), изменяется счетчик цифр частного и проверяется условие выхода из цикла — получение шестнадцати цифр частного, включая самую первую цифру — "0 целых", на место которой копируется знак частного из переменной s.

Дата добавления: 2015-04-25