Векторы и матрицы

Множества

Множество — это совокупность элементов произвольной природы. Например, множество правовых норм, множество субъектов права, множество органов государства и т. д.

Понятие множества, взятое во всей его общности, лежит в основе всех разделов математики.

Символическое обозначение (конечного) множества:

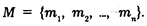
Множество А, составленное из некоторого числа элемен-. тов множества В, называется подмножеством множества А.

Объединение множества — математическая операция, заключающаяся в образовании из двух данных некоторого но­вого множества, каждый элемент которого принадлежит либо первому, либо второму множеству. Обозначение данной опе­рации:

Р = А È В.

Произведение (пересечение) множеств — математическая операция образования из двух данных множеств А и В некото­рого нового множества Q, каждый элемент которого принад­лежит множествам A и В одновременно. Обозначения данной операции:

Q= A Ç В.

Запись x Î X означает: элемент х принадлежит множе­ству X.

Запись Х Ì Y означает: множество Х является подмноже­ством некоторого множества Y.

Вектор — упорядоченный набор элементов некоторого множества.

Вектор обозначается так:

Например, вектором является набор признаков, взятых всегда в определенном числе и последовательности.

Каждый признак этого набора называется компонентой вектора.

Горизонтально расположенный вектор называется вектор-строкой.

Вертикально расположенный вектор называется вектор-столбцом.

Векторы с числовыми компонентами можно складывать или умножать на числа.

Любой вектор можно рассматривать как разновидность более сложного математического объекта — матрицы. Матри­цей называется прямоугольная таблица чисел, имеющая сле­дующий вид:

В этой матрице буквы а_ij означают какие-то числа или иные символы, а т и n всегда являются целыми числами: т обозначает число строк в данной матрице, а n — число столб­цов.

Как и векторы, матрицы можно складывать и умножать на число.

Дата добавления: 2015-04-25