Аффинные преобразования, их свойства, однородные координаты

Представление геометрических моделей. Полигональные сетки.

Наиболее распространённые представления графических объектов:

1. Пространственное подразбиение.

Если в трёхмерном пространстве есть тело, то это пространство можно разбить на кубики (воксели). Для каждого кубика b(i, j, k) можно указать, пересекается ли он с телом, то есть лежит ли он внутри, на границе – 1 или вне тела – 0. В некоторых случаях удобно применять некоторые промежуточные значения, задавая тем самым плотность в данной точке пространства.

Характеристики воксельного представления:

• Только приближение реального объекта. Поверхности, не параллельные осям координат, представляются приблизительно. Качество приближения зависит от относительного размера вокселей.

• Требует больших размеров памяти для хранения, и эти требования резко возрастают при увеличении разрешения (растет как куб от разрешения).

• С таким представлением хорошо работают в основном пространственные алгоритмы, такие как вычисление объема объекта, нахождение центра масс и т.д.

• Можно проводить набор операций: пересечение, объединение, вычитание. 2. Граничное (поверхностное). Тела задаются ограниченными фрагментами поверхностей.

3. Конструктивное.

При конструктивном представлении вводятся примитивы тел. Конструируя эти объекты и применяя теоретико-множественные операции, можно получить более сложное тело.

Под операциями понимаются булевы операции над примитивами, а так же геометрические преобразования, такие как передвижение, поворот, изменение размеров.

Полигональная сетка представляет собой совокупность ребер, вершин и многоугольников.

Для решения таких задач, как движение объектов и их частей, управления камерой применяются аффинные преобразования (АП), рассмотрим их основные свойства:

1) точки, лежащие на одной прямой, после преобразования лежат на одной прямой;

2) пересекающиеся прямые остаются пересекающимися, а параллельные – параллельными;

3) при АП пространства пересекающиеся плоскости остаются пересекающимися, параллельные – параллельными, а скрещивающиеся – скрещивающимися;

4) при АП сохраняются отношения площадей двух квадратов на плоскости и отношение объемов двух кубов в пространстве.

Пусть М - произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы. Однородными координатами этой точки называется любая тройка одновременно неравных нулю чисел x₁, x₂, x₃, связанных с заданными числами x и y следующими соотношениями:

x₁/x₃=x, x₂/x₃=y.

При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М (х, у) плоскости ставится в соответствие точка М *(х, у,1) в пространстве. Произвольная точка на прямой, соединяющей начало координат, точку 0 (0, 0, 0) с точкой М *(х, у, 1), может быть задана тройкой чисел вида (hx, hy, h).

Будем считать, что h ¹0. Вектор с координатами hx, hy, h является направляющим векто­ром прямой, соединяющей точки 0 (0, 0, 0) и М *(х, у, 1). Эта прямая пересекает плоскость z = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) коорди­натной плоскости ху.

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости. В самом деле, считая h = 1, сравним две записи: помеченную символом * и матричную:

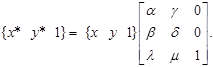
Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство 1 == 1. Тем самым сравниваемые записи можно считать равносильными.

Выпишем соответствующие матрицы третьего порядка для базовых аффинных преобразований:

1. Матрица вращения (rotation) 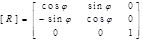;	2. Матрица растяжения (сжатия) (dilatation) ;
3. Матрица переноса (translation) ;	4. Матрица отражения (reflection)

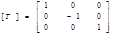
Дата добавления: 2015-03-29