Аффинные преобразования на плоскости

Допустим, на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 1). Вводя на плоскости еще одну прямолинейную систему координат,мы ставим в соответствие тойже точке М другую пару чисел - (х*, у*).

Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями:

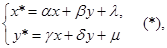где a, b, l, g, m, d – произвольные числа, связанные неравенством

Формулы (*) можно рассматривать двояко: либо сохраняется точка и изменяется координатная система (рис. 2) – в этом случае произвольная точка М остается той же, изменяются лишь ее координаты, либо изменяется точка и сохра­няется координатная система (рис. 3) – формулы (*) задают отображение, переводящее произвольную точку M(x,y) в точку М*(х*, у*), координаты которой определены в той же координатной системе.

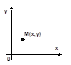Рис. 1

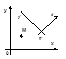Рис. 2

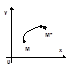Рис. 3

В дальнейшем мы будем рассматривать формулы (*) как правило, согласно которому в заданной системе прямолинейных координат преобразуются точки плоскости.

В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев. При исследовании геометрического смысла числовых коэффициентов в формулах (*) для этих случаев нам удобно считать, что заданная система координат является прямоугольной декартовой.

1. Поворот вокруг начальной точки на угол j описывается формулами:

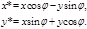
2. Растяжение (сжатие) вдоль координатных осей можно задать так:

х* = aх, у*=dу, а > 0, d > 0.

Например, растяжение (сжатие) вдоль оси абсцисс обеспечивается при условии, что

a > 1 (0 < a < 1).

3. Отражение (относительно оси абсцисс) задается при помощи формул:

х* = х, у* = -у.

4. Параллельный перенос обеспечивают соотношения

x* = x + l,

у* = у + m..

Выбор этих четырех частных случаев определен двумя обсто­ятельствами.

1. Каждое из приведенных преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наде­лены и постоянные числа, входящие в приведенные формулы).

2. Любое преобразование вида (*) всегда можно представить в виде последовательного исполнения простейших преобразований.

Для эффективного использования этих известных формул более удоб­ной является их матричная запись.

, ,

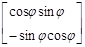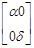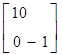
Этого можно достичь, например, так: перейти к опи­санию произвольной точки плоскости тройкой чисел.

Дата добавления: 2015-03-29