Удобна показательная форма записи

При умножении или делении комплексных чисел

Удобно использовать алгебраическую форму записи

При суммировании комплексных чисел

Например,

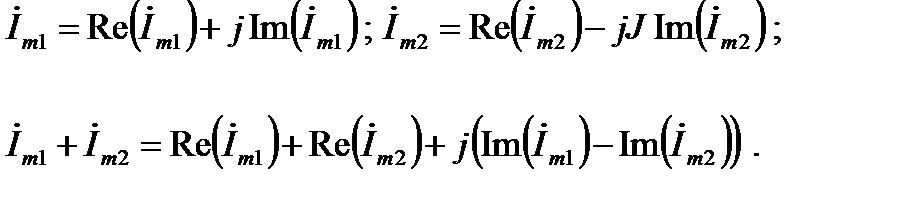
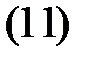
Например,

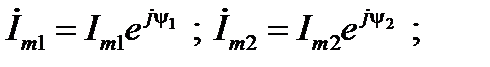
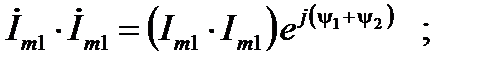
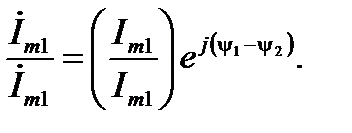(12)

Если далее необходимо производить суммирование, то результаты (12) нужно представить в алгебраической форме, как указано в (8). Для этого существуют соотношения, определяющие переход от одной формы записи в другую. Например, имеем показательную форму представления комплексного числа

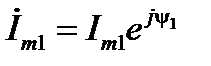, (13)

тогда компоненты алгебраической формы записи находятся так (см. рис. 4)

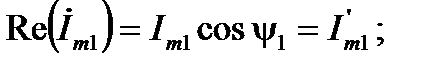
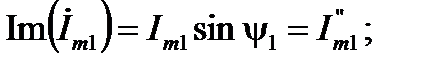(14)

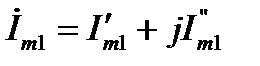. (15)

Необходимо помнить, что знак составляющих комплексного числа зависит от величины и знака угла 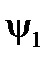. Если комплексный вектор задан в алгебраической форме

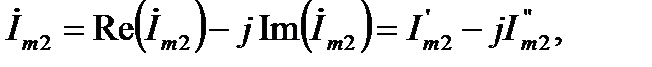(16)

тогда модуль 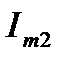и аргумент 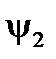, как компоненты показательной формы записи, найдутся (см. рис.4)

;

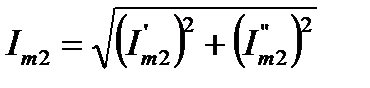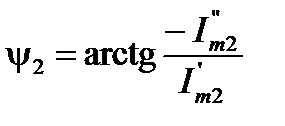. (17)

Здесь также величина и знак 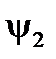определяется знакам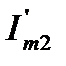и и 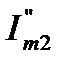. Отметим некоторые особенности и элементарные свойства комплексных чисел. В соответствии с соотношением Эйлера:

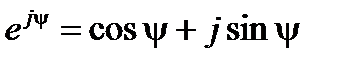(18)

имеем

;

;

;

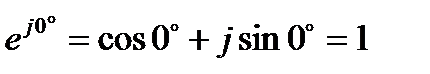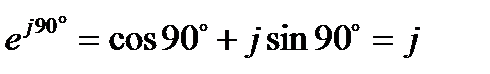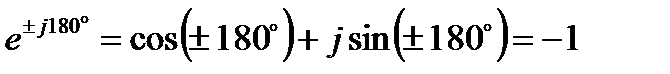; (19)

;

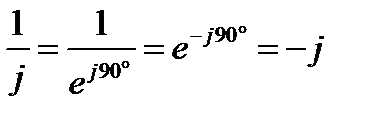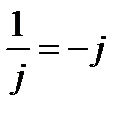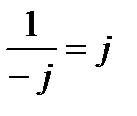; ; (20)

; ; .

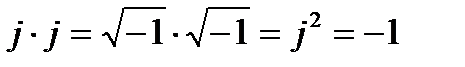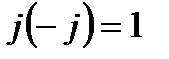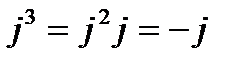Итак, любую синусоидальную функцию можно однозначно изобразить вектором на комплексной плоскости, который в свою очередь может быть однозначно выражен соответствующим ему комплексным числом. Очевидно, что это комплексное число является некоторым условным выражением исходной синусоидальной функции времени. Модуль комплексного числа, изображающего синусоидальную функцию времени равен её амплитуде, а аргумент – начальной фазе.

Дата добавления: 2015-05-06