Методический материал

Программа работы

ИССЛЕДОВАНИЕ СХЕМ КОМБИНАЦИОННОЙ И ПОСЛЕДОВАТЕЛЬНОЙ ЛОГИКИ

Лабораторная работа № 8

1. Исследование схем комбинационной логики

1.1. Снять и построить диаграмму работы элемента НЕ. Составить его таблицу истинности.

1.2. Снять и построить диаграмму работы элемента ИЛИ-НЕ. Составить его таблицу истинности.

1.3. Снять и построить диаграмму работы элемента ИЛИ. Составить его таблицу истинности.

1.4. Снять и построить диаграмму работы элемента И-НЕ. Составить его таблицу истинности.

1.5. Снять и построить диаграмму работы элемента И. Составить его таблицу истинности.

2. Исследование схем последовательной логики

2.1. С использованием логических элементов И-НЕ собрать схему асинхронного RS-триггера с прямыми входами. Снять и построить диаграмму его работы, составить таблицу переходов.

2.2. С использованием логических элементов ИЛИ-НЕ собрать схему асинхронного RS-триггера с инверсными входами. Снять и построить диаграмму его работы, составить таблицу переходов.

2.3. С использованием логических четырех элементов ИЛИ-НЕ собрать схему тактируемого D-триггера. Снять и построить диаграмму его работы.

а

б

в

г

д

Рисунок 8.1

Логический элемент ИЛИ имеет несколько входов и один общий выход. Его условное обозначение показано на рис.8.1а. Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкции):

F = x₁ + x₂ + x₃ + … + x_n,

где F – функция; x₁, x₂, x₃, …, x_n – аргумент (переменные, двоичные сигналы на входах).

Здесь функция F = 0, когда все его аргументы равны нулю, и F = 1 при одном, нескольких или всех аргументах, равных единице.

На практике возможны случаи, когда число входов используемого логического элемента ИЛИ превышает количество входных сигналов. Неиспользованные входы заземляют. Тем самым исключая возможность прохождения помех через элемент ИЛИ от наводок по неиспользованным входам.

Логический элемент И имеет несколько входов и один общий выход. Его условное обозначение показано на рис.8.1б. Логический элемент И выполняет операцию логического умножения (конъюнкции):

F = x₁ · x₂ · x₃ · … · x_n,

где F – функция; x₁, x₂, x₃, …, x_n – аргумент (переменные, двоичные сигналы на входах).

Здесь функция F = 0, когда хотя один из его аргументов равен нулю, и F = 1 при всех аргументах, равных единице.

В случае применения логического элемента И, имеющего число входов, больше количествавходных сигналов, неиспользованные входы элемента соединяют с шиной “+” источника питания (подают сигнал логической “1”). Это уменьшает вероятность прохождения помех на выход элемента И от наводок по неиспользованным.

Логический элемент НЕ имеет один вход и один выход. Его условное обозначение показано на рис.8.1в. Элемент НЕ выполняет операцию инверсии (отрицания), в связи с чем его называют логическим инвертором. Им реализуется функция

.

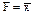Сигналу x = 0 на входе соответствует F = 1 и, наоборот, при x = 1 F = 0.

Условное обозначение элемента ИЛИ-НЕ показано на рис.8.1г. Он объединяет элементы ИЛИ и НЕ с показанной очередностью проведения операций. В связи с этим входным сигналам, равным единице, соответствует логический “0” на выходе, а при нулевых сигнала на всех входах F = 1.

Функциональная операция, выполняемая элементом ИЛИ-НЕ при n входах, определяется выражением

.

Условное обозначение логического элемента И-НЕ и эквивалентная структурная схема показаны на рис.8.1д. Логической “1” на всех информационных входах соответствует логический “0” на выходе элемента. При логическом “0” на одном из входов создается логическая “1” на выходе. Логическая функция элемента И-НЕ при n входах отвечает выражению

.

В импульсной цифровой технике широко используются функциональные узлы, способные сохранять двоичную информацию (состояния “0”, “1”) после окончания действия входных импульсов. Такие функциональные узлы называются триггерами. Указанное свойство триггера обусловлено тем, что факторами, воздействующими на его состояние, являются не только внешние управляющие сигналы, но и сигналы самого триггера (сигналы обратной связи).

Триггеры отличают функциональный признак, определяющий поведение триггера при воздействие сигнала управления (R-S, D, T, J-K и др.), а также используемый способ управления (асинхронные и тактируемые). В асинхронных триггерах переключение из одного состояния в другое осуществляется непосредственно с поступлением сигнала на информационный вход. В тактируемых триггерах помимо информационных входов имеется вход тактовых импульсов, их переключение производится только при наличие разрешающего, тактирующего импульса.

На рис.8.2а показана структурная схема асинхронного R-S-триггера на логических элемента И-НЕ. Схема имеет два выхода 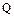- прямой, 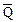- инверсный. Асинхронный R-S триггер, как и триггер любого другого типа, характеризуется двумя состояниями: логический “1” и логического “0”. Состоянию логической “1” соответствует 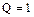, ; состоянию логического “0” - , .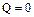

По информационному входу 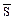производится установка триггера в состояние логической “1”, по входу - установка (перевод) триггера в исходное состояние логического “0”. Этому соответствуют сокращенные обозначения входов и название триггера: S – set (установка), R – reset (возвращение в исходное состояние).

Принцип действия триггера определяется поведением в нем элементов И – НЕ. Он иллюстрируется таблицей переходов триггера, где указаны значение входных сигналов 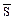и в некоторый момент времени tⁿ и состояние триггера (по значению его прямого выхода) в следующий момент времени tⁿ⁺¹ после прихода очередных импульсов.

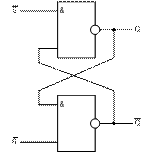
На рис.8.2б приведена структурная схема асинхронного R-S-триггера на логических элемента ИЛИ-НЕ. В отличие от предыдущей схемы триггер управляется не инверсными, а прямыми значениями входных сигналов.

а	б
Рисунок 8.2 – Структурная схема асинхронного R-S-триггера а) - с прямыми; б) - с инверсными входами

D-триггеры имеют один информационный вход. Состоянию логической “1” соответствует единица на входе триггера, логического “0” – нулевой уровень входного сигнала. На практике наибольшее применение получили тактируемые (однотактные и двухтактные) D-триггеры. Их обозначение обусловлено свойством сохранять состояние логической “1” после снятия входного сигнала до прихода очередного тактового импульса (delay - задержка).

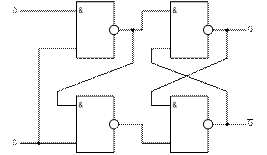
На рис.8.3 приведена структурная схема однотактного D-триггера, выполненного на основе R-S-триггера.

Рисунок 8.3 – Структурная схема тактируемого D-триггера

Дата добавления: 2015-05-06