
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование фазовых соотношений в цепях переменного тока
|
|
|
|
Материалы с малой коэрцитивной силой, меньше 40 А/м называются магнитомягкими материалами.
Вопрос 32
Начальная магнитная проницаемость mн - значение магнитной проницаемости при малой напряженности поля.
Максимальная магнитная проницаемость mmax - максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях.
Из других основных терминов, характеризующих магнитные материалы, отметим следующие.
Намагниченность насыщения - максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля.
Петля гистерезиса - зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения - уменьшение, переход через нуль, после достижения того же значения с обратным знаком - рост и т.п.
Максимальная петля гистерезиса - достигающая максимальной намагниченности насыщения.
Остаточная индукция Bост - индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля.
Коэрцитивная сила Нс - напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
Материалы с большой коэрцититивной силой (более 1000 А/м) называются магнитотвердыми материалами. Они используются в качестве постоянных магнитов.
по дисциплине
«Электротехника»
Выполнил студент 2 курса
группы 11-ББ-ИБ-3
Благочиннов Е.Д.
Проверил:
профессор Тельнов Г.В.
Краснодар
Цель работы:
1. Изучение фазовых соотношений и свойств элементов электрических цепей переменного тока и получение навыков измерения и расчёта их параметров в системе компьютерного моделирования
2. Закрепить и совершенствовать знания применимости законов Ома и Кирхгофа в электрических цепях переменного тока.
3. Привить навыки проведения научных исследований и использования измерительных приборов (осциллографа).
Учебные вопросы:
1. Измерение фазового сдвига между напряжением и током в цепи с чисто реактивной нагрузкой.
2. Измерение фазового сдвига между напряжением и током в RL и RC цепях переменного тока.
3. Измерение параметров разветвлённой цепи переменного тока.
1 Измерение фазового сдвига между напряжением и током в цепи с чисто реактивной нагрузкой
1.1 Измерение фазового сдвига между напряжением и током в ёмкостном элементе цепи
| Канал А (Uвх) |
| Канал А |
| Канал B (Uвых) |
| Канал B |

Рисунок 1.1.1. Схема для измерения сдвига фаз между напряжением и током в цепи из последовательно конденсатора и резистора.
Для нахождения ёмкостного сопротивления конденсатора воспользуемся формулой:
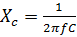 ;
;
(где 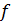 - частота источника, С – ёмкость конденсатора).
- частота источника, С – ёмкость конденсатора).
Для нахождения максимальных значений напряжения подведём курсоры на экране осциллографа к точкам максимума функций, которые выводит осциллограф, представленный на рисунке 1.1.1.
Подводя курсоры осциллографа к точкам перехода от отрицательных значений функции к положительным найдём периоды колебаний напряжения на соответствующих участках.
Временной сдвиг (∆T) найдем, подводя один курсор осциллографа к точке перехода от отрицательных значений к положительным одного графика, а второй курсор подведя к аналогичной точке второго графика, как показано на рисунке 1.1.2. В поле «T2-T1» осциллограф показывает временной сдвиг.
Максимальное значение тока найдём по формуле:
 ;
;
(где UmR – амплитудное значение напряжения на канале B).
Для измерения фазового сдвига воспользуемся формулой:
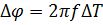
Для теоретического расчёта фазового сдвига воспользуемся формулой
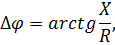
(где X – реактивное сопротивление цепи, R – активное сопротивление цепи).
Применим описанные выше действия для трёх различных параметров электрической цепи и полученные результаты вместе с показаниями измерительных приборов (амперметра и вольтметра) занесём в таблицу 1.1.1.
| ∆T |
| Канал А |
| Канал А (Uвх) |
| Канал B |
| Канал B (Uвых) |
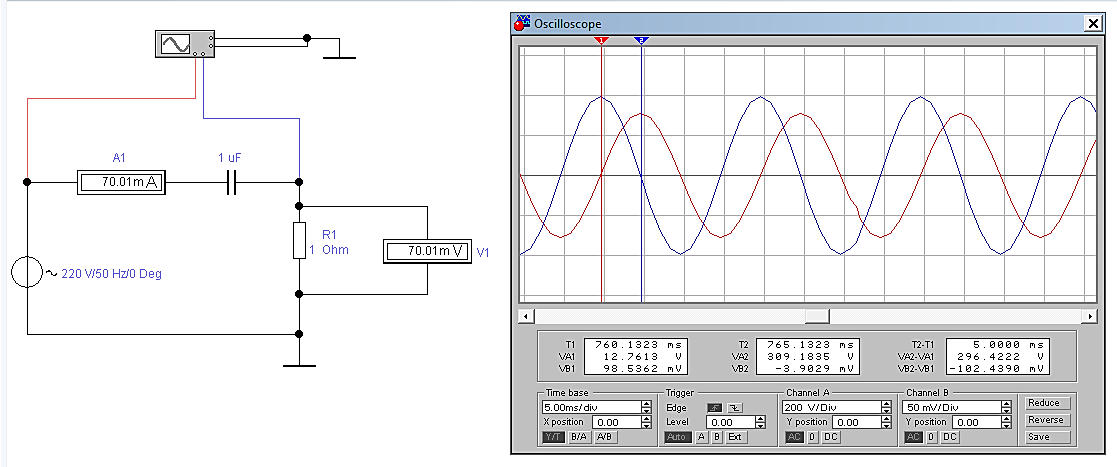
Рисунок 1.1.2. Цепь с параметрами E1= 220 В; f= 50Гц; С= 1мкФ; R= 1 Ом
Для цепи с параметрами E1= 220 В; f= 50Гц; С= 1мкФ; R= 1 Ом


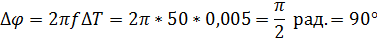

Для цепи с параметрами E1= 220 В; f= 50Гц; С= 100мкФ; R= 1 Ом
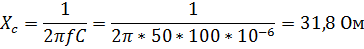

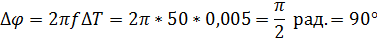
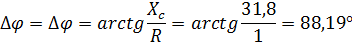
Для цепи с параметрами E1= 220 В; f= 100Гц; С= 1мкФ; R= 1 Ом
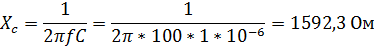


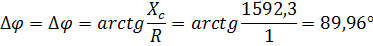
Таблица 1.1.1.
| A1 (А) | V1 (В) | Xc (Ом) | UA=UmC (В) | Ub=UmR (В) | Tu (с) | Ti (с) | ∆T (с) | Im (А) | ∆ 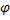 (град.) (град.)
| ||
| измерения | расчёт | ||||||||||
| E1= 220 В; f= 50Гц; С= 1мкФ; R= 1 Ом | |||||||||||
| 0,07 | 0,07 | 3184,7 | 308,3 | 0,1 | 0,02 | 0,02 | 0,005 | 0,1 | 
| ||
| E1= 220 В; f= 50Гц; С= 100мкФ; R= 1 Ом | |||||||||||
| 6,9 | 6,9 | 31,8 | 9,9 | 0,02 | 0,02 | 0,005 | 9,9 | 
| |||
| E1= 220 В; f= 100Гц; С= 1мкФ; R= 1 Ом | |||||||||||
| 0,14 | 0,14 | 1592,3 | 0,19 | 0,01 | 0,01 | 0,0025 | 0,19 | 
| |||
В ходе опыта было установлено, что угол сдвига фаз в цепи с чисто реактивной нагрузкой не зависит от ёмкости конденсатора и практически равен своему теоретическому значению.
1.2 Измерение фазового сдвига между напряжением и током в индуктивном элементе цепи
| Канал А (Uвх) |
| Канал B |
| Канал B (Uвых) |
| Канал А |
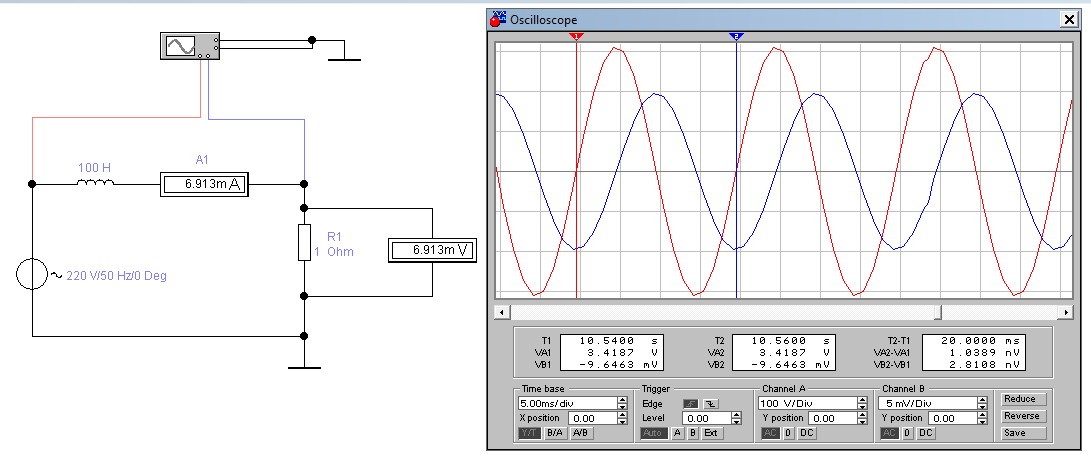 Рисунок 1.2.1. Схема для измерения сдвига фаз между напряжением и током в цепи из последовательно включённых катушки индуктивности и резистора.
Рисунок 1.2.1. Схема для измерения сдвига фаз между напряжением и током в цепи из последовательно включённых катушки индуктивности и резистора.
Параметры цепи рассчитываются аналогично цепи, представленной в
пункте 1.1. Однако в данной цепи необходимо вычислить индуктивное сопротивление, а не ёмкостное.
Индуктивное сопротивление найдём по формуле:
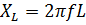
(где L – индуктивность катушки, f – частота источника).
Для теоретического расчёта фазового сдвига воспользуемся формулой
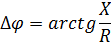
(где X – реактивное сопротивление цепи, R – активное сопротивление цепи).
| ∆T |
| Канал А |
| Канал А (Uвх) |

Применим описанные выше действия для трёх различных параметров электрической цепи и полученные результаты вместе с показаниями измерительных приборов (амперметра и вольтметра) занесём в таблицу 1.2.1.
Соответствующие цепи с подключёнными к ним осциллографами для измерения временного сдвига представлены на рисунках 1.2.2.
| Канал B (Uвых) |
| Канал B |
Для цепи с параметрами E1= 220 В; f= 50Гц; L= 100Гн; R= 1 Ом
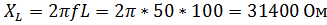
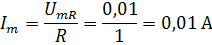
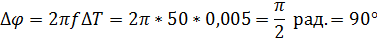
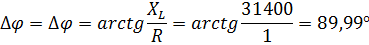
Для цепи с параметрами E1= 220 В; f= 50Гц; L= 1000Гн; R= 1 Ом


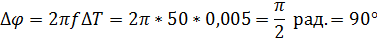
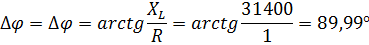
Для цепи с параметрами E1= 220 В; f= 100Гц; L= 10Гн; R= 1 Ом
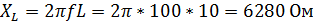
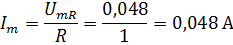

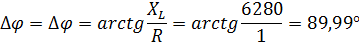
Таблица 1.2.1.
| A1 (А) | V1 (В) | XL (Ом) | UA=UmL (В) | Ub=UmR (В) | Tu (с) | Ti (с) | ∆T (с) | Im (А) | ∆ 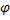 (град.) (град.)
| ||
| измерения | расчёт | ||||||||||
| E1= 220 В; f= 50Гц; L= 100Гн; R= 1 Ом | |||||||||||
| 0,0069 | 0,0069 | 308,7 | 0,01 | 0,02 | 0,02 | 0,005 | 0,01 | 89,99 | |||
| E1= 220 В; f= 50Гц; L= 1000Гн; R= 1 Ом | |||||||||||
| 0,007 | 0,007 | 308,7 | 0,001 | 0,02 | 0,02 | 0,005 | 0,0009 | 89,99 | |||
| E1= 220 В; f= 100Гц; С= 10Гн; R= 1 Ом | |||||||||||
| 0,03 | 0,03 | 309,8 | 0,05 | 0,01 | 0,01 | 0,0025 | 0,048 | 89,99 | |||
В ходе опыта было установлено, что угол сдвига фаз в цепи с чисто реактивной нагрузкой не зависит от индуктивности катушки и практически равен своему теоретическому значению.
2 Исследование фазового сдвига между напряжением и током в RL и RC цепях переменного тока
2.1 Исследование фазового сдвига между напряжением и током в RC цепи переменного тока
| Канал А (Uвх) |
| Канал А |
| Канал B (Uвых) |
| Канал B |

Рис. 2.1.1. Схема для измерения сдвига фаз между напряжением и током в RC цепи
Применим описанные в пункте 1.1 действия для трёх различных параметров электрической цепи и полученные результаты вместе с показаниями измерительных приборов (амперметра и вольтметра) занесём в таблицу 2.1.1.
Соответствующие цепи с подключёнными к ним осциллографами для измерения временного сдвига представлены на рисунках 2.1.2 – 2.1.4.
| ∆T |
 Рисунок 2.1.2. Цепь с параметрами E1= 220 В; f= 50Гц; С= 1мкФ; R= 2 кОм
Рисунок 2.1.2. Цепь с параметрами E1= 220 В; f= 50Гц; С= 1мкФ; R= 2 кОм
| ∆T |
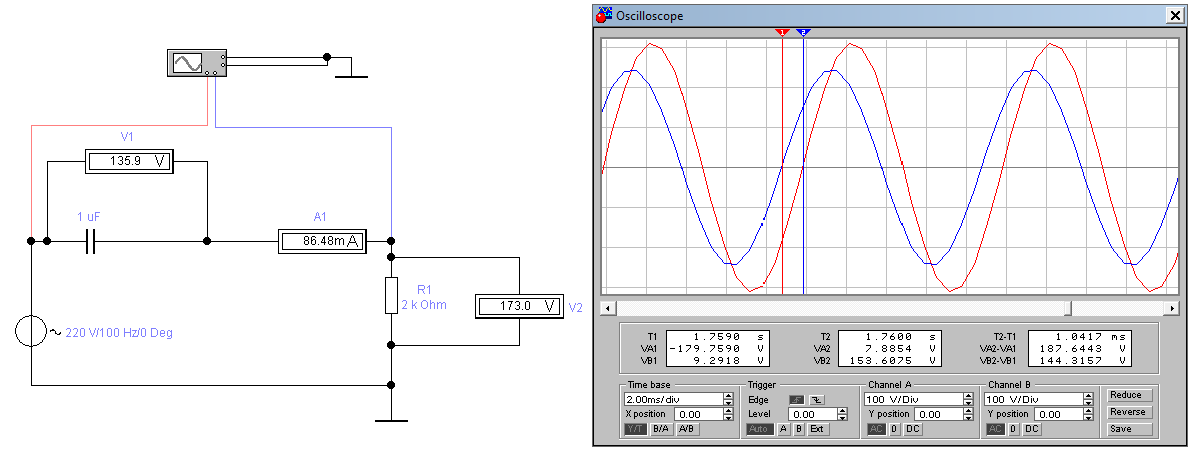
Рисунок 2.1.3. Цепь с параметрами E1= 220 В; f= 100Гц; С= 1мкФ; R= 2 кОм
| ∆T |
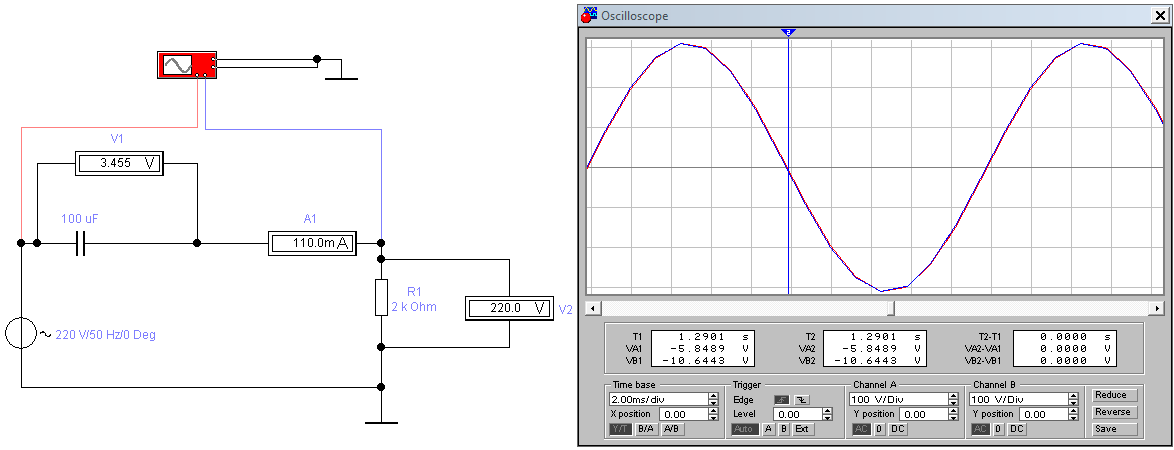 Рисунок 2.1.4. Цепь с параметрами E1= 220 В; f= 50Гц; С= 100мкФ; R= 2 кОм
Рисунок 2.1.4. Цепь с параметрами E1= 220 В; f= 50Гц; С= 100мкФ; R= 2 кОм
Для цепи с параметрами E1= 220 В; f= 50Гц; С= 1мкФ; R= 2 кОм




Для цепи с параметрами E1= 220 В; f= 100Гц; С= 1мкФ; R= 2 кОм
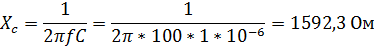
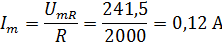

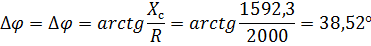
Для цепи с параметрами E1= 220 В; f= 50Гц; С= 100мкФ; R= 2 кОм
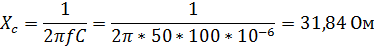


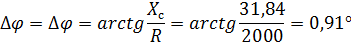
Таблица 2.1.1.
| A1 (А) | V1 (В) | XC (Ом) | UAM (В) | UBM (В) | TA (с) | TB (с) | ∆T (с) | Im (А) | ∆ 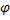 (град.) (град.)
| ||
| измерения | расчёт | ||||||||||
| E1= 220 В; f= 50Гц; С= 1мкФ; R= 2 кОм | |||||||||||
| 0,05 | 185,6 | 
| 309,1 | 165,9 | 0,02 | 0,02 | 0,0032 | 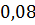
| 57,6 | 
| |
| E1= 220 В; f= 100Гц; С= 1мкФ; R= 2 кОм | |||||||||||
| 0,08 | 1592,3 | 309,7 | 241,5 | 0,01 | 0,01 | 0,001 | 0,12 | 
| |||
| E1= 220 В; f= 50Гц; С= 100мкФ; R= 2 кОм | |||||||||||
| 0,11 | 3,4 | 31,84 | 0,02 | 0,02 | 0,15 | 
| |||||
В ходе опыта было установлено, что угол сдвига фаз в RC цепи зависит как от ёмкости конденсатора, так и от частоты ЭДС источника. Измеренные значения угла сдвига фаз практически равны своему теоретическому значению.
2.2 Исследование фазового сдвига между напряжением и током в RL цепи переменного тока
Составим подключённую к осциллографу электрическую цепь, представленную на рисунке 2.2.1, из последовательно включённых элементов: катушки индуктивности и резистора. Подключим эту цепь к идеальному источнику однофазной ЭДС.
| Канал А |
| Канал А (Uвх) |
| Канал B |
| Канал B (Uвых) |
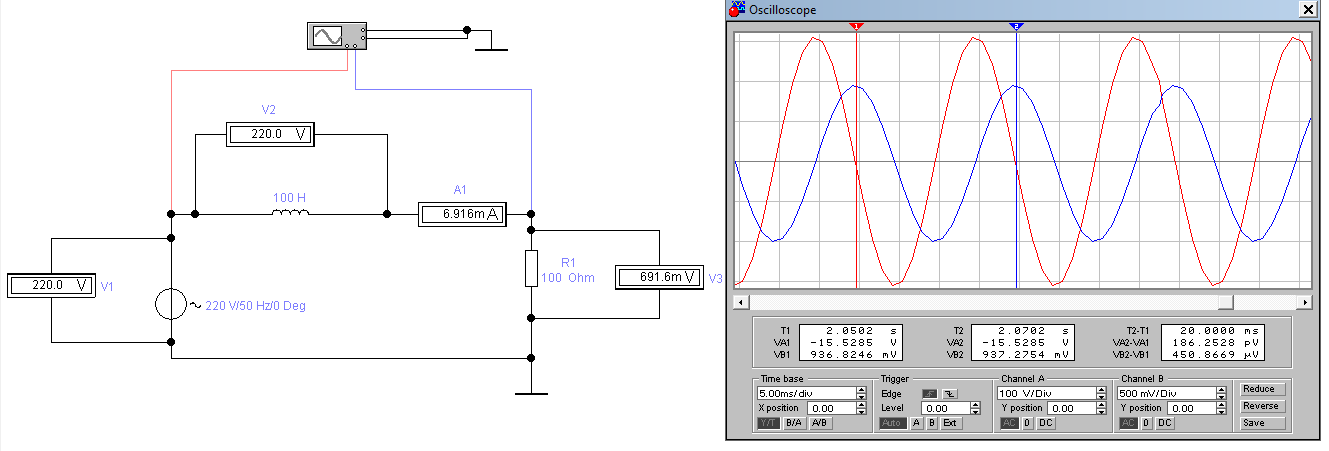 Рис. 2.2.1 Схема для измерения сдвига фаз между напряжением и током в RL цепи.
Рис. 2.2.1 Схема для измерения сдвига фаз между напряжением и током в RL цепи.
Применим описанные в пункте 1.2 действия для трёх различных параметров электрической цепи и полученные результаты вместе с показаниями измерительных приборов (амперметра и вольтметра) занесём в таблицу 2.2.1.
цепи с подключёнными к ней осциллографами для измерения временного сдвига представлена на рисунке 2.2.2.
| ∆T |

Рисунок 2.2.2. Цепь с параметрами E1= 220 В; f= 50Гц; L= 100Гн; R= 100 Ом
Для цепи с параметрами E1= 220 В; f= 50Гц; L= 100Гн; R= 100 Ом
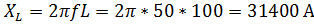
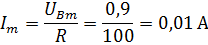
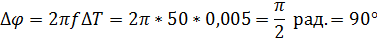

Для цепи с параметрами E1= 220 В; f= 100Гц; L= 50Гн; R= 1 кОм
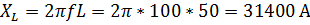
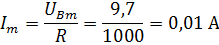


Для цепи с параметрами E1= 220 В; f= 50Гц; L= 100Гн; R= 20 Ом
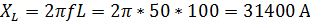
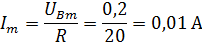
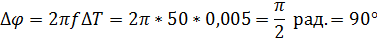

Таблица 2.2.1.
| A1 (А) | V1 (В) | XL (Ом) | UAm (В) | UBm (В) | TA (с) | TB (с) | ∆T (с) | Im (А) | ∆ 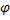 (град.) (град.)
| ||
| измерения | расчёт | ||||||||||
| E1= 220 В; f= 50Гц; L= 100Гн; R= 100 Ом | |||||||||||
| 0,0069 | 309,8 | 0,89 | 0,02 | 0,02 | 0,005 | 0,01 | 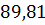
| ||||
| E1= 220 В; f= 100Гц; L= 50Гн; R= 1 кОм | |||||||||||
| 0,0069 | 309,8 | 9,7 | 0,01 | 0,01 | 0,0025 | 0,01 | 
| ||||
| E1= 220 В; f= 50Гц; L= 100Гн; R= 20 Ом | |||||||||||
| 0,0069 | 309,8 | 0,19 | 0,02 | 0,02 | 0,005 | 0,01 | 
| ||||
В ходе опыта было установлено, что угол сдвига фаз в RL цепи не зависит от ёмкости катушки, активного сопротивления резистора и частоты ЭДС источника. Измеренные значения угла сдвига фаз практически равны своему теоретическому значению.
3 Измерение параметров разветвлённой цепи переменного тока
| I3 |
| I2 |

| I1 |
| ветвь 1 |
| ветвь 2 |
| ветвь 3 |
Для двух различных параметров электрической цепи, представленных на рисунках 3.2-3.3, занесём показания измерительных приборов (амперметра и вольтметра) в таблицу 3.2.
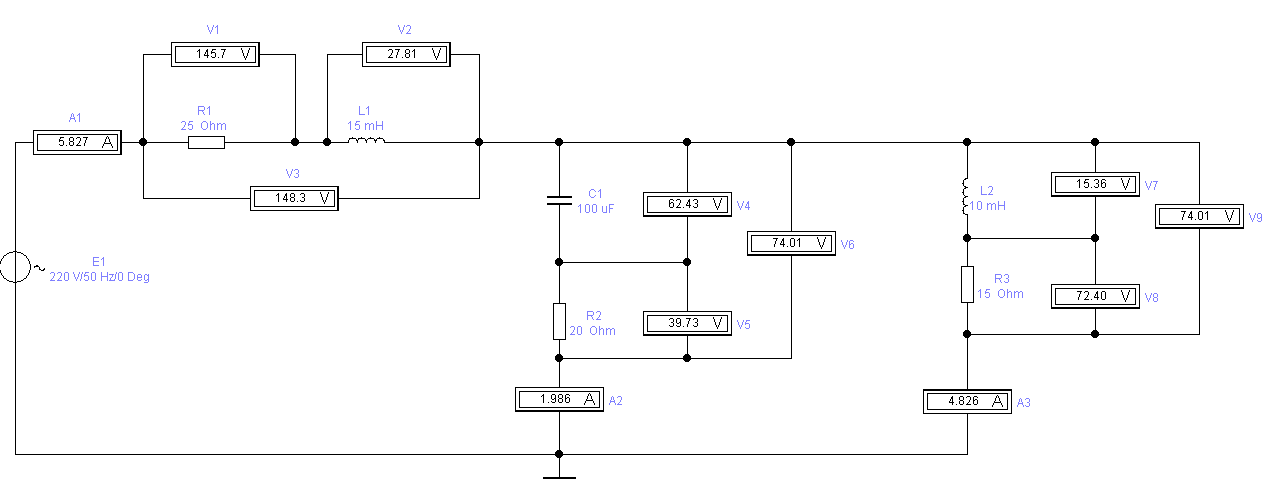
Рис. 3.2. Цепь с параметрами E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 25 Ом; R2= 20 Ом; R3= 15 Ом.

Рис. 3.3. Цепь с параметрами E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 500 Ом; R2= 120 Ом; R3= 1500 Ом.
Как видно из схемы суммарное напряжение каждой из ветвей не соответствует алгебраической сумме напряжений последовательно соединённых элементов соответствующей ветви. Это обусловлено тем, что в цепях переменного тока неприменимы в явном виде многие законы и правила по которым рассчитываются цепи постоянного тока. Для применения законов Ома и Кирхгофа необходимо представить напряжения и токи в комплексной форме. При этом ёмкостные и индуктивные элементы имеют реактивные характеристики, значит  , где
, где 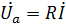 (активная составляющая напряжения),
(активная составляющая напряжения),  (реактивная составляющая напряжения),
(реактивная составляющая напряжения), 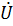 – общее напряжение ветви.
– общее напряжение ветви.
На рисунке 3.4 представлена комплексная плоскость напряжений.
| +j |
| +1 |

|

|

|
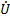
|

|
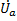
|

|
Рис. 3.4 Комплексная плоскость напряжений
Модуль вектора активной составляющей напряжения  совпадает по фазе с вектором тока
совпадает по фазе с вектором тока  . Модуль вектора реактивной составляющей напряжения
. Модуль вектора реактивной составляющей напряжения  сдвинут по фазе относительно тока на угол
сдвинут по фазе относительно тока на угол  . Индуктивное реактивное напряжение опережает по фазе ток на угол
. Индуктивное реактивное напряжение опережает по фазе ток на угол  (как показано на рисунке), а ёмкостное реактивное напряжение отстаёт от по фазе от тока на угол
(как показано на рисунке), а ёмкостное реактивное напряжение отстаёт от по фазе от тока на угол  . Из треугольника напряжений следует:
. Из треугольника напряжений следует:
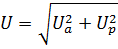
Тогда:
1) Для цепи E1= 220 В; f= 50Гц; L1= 15 мГн; L2= 10 мГн; С1=10мкФ; R1= 25 Ом; R2= 20 Ом; R3= 15 Ом.
1) 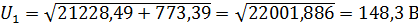
2) 
3) 
2) Для цепи E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 500 Ом; R2= 120 Ом; R3= 1500 Ом.
1) 
2) 
3) 
Результаты расчётов и показания приборов занесём в таблицу 3.1.
Таблица 3.1 Результаты расчётов и показаний приборов в разветвлённой цепи
 (В) (В)
| 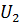 (В) (В)
|  (В) (В)
| |
| E1= 220 В; f= 50Гц; L1= 15 мГн; L2= 10 мГн; С1=10мкФ; R1= 25 Ом; R2= 20 Ом; R3= 15 Ом. | |||
| Результаты расчётов | 148,3 | 73,99 | 74,01 |
| Показания приборов | 148,3 | 74,01 | 74,01 |
| E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 500 Ом; R2= 120 Ом; R3= 1500 Ом. | |||
| Результаты расчётов | 180,1 | 40,3 | 40,3 |
| Показания приборов | 180,2 | 40,33 | 40,33 |
Таблица 3.2 Показания измерительных приборов в разветвлённой цепи.
| А1 (А) | А2 (А) | А3 (А) | V1 (В) | V2 (В) | V3 (В) | V4 (В) | V5 (В) | V6 (В) | V7 (В) | V8 (В) | V9 (В) |
| E1= 220 В; f= 50Гц; L1= 15 мГн; L2= 10 мГн; С1=10мкФ; R1= 25 Ом; R2= 20 Ом; R3= 15 Ом. | |||||||||||
| 5,8 | 1,98 | 4,8 | 145,7 | 27,8 | 148,3 | 62,43 | 39,73 | 15,3 | 72,4 | ||
| E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 500 Ом; R2= 120 Ом; R3= 1500 Ом. | |||||||||||
| 0,35 | 0,33 | 0,02 | 179,8 | 11,45 | 5,2 | 40,3 | 1,7 | 40,3 | 40,3 |
Рассчитаем активную, реактивную и полную мощность в ветвях электрической цепи по следующим формулам:
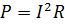 (активная мощность)
(активная мощность)
 (реактивная мощность)
(реактивная мощность)
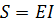 (полная мощность)
(полная мощность)
1) Для цепи E1= 220 В; f= 50Гц; L1= 15 мГн; L2= 10 мГн; С1=10мкФ; R1= 25 Ом; R2= 20 Ом; R3= 15 Ом.
Активные мощности
1)  ;
;
2)  ;
;
3) 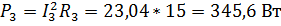 ;
;
Полная мощность
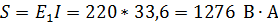
Реактивные мощности
1) 
2) 
3) 
Составим уравнение баланса мощностей:
Мощность, генерируемая источниками равна сумме мощностей потребляемых приёмниками.

Для данной цепи:
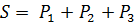

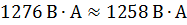
Условие баланса мощностей выполняется, значит, цепь рассчитана, верно
2) Для цепи E1= 220 В; f= 100Гц; L1= 50 мГн; L2= 100 мГн; С1=100 мкФ; R1= 500 Ом; R2= 120 Ом; R3= 1500 Ом.
Активные мощности
1) 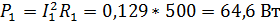 ;
;
2)  ;
;
3)  ;
;
Полная мощность
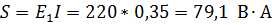
Реактивные мощности
1) 
2) 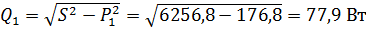
3) 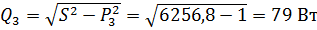
Составим уравнение баланса мощностей:
Мощность, генерируемая источниками равна сумме мощностей потребляемых приёмниками.

Для данной цепи:
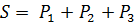
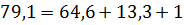

Условие баланса мощностей выполняется, значит, цепь рассчитана, верно.
Вывод
В результате работы были изучение фазовые соотношения и свойства элементов электрических цепей переменного тока и получены навыки измерения и расчёта их параметров в системе компьютерного моделирования.
В ходе работы было изучено явление переменного тока. Переменный ток – ток, меняющийся по величине и направленности с течением времени. Переменный ток, мгновенные значения и направления повторяются через равные промежутки времени (периоды) называется периодическим, а цепи в которых ток и напряжение (ЭДС) изменяются по гармоническому закону принято называть электрическими цепями переменного тока. Любые гармонические колебания характеризуются тремя основными параметрами: амплитудой, угловой частотой и начальной фазой. В лабораторной работе изучались фазы колебаний напряжения и тока, а именно – фазовый сдвиг (разность фаз, равная разности начальных фаз). По фазовому сдвигу можно судить о характере колебаний, а так же об опережении или отставании тока от напряжения и наоборот.
Для цепей переменного тока неприемлемо напрямую применять законы Ома и Кирхгофа. Для расчёта электрических цепей переменного тока необходимо выразить токи и напряжения в комплексном виде. Тогда, пользуясь правилами работы с комплексными числами, становиться возможным применение законов Ома и Кирхгофа для разрешения системы уравнений. Таким образом, находятся значения токов и напряжений в электрических цепях переменного тока.
Работу выполнил Благочиннов Е.Д. _____________
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 1829; Нарушение авторских прав?; Мы поможем в написании вашей работы!