
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 7 1 страница
|
|
|
|
1. Представление синусоидальных величин вращающимися векторами (рис.2.3).

Векторное изображение синусоидальных величин: а) – вращающийся вектор; б) – кривая изменения его проекции на ось Оа.
Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.
Любую синусоидально изменяющуюся во времени величину можно изображать вращающимся вектором, длина которого равна амплитуде, а угловая скорость вращения – угловой частоте этой синусоидальной величины. Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины y и отклоняемым от положительного направления оси ОХ в сторону, противоположную вращению часовой стрелки.
2. Представление синусоидальных величин с помощью комплексных чисел. Символический метод.
Символический метод или метод комплексных чисел соединяет в себе достоинства аналитического способа с наглядностью, присущей геометрической интерпретации.
Пользуясь понятием «комплексное число» и условным представлением напряжения или тока в виде вектора можно поместить вектор в комплексной плоскости (+j; +1), и выразить его в комплексной форме. Тогда вещественная (действительная) часть будет проекцией вектора на одно направление, а мнимая – на другое, перпендикулярное. (рис. 2.4)
Представление векторов в виде комплексных чисел позволяет заменить геометрические операции над векторами алгебраическими действиями над их комплексами и, таким образом, выполнить любую задачу аналитическим способом.

Представление вектора в комплексной плоскости: · - комплексное число, A m – комплексная амплитуда, А – комплексное действующее значение синусоидальной величины A = A m/√2=AeiΨ (A<Ψ).
Комплексное число А в общем случае состоит из вещественной А¢ и мнимой А² частей: А=А¢+jА²
Проекция на вещественную ось +1 соответствует вещественной части комплексного числа -А¢.
Проекция вектора на мнимую ось j (ось ординат) соответствует коэффициенту при мнимой единице j-А².
Мнимая единица j представляет собой поворотный множитель, умножение на который означает поворот вектора на 90о против часовой стрелки, т.е. поворот в положительном направлении.
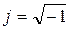 ;
;  ;
; 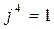
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число. 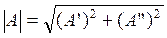
Аргумент комплексного числа определяется выражением 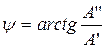
и показывает угол, на который повёрнут вектор по отношению к положительному направлению вещественной оси +1.
 Таким образом, любой вектор однозначно изображается комплексным числом, соответствующим концу этого вектора, т.е. точке.
Таким образом, любой вектор однозначно изображается комплексным числом, соответствующим концу этого вектора, т.е. точке.
Комплексный метод расчёта применим только к цепям с синусоидальными ЭДС, напряжениями и токами, т.к. только синусоидальные величины можно изобразить векторами.
Существуют 3 формы записи комплексного числа:
1)алгебраическая: A =A’+jA” или зачастую записывают так:

где  и
и 
- действительная и мнимая составляющие комплексного значения синусоидальной величины:

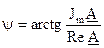
2) тригонометрическая: 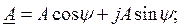
3)показательная: 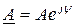
Переход от показательной формы к тригонометрической выполняется при помощи формулы Эйлера:

Комплекс может быть выражен также в показательной форме:
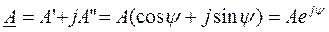
Здесь 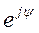 представляет собой так называемый поворотный множитель, показывающий, вектор длиной А повёрнут относительно положительного направления вещественной оси +1 на угол y.
представляет собой так называемый поворотный множитель, показывающий, вектор длиной А повёрнут относительно положительного направления вещественной оси +1 на угол y.
Сложение и вычитание комплексных чисел производится только в алгебраической форме.
Умножение и деление комплексных чисел можно производить в алгебраической форме, однако это удобнее произвести в показательной форме.
Вопрос 8
Индуктивная катушка как элемент схемы замещения реальной цепи синусоидального тока дает возможность учитывать при расчете явление самоиндукции и явление накопления энергии в ее магнитном поле. Пусть в цепь переменного тока (рис 2.7 а) включена катушка с бесконечно малым сопротивлением провода 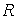 = 0. Непрерывное во времени изменение тока вызывает появление в витках катушки ЭДС самоиндукции. В соответствии с правилом Ленца эта ЭДС противодействует изменению тока.
= 0. Непрерывное во времени изменение тока вызывает появление в витках катушки ЭДС самоиндукции. В соответствии с правилом Ленца эта ЭДС противодействует изменению тока.
Допустим, ток через катушку изменяется по закону
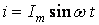 . (2.13)
. (2.13)
В этом случае ЭДС самоиндукции
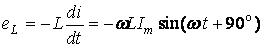 . (2.14)
. (2.14)
Поэтому напряжение на катушке
 . (2.15)
. (2.15)
Сравнивая формулы (2.13) и (2.15), можно сделать вывод о том, что напряжение на катушке опережает ток на угол  или ток отстает от напряжения по фазе на угол
или ток отстает от напряжения по фазе на угол  (рис 2.7 б). Угол сдвига фаз в этом случае положительный (рис. 2.7 в)
(рис 2.7 б). Угол сдвига фаз в этом случае положительный (рис. 2.7 в)  . Параметр цепи
. Параметр цепи  – индуктивное сопротивление, имеющее размерность Ом. Оно зависит от частоты и представляет собой величину, с помощью которой учитывается явление самоиндукции.
– индуктивное сопротивление, имеющее размерность Ом. Оно зависит от частоты и представляет собой величину, с помощью которой учитывается явление самоиндукции.
Из анализа (2.14) видно, что амплитуды напряжения и тока связаны законом Ома:
 .
.
Аналогично для действующих значений
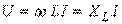 .
.
Мгновенная мощность цепи с катушкой

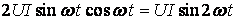 . (2.16)
. (2.16)
Из графика (рис 2.7 г), построенного по уравнению (2.16), видно, что за первую четверть периода, когда  > 0 и
> 0 и  > 0, площадь, ограниченная кривой
> 0, площадь, ограниченная кривой  и осью абсцисс, пропорциональна энергии, потребляемой катушкой на создание магнитного поля. Во вторую четверть периода (ток убывает от максимума до нуля) энергия магнитного поля катушки передается источнику питания. При этом мгновенная мощность отрицательна, а процесс повторяется. Таким образом, происходит колебание энергии между источником и катушкой, причем активная мощность, поступающая в катушку, равна нулю. Амплитуду колебания мгновенной мощности в цепи с катушкой называют реактивной (индуктивной) мощностью
и осью абсцисс, пропорциональна энергии, потребляемой катушкой на создание магнитного поля. Во вторую четверть периода (ток убывает от максимума до нуля) энергия магнитного поля катушки передается источнику питания. При этом мгновенная мощность отрицательна, а процесс повторяется. Таким образом, происходит колебание энергии между источником и катушкой, причем активная мощность, поступающая в катушку, равна нулю. Амплитуду колебания мгновенной мощности в цепи с катушкой называют реактивной (индуктивной) мощностью
 .
.
Реактивную мощность в отличие от активной мощности измеряют в вар (вольт-ампер реактивный).
Зависимость ЭДС генератора от тока возбуждения называется характеристикой холостого хода E = Uхх = f (Iв).
Характеристику холостого хода получают при разомкнутой внешней цепи (Iя) и при постоянной частоте вращения (n2 = const)
Характеристика холостого хода генератора показана на рис. 11.8.
Из-за остаточного магнитного потока ЭДС генератора не равна нулю при токе возбуждения, равном нулю.
При увеличении тока возбуждения ЭДС генератора сначала возрастает пропорционально.
Соответствующая часть характеристики холостого хода будет прямолинейна. Но при дальнейшем увеличении тока возбуждения происходит магнитное насыщение машины, отчего кривая будет иметь изгиб. При последующем возрастании тока возбуждения ЭДС генератора почти не меняется. Если уменьшать ток возбуждения, кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса.
Зависимость напряжения на внешних зажимах машины от величины тока нагрузки
U = f (I) при токе возбуждения Iв = const называют внешней характеристикой генератора.
Вопрос 9
Включение конденсатора в цепь переменного тока не вызывает разрыва цепи, так как ток в цепи все время поддерживается за счет заряда и разряда конденсатора. Пусть напряжение (рис. 2.8 а)
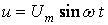 ,тогда
,тогда


 (2.17)
(2.17)
Формула (2.17) показывает, что ток опережает приложенное напряжение на угол  . Нулевым значениям тока соответствуют максимальные значения напряжения. Физически это объясняется тем, что при достижении электрическим зарядом и соответственно напряжением максимального значения ток становится равным нулю.
. Нулевым значениям тока соответствуют максимальные значения напряжения. Физически это объясняется тем, что при достижении электрическим зарядом и соответственно напряжением максимального значения ток становится равным нулю.
Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т.е.
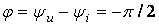 .
.
Таким образом, в отличие от цепи с катушкой, где 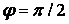 , угол сдвига фаз в цепи с конденсатором отрицателен.
, угол сдвига фаз в цепи с конденсатором отрицателен.
Из (2.17) видно, что амплитуды тока и напряжения связаны законом Ома
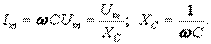 , где
, где 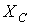 – емкостное сопротивление, имеющее размерность Ом.
– емкостное сопротивление, имеющее размерность Ом.
Мгновенная мощность, поступающая в конденсатор
 ,
,
колеблется синусоидально с угловой частотой 2  , имея амплитуду, равную
, имея амплитуду, равную 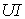 (рис. 2.8 г). Поступая от источника, энергия временно запасается в электрическом поле конденсатора, затем возвращается источнику при исчезновении электрического поля. Таким образом, здесь, как и в цепи с катушкой, происходит колебание энергии между источником и конденсатором, причем активная мощность
(рис. 2.8 г). Поступая от источника, энергия временно запасается в электрическом поле конденсатора, затем возвращается источнику при исчезновении электрического поля. Таким образом, здесь, как и в цепи с катушкой, происходит колебание энергии между источником и конденсатором, причем активная мощность  = 0. Амплитуду колебания мощности в цепи с конденсатором называют реактивной (емкостной) мощностью
= 0. Амплитуду колебания мощности в цепи с конденсатором называют реактивной (емкостной) мощностью
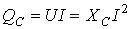 .
.
Зависимость ЭДС генератора от тока возбуждения называется характеристикой холостого хода E = Uхх = f (Iв).
Характеристику холостого хода получают при разомкнутой внешней цепи (Iя) и при постоянной частоте вращения (n2 = const)
Характеристика холостого хода генератора показана на рис. 11.8.
Из-за остаточного магнитного потока ЭДС генератора не равна нулю при токе возбуждения, равном нулю.
При увеличении тока возбуждения ЭДС генератора сначала возрастает пропорционально.
Соответствующая часть характеристики холостого хода будет прямолинейна. Но при дальнейшем увеличении тока возбуждения происходит магнитное насыщение машины, отчего кривая будет иметь изгиб. При последующем возрастании тока возбуждения ЭДС генератора почти не меняется. Если уменьшать ток возбуждения, кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса.
Зависимость напряжения на внешних зажимах машины от величины тока нагрузки
U = f (I) при токе возбуждения Iв = const называют внешней характеристикой генератора.
Вопрос 10
Множитель в уравнении (3.30) представляет собой комплекс, имеет размерность сопротивления и обозначается через Z. Его называют комплексным сопротивлением:
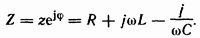
Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.
Уравнение (3.30) можно записать так: Разделим обе его части на и перейдем от комплексных амплитуд к комплексам действующих значений и Е:

Уравнение (3.30) представляет собой закон Ома для цепи синусоидального тока.
В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть
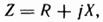
где R — активное сопротивление; X — реактивное сопротивление. Для схемы (см. рис. 3.9) реактивное сопротивление 
Активное сопротивление (резистивный элемент – рис. 2.7).
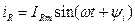
 для мгновенных значений напряжения и тока справедливо соотношение: где
для мгновенных значений напряжения и тока справедливо соотношение: где 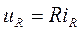
или 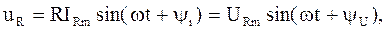
где амплитуды тока и напряжения связаны выражением 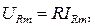 (2.7)
(2.7)
а их начальные фазы одинаковы: 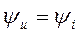 (2.8)
(2.8)
Ток и напряжение в активном сопротивлении изменяются синфазно, т.е. совпадают по фазе. (см. рис. 2.7.а).
Разделив (2.7) на 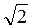 получим соотношения для действующих значений U и I или закон Ома в комплексном виде для активного сопротивления (резистивного элемента R):
получим соотношения для действующих значений U и I или закон Ома в комплексном виде для активного сопротивления (резистивного элемента R): 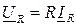 (2.9) Действующие значения синусоидальных напряжений и токов связаны между собой законом Ома так же как постоянные напряжения и ток.
(2.9) Действующие значения синусоидальных напряжений и токов связаны между собой законом Ома так же как постоянные напряжения и ток.
Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению: Y=I/U=1/Z=1/(zejj)=ye‑jj=yÐ‑j, (6.31а)
где y=1/z — величина, обратная полному сопротивлению, называется полной проводимостью.
Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде
Y= ye‑jj=ycosj‑jysinj=g‑jb, (6.31б)
где g=ycosj — действительная часть комплексной проводимости, называется активной проводимостью; b=ysinj — значение мнимой части комплексной проводимости, называется реактивной проводимостью;
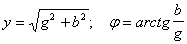 .(6.32)
.(6.32)
Из (6.30) и (6.29) следует, что для схемы, представленной на рис. 6.12, комплексная проводимость
Y=1/r‑j[1/(wL)‑wC]=g‑j(bL‑bC), где g=1/r; bL=1/(wL)=1/xL; bC=wC=1/xС
и называются соответственно активной, индуктивной и емкостной проводимостями.
Реактивная проводимость
b=bL‑bC. (6.33)
Вопрос 11
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
Первый: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:  , (2.8) где n – число ветвей, сходящихся в узле.
, (2.8) где n – число ветвей, сходящихся в узле.
Второй: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
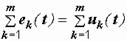 (2.9) где m – число ветвей, образующих контур.
(2.9) где m – число ветвей, образующих контур.
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
| ЗаконыКирхгофа в векторной форме: | ЗаконыКирхгофа в символической форме: |
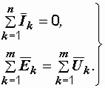 (2.10) (2.10)
|  (2.11) (2.11)
|
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (2.8) и (2.9); применение метода векторных диаграмм, основанного на уравнениях (2.10), использование в расчетах комплексных чисел и уравнений (2.11), являющихся основой символического метода.
Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 2.14).
| Токи первых двух ветвей известны: i1 = 8sin(w t+30°) А, i2 = 6sin(w t+120°) А. Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы. | 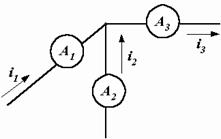 Рис. 2.14. Узел электрической цепи
Рис. 2.14. Узел электрической цепи
|
Решение 1. Непосредственное сложение синусоид:
i3 = i1+i2 = 8sin(w t+30°)+6sin(w t+120°) = I3msin(w t+y 3).
Сумма двух синусоид одинаковой частоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:

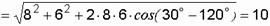 A,
A,
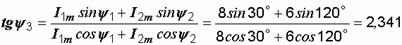 ,
,
откуда y 3 = 66,87°. Итак, i3 = 10 sin (w t+66,87°)
2. Применение метода векторных диаграмм.
В соответствии с первым законом Кирхгофа в векторной форме для цепи на рис. 2.14 имеем  . В прямоугольной системе координат строим векторы
. В прямоугольной системе координат строим векторы  и
и 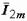 и находим вектор
и находим вектор 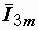 , равный их сумме (рис. 2.15).
, равный их сумме (рис. 2.15).
Так как треугольник oab прямоугольный, а сторона ab равна длине вектора I2m, то 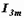 = =  А.
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси: А.
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной оси: 
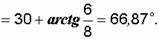
| 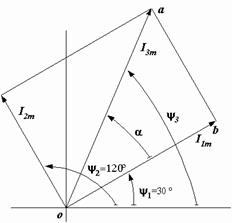 Рис. 2.15. Векторная диаграмма токов
Рис. 2.15. Векторная диаграмма токов
|
3. Решение символическим методом.
Записываем комплексные амплитуды первого и второго токов:
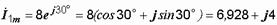 A,
A,
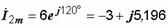 A
A
По первому закону Кирхгофа в символической форме
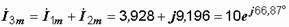 А.
А.
Модуль последнего комплексного числа равен амплитуде третьего тока, а аргумент – начальной фазе. Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, поэтому
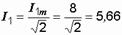 A,
A, 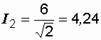 A,
A,  A.
A.
Обращаем внимание на то, что 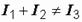 . Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
. Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.
Метод векторных диаграмм удобен при решении относительно несложных задач.
В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.
Вопрос 20
Трансформатором называют статическое устройство, имеющее две (или более) индуктивно связанных обмоток и предназначенное для преобразования посредством электромагнитной индукции одной или нескольких систем переменного тока в одну или несколько других систем переменного тока.
1. В работе трансформатора важную роль играет то положение, что при изменении нагрузки трансформатора в широком диапазоне магнитный поток может считаться практически неизменным. Напряжение на зажимах первичной обмотки U 1 и наводимая в ней э.д.с. E 1 связаны комплексным уравнением U 1=- E 1+ I1Z1. Иначе говоря, напряжение U 1 уравновешивается электродвижущей силой E 1 и падением напряжения в первичной обмотке, которое очень невелико. Поэтому E 1 лишь незначительно отличается от U 1, составляя при нормальной нагрузке (0,95÷0,97) U1. Увеличение тока (даже в два раза) может вызвать уменьшение э.д.с. E 1 всего до (0,93÷0,95) U 1. Таким образом, изменение э.д.с. E 1 настолько незначительно, что практически эта э.д.с. может считаться неизменной. Но э.д.с. E 1 пропорциональна амплитудному значению магнитного потока: E1 =4,44 f w Фm. Отсюда и вытекает сформулированное выше положение о неизменности магнитного потока.
Основываясь на этом положении, можно объяснить, почему при изменении нагрузки трансформатора, а следовательно, и тока во вторичной обмотке I 2 одновременно изменяется и ток в первичной обмотке I 1. Магнитный поток Ф создается намагничивающей силой, которая выражается как сумма намагничивающих сил первичной и вторичной обмоток: F = I 1w1+ I 2w2. Постоянству магнитного потока соответствует постоянство создающей его магнитной силы. Всякое изменение тока I 2 принуждает изменяться поток I 1 настолько, чтобы общая намагничивающая сила обмоток оставалась неизменной. Положение о неизменности магнитного потока относится не только к трансформаторам, но также и к машинам переменного тока - асинхронным и синхронным.
2. Для лучшего понимания и усвоения принципа работы нагруженного трансформатора целесообразно использовать так называемую условно-логическую схему, показанную на рис. Представленная схема читается следующим образом.
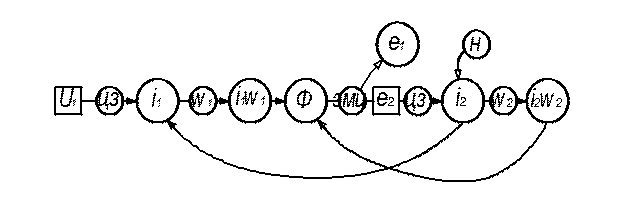
Рисунок 5.АВ
К цепи первичной обмотки трансформатора подается переменное напряжение u1, и так как цепь замкнута (ЦЗ), по первичной обмотке протекает ток i1; первичная обмотка имеет w1 витков, поэтому она создает м.д.с. i1 w 1; м.д.с. является возбудителем магнитного потока Ф; магнитный поток переменный, поэтому в соответствии с законом электромагнитной индукции (ЭМИ) в обеих обмотках наводятся e1 и e2. Полученная э.д.с. e2 является преобразованной величиной напряжения u1. Если трансформатор работает под нагрузкой, то цепь вторичной обмотки замкнута (ЦЗ) и поэтому в ней протекает ток i2 (величина которого зависит от нагрузки Н). Эта обмотка имеет w2 витков и в результате м.д.с. i2 w 2 действует на магнитный поток Ф. Это воздействие уменьшает Ф, но одновременно увеличивается ток i1 (под влиянием нагрузки или в связи с увеличением нагрузки), в результате чего увеличивается i1 w 1.
Следует иметь в виду, что схема поясняет принцип работы, а не все дополнительные явления, сопутствующие принципу работы. Так, в данном случае опущен вопрос о возникновении э.д.с. рассеяния. При объяснении схемы следует подчеркнуть, что Ф, т.е. результирующий магнитный поток, является главным, основным. Наряду с этим в схеме хорошо показаны обратные связи.
3. При построении векторных диаграмм трансформатора следует иметь в виду, что лишь первый шаг является произвольным. Пусть, например, из произвольно выбранной точки в произвольном направлении проведен вектор тока I 1; остальные построения будут уже обусловлены, с одной стороны, заданными значениями угла φ2 и напряжением U 2, с другой – уравнениями напряжений и токов для вторичной и первичной обмоток трансформатора.
В рассматриваемом случае после проведения вектора I 2 под заданным углом φ2 к нему строится вектор U2. Далее к вектору напряжения U 2 прибавляются I 2r2 и j I ’2x2 получаетсякак результирующий вектор E ’2. В дальнейшем построении также нет никаких произвольных элементов. Под углом π/2 в сторону опережения проводится вектор магнитного потока Фm, а затем вектор тока холостого хода I 0. К вектору – E 1 прибавляются векторы I 1r1 и j I 1x1 и в результате строится вектор U 1.
4. При рассмотрении изменения вторичного напряжения следует обратить внимание на активную нагрузку. При такой нагрузке φ2=0 и поэтому формула процентного изменения напряжения приводится к виду ∆U %=βuк.а. Отсюда следует, что при нормальной нагрузке величиной ∆U можно пренебречь, так как uк.а=1÷2 %.
5. В теории трансформаторов пользуются схемой замещения. Возможность представить трансформатор его схемой замещения вытекает из теории четырехполюсника, поскольку трансформатор может рассматриваться как четырехполюсник. Подобная же схема замещения используется и в теории асинхронных машин вследствие существования некоторой аналогии между процессами, происходящими в асинхронной машине и трансформаторе. Использование схемы замещения означает, что вместо реального объекта – электрической машины – рассматривается его схема. Соотношение в реальном объекте (электрической машине) и аналоге (схеме замещения) описываются уравнениями одинакового вида. В то же время схема замещения значительно проще и нагляднее, нежели сама электрическая машина.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 628; Нарушение авторских прав?; Мы поможем в написании вашей работы!