
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 7 2 страница
|
|
|
|
6. В трехфазных трансформаторах алгебраическая сумма мгновенных значений синусоидальных магнитных потоков в сердечнике равна нулю, поэтому необходимость в «нейтральном» стержне отпадает и трехфазный трансформатор выполняется в виде трехстержневого.
7. Теория однофазного трансформатора полностью распространяется на автотрансформаторы и измерительные трансформаторы. Поэтому при изучении последних следует обратить внимание на область применения, их особенности и возникающие дополнительные погрешности (в измерительных трансформаторах)
Назначение трансформаторов.
Трансформаторы предназначены для:
а) Изменения напряжения вырабатывающих генераторов с 10-20 кВ до 35, 110, 220, 330, 500, 750 кВ с целью повышения КПД ЛЭП и уменьшения затрат на цветной металл.
б) Понижения напряжения на местах потребления электроэнергии до такого уровня, который является номинальным для электроприёмников: 220, 380 В и т.д.
в) Применения в установках электросварки, в радио- и телеустановках, в системах автоматического управления, связи и т.п.
Наибольшее распространение получили следующие типы трансформаторов:
1) силовые – для передачи и распределения электроэнергии;
2) автотрансформаторы – для преобразования напряжения в небольших пределах, для пуска двигателей переменного тока и т.п.;
3) измерительные трансформаторы – для включения в схемы измерительных приборов;
4) трансформаторы специального назначения – сварочные, печные, испытательные, импульсные, пиковые, высокочастотные, для преобразования частоты, для медицинских и радиотехнических целей.
Таким образом, область применения трансформаторов чрезвычайно широка, соответственно велико и число конструктивных форм трансформаторов. Но во всех случаях процесс преобразования энергии в трансформаторах и приемы изучения происходящих в них явлений по существу одни и те же. Поэтому в дальнейшем рабочие процессы рассматриваются в основном трансформаторам– в одно и трехфазном двухобмоточном силовом трансформаторе.
Вопрос 23
Способ связывания фаз звезды и треугольника ( -
-  ). Характерной особенностью такого соединения является равенство фазных напряжений приемника соответствующим линейным напряжениям генератора, т. е.
). Характерной особенностью такого соединения является равенство фазных напряжений приемника соответствующим линейным напряжениям генератора, т. е. 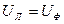
Первичные и вторичные обмотки трехфазных трансформаторов могут соединяться по схемам звезды или треугольника.
Обмотку высшего напряжения трансформатора с экономической точки зрения выгоднее соединять звездой, т.к. для получения заданного линейного напряжения 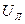 требуется фазное напряжение U
требуется фазное напряжение U  , а, следовательно, требуется меньшее число витков обмотки и облегченная ее изоляция. (Т.к. число витков обмотки трансформатора прямо пропорционально напряжению, то при соединении звездой для каждой из обмоток необходимо меньшее число витков, но с большим сечением и с изоляцией, рассчитанной лишь на фазное напряжение).Соединение обмоток треугольником конструктивно оправданно при больших токах.
, а, следовательно, требуется меньшее число витков обмотки и облегченная ее изоляция. (Т.к. число витков обмотки трансформатора прямо пропорционально напряжению, то при соединении звездой для каждой из обмоток необходимо меньшее число витков, но с большим сечением и с изоляцией, рассчитанной лишь на фазное напряжение).Соединение обмоток треугольником конструктивно оправданно при больших токах.
По этой причине соединение звезда/треугольник ( /
/ 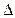 ) можно считать наиболее распространенным для трансформаторов большой мощности в тех случаях, когда на стороне низшего напряжения не нужен нейтральный провод.
) можно считать наиболее распространенным для трансформаторов большой мощности в тех случаях, когда на стороне низшего напряжения не нужен нейтральный провод.
При использовании трехфазных трансформаторов в сложных системах с большим числом трансформаций и при наличии параллельных ветвей с трансформаторами всегда необходимо знать сдвиг фаз между первичным и вторичным линейным напряжениями. Этот сдвиг характеризуется группой соединения обмоток.
Группа соединения в общем случае зависит от схемы соединения, направления намотки и выбора начала и конца обмоток.
У трансформаторов нормального исполнения направление намотки и обозначение выводов таково, что фазные ЭДС первичной и вторичной обмоток совпадают по фазе. Тогда группа соединения обмоток зависит только от схем их соединения.
Группа соединения обмоток трехфазного трансформатора определяется цифрой часового циферблата, на которую “указывает” вектор линейной вторичной ЭДС при условии, что вектор линейной первичной ЭДС “направлен на нуль часов”.
Примеры групп соединения обмоток:
1.Соединение  /
/  . (рис. 5.25) – нулевая группа.
. (рис. 5.25) – нулевая группа.
Сначала строят диаграмму фазных ЭДС (система симметрична – рис. 5.25б). Из векторных диаграмм видно, что при совпадении по фазе фазных ЭДС линейные ЭДС первичной и вторичной обмоток совпадают по фазе.
Таким образом, если повернуть на угол 300 по часовой стрелке вектор первичной линейной ЭДС Е АВ и направить его на цифру 0 (или 12) часового циферблата, то вектор вторичной линейной ЭДС Е ав после его поворота на 300 по часовой стрелке будет направлен также на 0.
При соединении первичной и вторичной обмоток треугольником (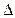 ) Е л= Е ф; следовательно, группа соединения обмоток будет также нулевой.
) Е л= Е ф; следовательно, группа соединения обмоток будет также нулевой.
Итак, группа соединения 0 получается при одинаковой схеме соединения первичной и вторичной обмоток.Эта группа соединения обозначается:  /
/  - 0,
- 0, 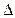 /
/ 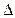 - 0.
- 0.
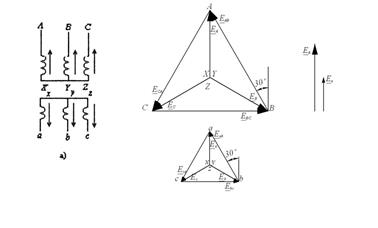 Рис.5.25 Нулевая группа соединения обмоток трехфазного трансформатора: а – схема трансформатора, б – векторные диаграммы первичной и вторичной обмоток.
Рис.5.25 Нулевая группа соединения обмоток трехфазного трансформатора: а – схема трансформатора, б – векторные диаграммы первичной и вторичной обмоток.
2.Соединение  /
/ 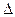 (рис. 5.26) – группа соединения 11.
(рис. 5.26) – группа соединения 11.
Векторная диаграмма ЭДС первичной обмотки (рис.5.26б) остается той же, что и на рис. 5.25б.
На векторной диаграмме ЭДС вторичной обмотки, соединенной D, фазная ЭДС Е ах= Е а совпадает по фазе с фазной ЭДС Е А , которая выбирается в качестве базовой (реперной). Поэтому вектор Е ах проводят параллельно вектору Е А.. ЭДС Е ах направлена из точки x в точку а (рис.5.26 а), соответственно обозначены начало и конец вектора Е ах (на рис5.26 б). При соединении D объединяют в одну точку начала и концы разных фаз: а и у, в и с, с и х. Потенциалы этих точек соответственно равны, и на векторной диаграмме конец вектора Е ах обозначен двумя буквами «а» и «у». Вектор ЭДС Е ву проводится из точки «у» параллельно вектору ЭДС Е в. Аналогично проводится вектор ЭДС Е сz. Определяя группу соединения по вектору первичной линейной ЭДС Е АВ, необходимо иметь вектор линейной ЭДС Е ав . Из векторной диаграммы для первичной обмотки видно, что вектор линейной ЭДС всегда направлен из точки, обозначающей второй индекс (В), в точку, обозначающую первый индекс (А). Следовательно, ЭДС Е ав направлена из точки в в точку а. На векторной диаграмме (рис.5.26б) построены линейные ЭДС вторичной обмотки: Е ав, Е вс, Е са.

Рис.5.26. Группа соединения обмоток трансформатора 11: а) схема трансформатора, б) векторные диаграммы обмоток трансформатора.
После поворота вектора ЭДС Е АВ на 300 по часовой стрелке совмещаем его с цифрой 0 на часовом циферблате. Вектор вторичной ЭДС Е ав после поворота также на 300 по часовой стрелке будет направлен на цифру 11, т.к. угол между векторами Е АВ и Е ав составляет 300.
Таким образом, при соединении  /
/ 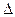 получили группу соединения 11(
получили группу соединения 11( /
/ 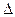 -11).
-11).
Согласно ГОСТ 1167-65 приняты и выпускаются трансформаторы со схемами и группами соединения 0 и 11.
Вопрос 22
Несвязанные цепи (рис.3.5.) не получили применения вследствие их неэкономичности, вызванной большим числом проводов, соединяющих источники питания и приемники (n=6). 
Более совершенными и экономичными являются связанные цепи, у которых концы фаз X,Y,Z соединяют в одну общую точку.
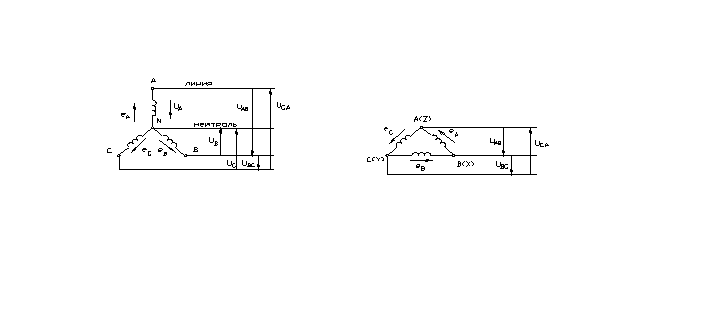
Схемы соединения фаз источника: а) звездой; б) треугольником.
На практике фазы трехфазных генераторов предпочитают соединять звездой ( ). Точки N и n называют нейтральными, а провод, соединяющий их, называют нейтральным.
). Точки N и n называют нейтральными, а провод, соединяющий их, называют нейтральным.
Напряжения между началом и концом фазы называют фазными  :
:  .
.
Напряжения между линейными проводами называют линейными  :
:  .
.
Пренебрегая внутренним сопротивлением генератора, можно считать фазные напряжения  равными фазным Э.Д.С. (
равными фазным Э.Д.С. (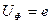 ).
).
 За условные положительные направления фазных напряжений принимают направление от начала (от точек A, B, C) к концу фаз обмоток (точка N), а линейных напряжений – от начала одной фазы к началу другой.
За условные положительные направления фазных напряжений принимают направление от начала (от точек A, B, C) к концу фаз обмоток (точка N), а линейных напряжений – от начала одной фазы к началу другой.
В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений (рис.3.6.а), можно записать (согласно II закону Кирхгофа) уравнения и построить по ним векторную диаграмму:

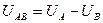 ;
; 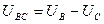 ;
;  .
.
Комплексные значения линейных напряжений:

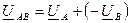 ;
; 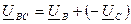 ;
; 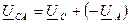 . (3.8.)
. (3.8.)
Это уравнение позволяет определить линейные напряжения по известным фазным напряжениям.
 Таким образом, действующее значение линейных напряжений равно векторной разностсоответствующих фазных напряжений.
Таким образом, действующее значение линейных напряжений равно векторной разностсоответствующих фазных напряжений.
Топографическая (потенциальная) диаграмма фазных и линейных напряжений при соединении фаз “звездой”.
Напряжение между отдельными точками трехфазной цепи целесообразно определять графически – путем построения так называемой топографической (потенциальной) диаграммы.
Топографическая диаграмма – это векторная диаграмма, построенная так, чтобы каждой точке цепи соответствовала определенная точка на диаграмме и чтобы вектор, проведенный в эту точку из начала координат, выражал по величине и фазе потенциал соответствующей точки цепи. Отрезок, соединяющий любые две точки на этой диаграмме, определяет напряжение между соответствующими точками цепи.
При построении топографической диаграммы для трехфазной цепи удобно принять за точку с нулевым потенциалом нулевую, или нейтральную точку генератора N. Этой точке генератора соответствует начало координат топографической диаграммы.
Для нахождения вектора линейного напряжения  (рис.3.7.), как следует из (3.8.) необходимо к вектору напряжения
(рис.3.7.), как следует из (3.8.) необходимо к вектору напряжения 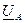 прибавить вектор напряжения
прибавить вектор напряжения 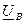 с противоположным знаком. После переноса вектора
с противоположным знаком. После переноса вектора  параллельно самому себе он соединит точки A и B на топографической диаграмме фазных напряжений. Аналогично строят векторы линейных напряжений
параллельно самому себе он соединит точки A и B на топографической диаграмме фазных напряжений. Аналогично строят векторы линейных напряжений 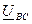 и
и  .
.
 Из диаграммы (рис.3.7.) видно, что для симметричной системы напряжений линейные напряжения представляют тремя векторами, сдвинутыми по фазе друг относительно друга на угол
Из диаграммы (рис.3.7.) видно, что для симметричной системы напряжений линейные напряжения представляют тремя векторами, сдвинутыми по фазе друг относительно друга на угол  (
(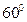 ), кроме того, векторы линейных напряжений
), кроме того, векторы линейных напряжений  опереют по фазе соответственно векторы фазных напряжений
опереют по фазе соответственно векторы фазных напряжений  на угол
на угол 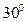 .
.
Величина каждого линейного напряжения в  раз больше величины вектора фазного напряжения:
раз больше величины вектора фазного напряжения: 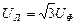 (
( )
)
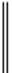 Важное свойство системы линейных напряжений:“Независимо от характера нагрузки сумма их мгновенных значений всегда равна нулю”, т.е.
Важное свойство системы линейных напряжений:“Независимо от характера нагрузки сумма их мгновенных значений всегда равна нулю”, т.е. 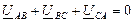 (3.8.а)
(3.8.а)
При соединении фаз источника треугольником линейные напряжения равны фазным:
 , (
, ( ) т.к. обмотка генератора, линейный провод и приемник, принадлежащие одной фазе, соединяются последовательно.
) т.к. обмотка генератора, линейный провод и приемник, принадлежащие одной фазе, соединяются последовательно.
Вопрос 24
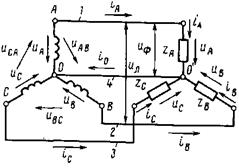
При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206). Приемники электрической энергии объединяют в три группы ZA, ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным. Напряжения uА, uв и uс между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA, ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках. Фазными токами iA, iB, ic называют токи, протекающие по обмоткам источника или фазам нагрузки ZA, ZB и Zc. Напряжения uAB, uBC, uCA между линейными проводами и токи, проходящие по этим проводам, называют линейными.
Примем условно за положительное направление токов iA, iB и ic в фазах источника — от конца соответствующей фазы к ее началу,
 206
206
в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику. Будем считать положительными напряжения uА, uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ, uBC, uСА — если они направлены от предыдущей фазы к последующей.
Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. Iл = Iф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений. Мгновенные значения напряжений согласно второму закону Кирхгофа:
 Вопрос 25
Вопрос 25
Симметричными называют приемники, комплексы сопротивлений фаз которых равны между собой: 
Если это условие не выполняется, то приемники называются несимметричными, при этом нагрузка может быть равномерной, если  или однородной, если
или однородной, если 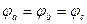 .
.
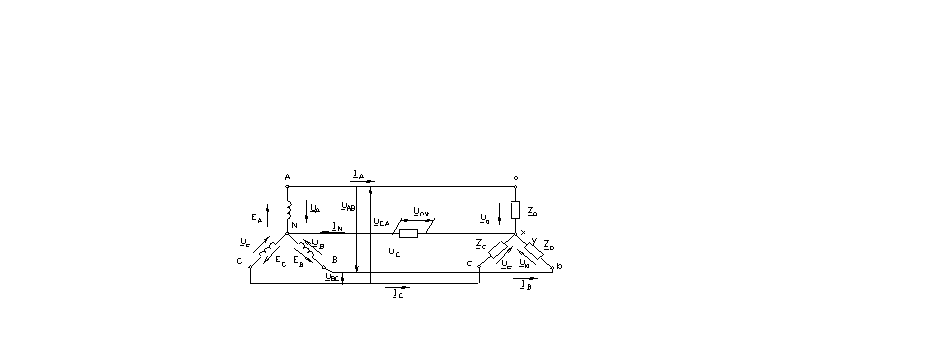
Рис. 3.8. Схема четырехпроводной трехфазной цепи.
Исходя из схемы рис. 3.8. и пренебрегая сопротивлениями линейных и нейтрального проводов, можно утверждать, что фазные напряжения приемника будут равны фазным напряжениям источника: 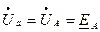 ;
; 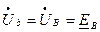 ;
;  .
.
Тогда токи в каждой фазе симметричной нагрузки (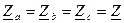 ):
):

 (3.9.)
(3.9.)
А ток в нейтральном проводе: 
При соединении фаз приемника  фазные и линейные токи равны между собой:
фазные и линейные токи равны между собой: 
При симметричной нагрузке токи в фазах равны по величине и сдвинуты по фазе на один и тот же угол относительно соответствующих фазных напряжений (рис. 3.9).
При симметричной нагрузке ток в нейтральном проводе отсутствует ( ) и необходимость в этом проводе отпадает. Четырехпроводная цепь без нейтрального провода становится трехпроводной.
) и необходимость в этом проводе отпадает. Четырехпроводная цепь без нейтрального провода становится трехпроводной.
Рассмотрим теперь вопрос, каковы будут линейные напряжения (рис.3.8.).Линейное напряжение, например, между фазами А и В может быть записано так (см. формулу 3.8): 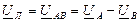 Используя оператор “ a ”, это выражение будет представлено таким образом:
Используя оператор “ a ”, это выражение будет представлено таким образом: 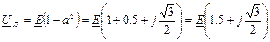 .
.
Переходя от комплексного представления к модульному можно записать: 
Таким образом, если четырехпроводная система напряжений симметрична, то при соединении звездой линейное напряжение в 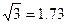 раза больше фазного напряжения и опережает его на угол
раза больше фазного напряжения и опережает его на угол 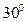
Для определения токов при симметричной нагрузке достаточно определить ток только в одной фазе. Зачастую в инженерной практике симметричная цепь изображается в виде однолинейной схемы. В трехпроводную цепь при соединении нагрузки  включают только симметричные трехфазные приемники (двигатели, электрические печи и др.).
включают только симметричные трехфазные приемники (двигатели, электрические печи и др.).
Вопрос 26
Несимметричная нагрузка. Сопротивление нейтрального провода, как и линейных проводов (рис.3.8.), примем равным нулю: 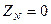 . Наличие несимметричной нагрузки приемника предполагает выполнение условия:
. Наличие несимметричной нагрузки приемника предполагает выполнение условия: 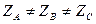
По аналогии со случаем симметричной нагрузки фазные напряжения можно записать так:
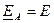 ;
; 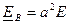 ;
; 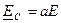 .
.
Токи в фазах приемника можно определить следующим образом:


Тогда ток в нейтральном проводе: 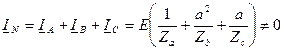
Благодаря нейтральному проводу (см. рис.3.8.)напряжения на каждой из фаз приемника при несимметричной нагрузке будут неизменными и равными соответствующим фазным напряжениям источника питания как по величине, так и по фазе. Т.е фазные и линейные напряжения приемника образуют симметричную систему. Однако токи в фазах будут разными.
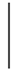 Следовательно: Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Следовательно: Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Поэтому в четырехпроводную сеть включают однородные приемники (например, лампы накаливания) и режим работы каждого такого приемника, находящегося под неизменным фазным напряжением источника питания, не будет зависеть от режима работы приемников, включенных в другие фазы.
Если сопротивлением нейтрального провода  не пренебречь, то при
не пренебречь, то при  фазные напряжения приемника не будут равны соответствующим напряжениям источника. В этом случае между нейтральными токами источника и приемника возникает напряжение
фазные напряжения приемника не будут равны соответствующим напряжениям источника. В этом случае между нейтральными токами источника и приемника возникает напряжение  , называемое напряжением относительно нейтрали или напряжением между нейтралями.
, называемое напряжением относительно нейтрали или напряжением между нейтралями.
Это напряжение определяется методом двух узлов.  , (3.10.)
, (3.10.)
где 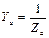 ;
; 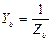 ;
; 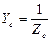 ;
; 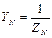 - комплексы проводимостей фаз и нейтрального провода.
- комплексы проводимостей фаз и нейтрального провода.
Зная 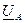 ,
, 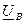 ,
, 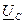 и
и  можно построить потенциальную диаграмму (рис.3.10.) и определить векторы фазных напряжений приемника
можно построить потенциальную диаграмму (рис.3.10.) и определить векторы фазных напряжений приемника 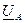 ,
, 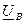 и
и 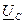 .
.
Комплексные значения этих напряжений можно определить воспользовавшись уравнениями, составленными по второму закону Кирхгофа
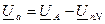 ;
; 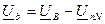 ;
;  . (3.11.)
. (3.11.)
Зная фазные напряжения приемника (3.11.) можно определить фазные токи:

 (3.12.)
(3.12.)
Ток в нейтральном проводе: 
При увеличении сопротивления нейтрального провода  эффективность его использования уменьшается, а именно, чем больше
эффективность его использования уменьшается, а именно, чем больше 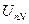 , тем больше фазные напряжения приемника отличаются от фазных напряжений источника (см. формулу 3.11).
, тем больше фазные напряжения приемника отличаются от фазных напряжений источника (см. формулу 3.11).
В случае обрыва нейтрального провода (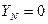 ) при несимметричной нагрузке величина
) при несимметричной нагрузке величина 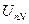 будет максимальной.
будет максимальной.
По этой причине плавкие предохранители в нейтральный провод не ставят, так как при перегорании предохранителя на фазах нагрузки могут возникнуть значительные перенапряжения. В нейтральный провод не вводят также выключатели (при выполнении лабораторной работы №5 тумблер в нейтральном проводе следует выключать только при соблюдении условия симметричной нагрузки в фазах приемника).
Вопрос 27
Для самого общего случая предположим, что фазы симметричного приемника  и нейтральный провод отсутствует (рис.3.11.а). В этом случае комплексные значения токов определяются как для однофазной цепи:
и нейтральный провод отсутствует (рис.3.11.а). В этом случае комплексные значения токов определяются как для однофазной цепи:  ,
, 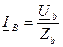 ,
,  . (3.13.)
. (3.13.)
Здесь 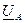 ,
, 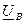 ,
, 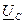 - напряжения на фазах нагрузки, соответствующие напряжениям точек “ a ”, “ b ” и “ c ”. Если потенциалы узлов “ N ” и “ n ” не равны, то напряжение между ними
- напряжения на фазах нагрузки, соответствующие напряжениям точек “ a ”, “ b ” и “ c ”. Если потенциалы узлов “ N ” и “ n ” не равны, то напряжение между ними 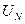 называется напряжением смещения нейтрали.
называется напряжением смещения нейтрали.
Напряжение на каждой фазе потребителя, соединяемого звездой, с учетом напряжения смещения 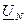 ,определяется следующим образом:
,определяется следующим образом: 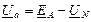 ;
;  ;
; 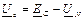 (3.14)
(3.14)
Найдем напряжение смещения нейтрали 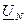 воспользовавшись методом двух узлов:
воспользовавшись методом двух узлов:
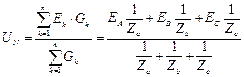 (3.15.)
(3.15.)
а) Для симметричного режима (когда  ;
;  ;
;  ;
; 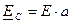 ) будем иметь:
) будем иметь:
 . (3.16.)
. (3.16.)
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 700; Нарушение авторских прав?; Мы поможем в написании вашей работы!