Билет 10. Символический метод, основанный на комплексной форме записи гармонических воздействий, позволяет расчеты цепей свести к составлению и решению алгебраических

Символический метод, основанный на комплексной форме записи гармонических воздействий, позволяет расчеты цепей свести к составлению и решению алгебраических уравнений, что существенно упрощает расчеты.

Возможность использования символического метода объясняется тем, что линейные электрические цепи не изменяют частоту гармонического воздействия. Это означает, что в таких цепях неизвестными параметрами токов и напряжений являются только амплитуды и фазы, которые однозначно определяются их комплексными амплитудами.

Закон Ома в комплексной форме. Закон Ома устанавливает связь между токами, напряжениями и сопротивлениями в элементах электрической цепи. Для резистивного, индуктивного и емкостного элементов имели

для R: i=(Um/R)sin(ωt+φi); φi= φu;

для L: i=(Um/ωL)sin(ωt+φi); φi= φu-π/2; X L= jωL; (3.31)

для С: i=UmωCsin(ωt+φi); φi= φu+π/2; X C=1/(jωC).

Связь между комплексными амплитудами токов Im и напряжений Um для элементов R,L и С можно определить согласно выражений (3.31), в которых заменим мгновенные значения токов i и амплитудные значения напряжений Um их комплексными амплитудамиIm и Um и будем иметь

дляR: I=Um/R;

дляL: I=Um/jωL; Um= jωLIm=j X L Im; (3.32)

дляС: I=Um jωC; Um=- j /(ωC)Im =-j X C Im.

Уравнения (3.32) справедливы и для комплексных действующих значений токов и напряжений:

дляR: I=U/R=UG;

для L: I=U/jXL=-jBL U; (3.33)

для С: I=jBC U= U/(-jXC),

где ;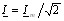

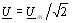
Законы Кирхгофа в комплексной форме. Первый и второй законы Кирхгофа в комплексной форме получаются путем замены мгновенных значений токов ik и напряжений uk в выражениях (1.22) и (1.23) их комплексными амплитудами Imk и Umk. Выполнив замену получим:

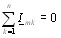(3.34)

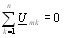(3.35)

Расчет цепи с последовательным соединением элементов символическим методом. Для цепи рис.3.4.а на основании выражения (3.35) можно составить следующее уравнение Um= UmR+UmL+Umс или с учетом (3.32)

Um=[R+j(ωL-l/ωC)]Im=(R+jX)Im=Z Im (3.36)

где Z - комплексное сопротивление цепи, которое равно

Z= R+jX=Z jφ =Z(cosφ+jsinφ) (3.37)

В выражении (3.37) Z - модуль, φ - аргумент (фаза) комплексного сопротивления, которые определяются формулами

;

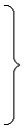
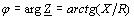. (3.38)

Расчет цепи с параллельным соединением элементов символическим методом. Для цепи (рис.3.5,а) имели выражение (3.27), которое с учетом (3.28) в комплексной форме примет вид

Im=[G-j(BL-BС)]Um =(G-jB)Um =Y Um, (3.39)

где величина Y есть комплексная проводимость цепи, которая определяется выражением

Y= G-jB=Ye-jφ=Y(cosφ-jsinφ) (3.40)

В выражении (3.40) полная проводимость цепи Y и фазовый сдвиг ф определяются формулами

Y=|Y|, φ=аrgY=аrсtg(В/G)

Расчет цепей в комплексной форме методом наложения (суперпозиции). Рассмотрим цепь, изображенную на рис.3.6,а, в которой необходимо определить ток i3.

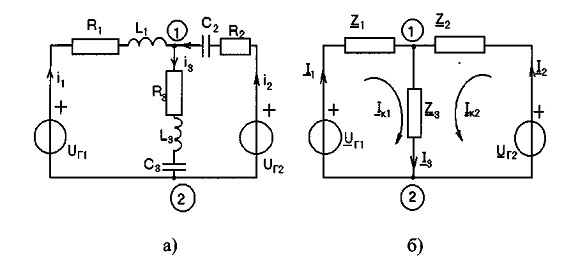
Рис. 3.6. Сложная электрическая цепь а) и ее эквивалентная схема б).

Заменим элементы ветвей исходной схемы их комплексными сопротивлениями Z1=R1+jωL1; Z2=R2-j(1/ωC2); Z3=R3+j(ωL3-(1/ωС3), а источники напряжения и токи их комплексными значениями и получим эквивалентную схему рис.3.6,б. Сравнение схем, изображенных на рис.3.6.б и рис.1.18,б показывает их одинаковую топологию, что позволяет определить ток i3 по методам, изложенным в § 1.4.4.

Расчет цепей в комплексной форме методом контурных токов. Согласно §1.4.5 для схемы рис.3.6,б можно составить следующую систему уравнений

;

,

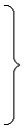
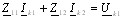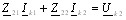где Z11=Z1+Z3; Z22=Z2+Z3; Z12=Z21=Z3; Uk1=UГ1; Uk2=UГ2.

Используя выражения (1.41) и (1.42) получаем

Ik1=Uk1(Δ11/ ΔZ)+ Uk2(Δ21/ ΔZ);

Ik2=Uk1(Δ12/ ΔZ)+ Uk2(Δ22/ ΔZ),

где ΔZ= 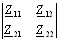– определитель системы.

Δ 11, Δ12, Δ21, Δ22 - алгебраические дополнения определителя ΔZ. 3ная контурные токи Ik1 и Ik2, определяем токи в ветвях схемы I1=Ik1; I2=Ik2; I3=Ikl+Ik2.

Расчет цепей в комплексной форме методом эквивалентного генератора. Определим ток i3 используя методику §1.4.6. Для этого разомкнем ветвь с Z3 (рис.3.6,б) и определим напряжение холостого хода Uxx=UГ2-I2Z2 и эквивалентное сопротивление цепи ZЭ=Z1Z2/(Z1+Z2). Зная напряжение холостого хода и эквивалентное сопротивление цепи находим ток в цепи по формуле: I3=Uxx/(ZЭ+Z3). Примем, что угловая частота источников гармонических колебаний UГ1 и UГ2 равна ω, тогда мгновенное значение тока i3=Im3sin(ωt+φ3), Im3=|I3|√2, φ3=arg I3, I3=I3e jφ3.

· Тиристор

· Симистор

Дата добавления: 2015-05-06