Сумматоры. Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел

Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.

Классификация сумматоров:

В зависимости от формы представления информации различают сумматоры аналоговые и цифровые.

По способу реализации

• механические
• электромеханические
• электронные
• пневматические

По архитектуре

• четвертьсумматоры — бинарные (двухоперандные) сумматоры по модулю без разряда переноса, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма по модулю;
• полусумматоры — бинарные (двухоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (старший разряд);
• полные сумматоры — тринарные (трёхоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (более старший разряд). Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления.^{[источник не указан 660 дней]}

По способу действия

• Последовательные (одноразрядные), в которых обработка разрядов чисел ведётся поочерёдно, разряд за разрядом, на одном и том же одноразрядном оборудовании;
• Параллельные (многоразрядные), в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование;

По способу организации переноса

• С последовательным переносом;
• С параллельным переносом;
• С условным переносом;
• С групповым переносом.

Двоичный сумматор

имеет три входа (два слагаемых и перенос из предыдущего разряда) и два выхода (суммы и переноса в следующий разряд).

Таблица истинности одноразрядного сумматора имеет вид, представленный в табл. 1.

Таблица 1

ai	bi	ci–1	ci	si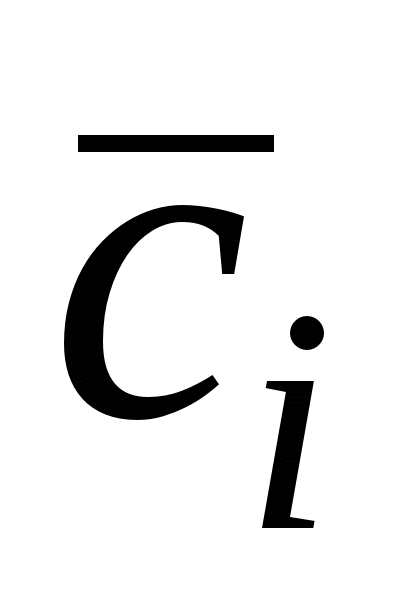
0	0	0	0	0	1
0	0	1	0	1	1
0	1	0	0	1	1
0	1	1	1	0	0
1	0	0	0	1	1
1	0	1	1	0	0
1	1	0	1	0	0
1	1	1	1	1	0

Как видно из таблицы, совокупность сигналов c_i и s_i по сути является двухзначной суммой трёх чисел a_i, b_i и c_i–1

Аналитические выражения функций суммы S (от англ. sum) и переноса С (от англ. Carry) имеют вид

; .

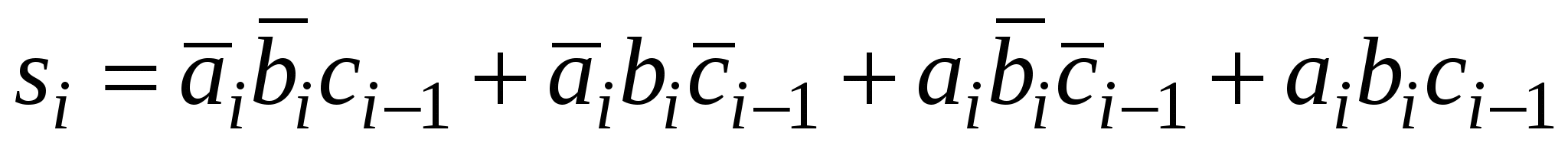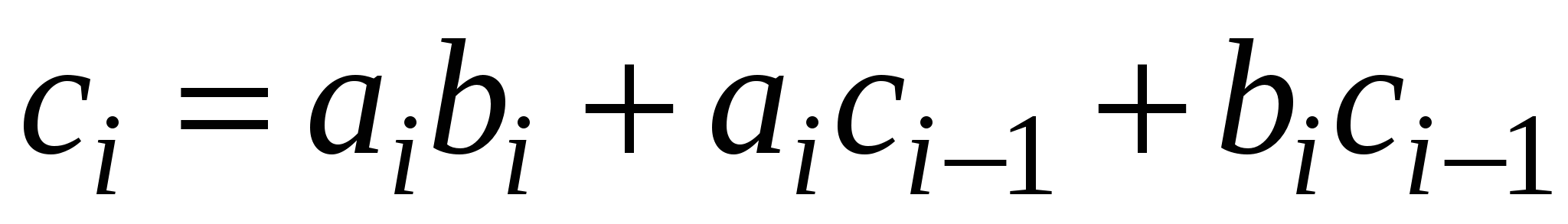Дата добавления: 2015-05-06