Теоретическая часть. Наиболее широкое применение в электротехнике и радиотехнике получили переменные напряжения и токи, являющиеся периодическими функциями времени

Наиболее широкое применение в электротехнике и радиотехнике получили переменные напряжения и токи, являющиеся периодическими функциями времени. Электрические цепи, в которых э. д. с., напряжения и токи изменяются во времени по синусоидальному закону, называются цепями переменного синусоидального тока. Значение переменного тока в любой заданный момент времени называют мгновенным током i. Направление переменного тока, для которого его мгновенные значения i положительны, считается положительным.

Процессы, наблюдаемые в линейных цепях с синусоидально изменяющимися токами и напряжениями, являются простейшими - к ним можно свести процессы, наблюдаемые в цепях с несинусоидально изменяющимися напряжениями и токами. Поэтому анализ более сложных процессов, связанных с прохождением несинусоидальных и непериодических токов, обычно проводят с помощью приемов, разработанных в теории цепей синусоидального тока.

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим. Следует также указать на то, что в процессе эксплуатации электрических цепей при иных формах тока из-за возникновения э. д. с. самоиндукции на отдельных участках цепи могут создаваться значительные перенапряжения. Кроме того, расчет цепей с синусоидальными э. д. с., напряжениями и токами значительно проще, чем расчет цепей с несинусоидальными величинами.

В энергетике, как правило, применяют синусоидальные токи, которые обычно называют переменными. В связи, электронике, телемеханике используют несинусоидальные токи, например импульсные. Итак, переменные э д. с., напряжения и токи могут быть весьма разнообразны, однако среди них наиболее часто применяют периодические.

Периодическими называются такие э. д. с., напряжения и токи, мгновенные значения которых повторяются в одинаковой последовательности через равные промежутки времени, изображены на рисунке 2а.

Наименьший промежуток времени, в течение которого мгновенные значения переменного тока i принимают все возможные значения, как положительные, так и отрицательные, называется периодом Т. Число периодов переменного тока в 1 с называется частотой: f = 1 / Т.Единицей частоты служит герц (Гц), равный одному периоду в секунду: 1 Гц = 1 с^-1.

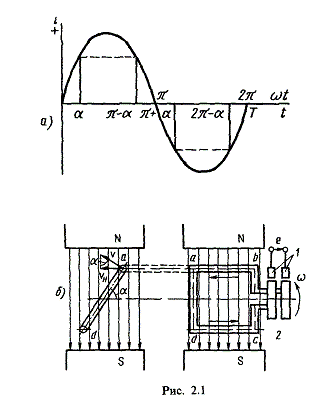
Рисунок 2. Генератор синусоидальной э.д.с.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной э. д. с. Простейшим генератором синусоидальной э. д. с. может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω, изображен на рисунке 2. Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции э. д. с. е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v_н:

e = Blv_н (1)

где В и l - постоянные величины, a v_н - переменная, зависящая от угла α. Выразив скорость v _н через линейную скорость катушки v, получим

e = Blvsinα (2)

В выражении (2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.

Если угол α = π/2, то произведение Blv в формуле (2) есть максимальное (амплитудное) значение наведенной э. д. с. E_m = Blv. Поэтому выражение (2) можно записать в виде

e = E_msinα (3)

Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (3) переписать в виде

e = E_msinωt (4)

где е - мгновенное значение э. д. с. в катушке; α = ωt - фаза, характеризующая значение э. д. с. в данный момент времени.

ПУСТО

Рисунок 3. Графики мгновенных значений э.д.с.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.

Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе - время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рисунке 3 построены графики мгновенных значений э. д. с. е и е'.

Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки,как представлено на рисунке 2, происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рисунка 3 видно, что ωТ = 2π, откуда

ω = 2π / T = 2πf (5)

Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рисунке 2 э. д. с. е и е' можно описать выражениями

e = E_msinωt; e' = E'_msin(ωt + ψ_e').

Здесь ωt и ωt + ψ_e' - фазы, характеризующие значения э. д. с. e и e' в заданный момент времени; ψ_e' - начальная фаза, определяющая значение э. д. с. е' при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ_e = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ,как на рисунке 3, откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу - вправо.

ПУСТО

Рисунок 4. Сдвиг фаз

ПУСТО

Рисунок 5. Графики синусоидальных напряжения и тока

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ, как показано на рисунке 4.

Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что онисовпадают по фазе.

Для синусоидальных значений напряжения и тока, графики которых представлены на рисунке 5, угол сдвига фаз равен нулю (φ = 0) и начальные фазы, естественно, также равны нулю (ψ_i = ψ_u = 0). Такие величины описываются выражениями

u = U_msinωt; i = I_msinωt.

Синусоидальные напряжение и ток, графики которых представлены на рисунке 4, описываются следующим образом:

u = U_msin(ωt + ψ_u); i = I_msin(ωt + ψ_i), (6)

причем угол сдвига фаз между током и напряжением,как показано на рисунке 4,в этом случае φ = ψ_u - ψ_i.

Уравнения (6) можно записать иначе:

u = U_msin(ωt + ψ_i + φ); i = I_msin(ωt + ψ_u - φ),

поскольку ψ_u = ψ_i + φ и ψ_i = ψ_u - φ.

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).

Совокупность векторов, изображающих синусоидальные э. д. с., напряжение и ток одной частоты, называют векторными диаграммами, которые изображены на рисунке 6. Построение векторных диаграмм наиболее рационально начинать с момента, когда начальное положение вектора определяется начальной фазой. При начальной фазе ψ = 0 вектор в начальный момент располагается по оси абсцисс. На рисунке 6, а показаны векторы напряжения u и тока i, изображенных синусоидами на рисунке 5.

Рисунок 6. Векторные диаграммы

Рисунок 7. Сложение векторов синусоидальных токов

В этом случае при t = 0 их мгновенные значения равны нулю. На рисунке 6, б изображены векторы, соответствующие синусоидам напряжения и и тока i, представленных на рисунке 4, для которых начальные фазы различны и не равны нулю. Для этих величин при t = 0 их мгновенные значения не равны нулю.

Применение векторных диаграмм делает анализ электрической цепи наглядным. В этом методе сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием их векторов. Так, если необходимо сложить два синусоидальных тока одинаковой частоты i₁ = I_1msin(ωt + ψ₁) и i₂ = I_2msin(ωt + ψ₂) то надо в системе прямоугольных координат построить два вектора, длина которых в выбранном масштабе равна соответственно амплитудам токов I_1т и I_2т, а направления определяются начальными фазами ψ₁ и ψ₂ . Пример сложения векторов приведен на рисунке 7. Если эти векторы вращать с одинаковой угловой скоростью, то их взаимное расположение не изменится и угол сдвига фаз между ними α останется постоянным, равным α = ψ₁ - ψ₂. Поэтому для любого момента времени мгновенное значение суммарного тока i равно сумме мгновенных значений токов i₁ и i ₂, т. е. сумме проекций векторов I_1т и I_2т на ось ординат i = i₁ + i₂.

А так как известно, что сумма проекций нескольких векторов на одну и ту же ось равна проекции их геометрической суммы на ту же ось, то вектор I_m будет представлять собой геометрическую сумму векторов I_1m и 1_2т, т. е. соответствовать суммарному синусоидальному току i = I_msin(ωt + ψ); его длина в выбранном масштабе равна амплитуде этого тока, а угол ψ представляет его начальную фазу.

Это справедливо и для случая сложения и вычитания нескольких синусоидальных величин, причем при вычитании векторов производят их сложение, а вычитаемый вектор берут с обратным знаком. Запись геометрического сложения вращающихся векторов производится так же, как и для обычных векторов, находящихся в состоянии покоя.

Дата добавления: 2015-05-06