Фильтр Баттерворта

АЧХ фильтра Баттерворта в пределах полосы пропускания близка к равномерной и ее называют максимально плоской. Наклон переходного участка 6 дБ/окт на полюс или на порядок. Фильтр имеет нелинейную ФЧХ, т.е. время, которое требуется для прохождения сигнала через фильтр зависит от частоты. Поэтому ступенчатый сигнал или импульс, поданный на вход, вызывает выброс на его выходе.

Используется тогда, когда нужно иметь одинаковый коэффициент усиления 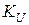для всех частот в полосе пропускания.

- ослабление 6дБ/окт (20дБ/дек)

Фильтр Чебышева

АЧХ имеет волнообразные зубцы в полосе пропускания и равномерна в полосе подавления. Количество зубцов тем больше, чем выше его порядок. Амплитуда зубцов может быть задана при конструировании фильтра и обычно устанавливается на уровне 0.5,1,2 или 3дБ причем увеличение допустимой амплитуды зубцов позволяет получить более крутой наклон характеристики фильтра на переходном участке.

(или )

где n – порядок фильтра (равен количеству полюсов)

ε = (0÷1) - постоянная, характеризующая неравномерность характеристики фильтра в полосе пропускания.

Неравномерности δ=0,5 дБ соответствует величина ε = 0,3493, неравномерности δ=3 дБ -

ε = 0, 9976.

Если n =1 и дБ/дек

Используется, если желательно иметь очень крутой наклон на переходном участке. Имеет неравномерность в полосе пропускания и еще более нелинейную ФЧХ по сравнению с фильтром Баттерворта.

Запаздывание по фазе еще более нелинейно, чем у фильтра Баттерворта.

Чем выше порядок и выше неравномерность в полосе пропускания, тем более нелинейная его ФЧХ и тем больше выбросы мы получим подавая на выход такого фильтра ступеньки и импульсы.

Фильтры Чебышева используются там, где необходимо получить максимальный наклон переходного участка, а неравномерность не имеет значения.

Фильтр Бесселя

Фильтр с линейной фазой или постоянной задержкой, т.е. запаздывание по фазе выходного сигнала в радианах линейно вырастает с частотой. Почти не дают выброса импульсного сигнала. Имеют наклон переходного участка менее 6 дБ/окт. Наиболее подходящий для фильтрации импульсных сигналов.

Существуют обратный фильтр Чебышева равномерный в полосе пропускания и с зубцами в полосе подавления; эллиптический (фильтр Кауэра) с очень крутым наклоном на переходном участке, но не равномерный в полосе подавления; и параболический с очень хорошей импульсной характеристикой.

Коэффициент затухания α определяет форму характеристики на переходном участке и вид выброса характеристики в полосе пропускания вблизи переходного участка.

Одна и та же схема в зависимости от выбора значений ее компонентов может действовать как фильтр Бесселя, Баттерворта или Чебышева и форма ЧХ фильтра определяется коэффициентом затухания.

Добротность Q связывает среднюю частоту полосы пропускания и ее ширину на уровне 3дБ.

Для активных фильтров .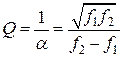

Коэффициент усиления (передачи) в полосе пропускания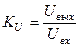

Чувствительностью одного из параметров фильтра по отношению к другому его параметру называется отношение величины изменения первого параметра к величине изменения второго, если изменение 2-го параметра вызывает изменение 1-го.

значит, что ω_о уменьшилось на 0,5%, при увеличении R1 на 1%.

Дата добавления: 2015-05-06