Краткие теоретические сведения. Порядок оформления отчета

ЦЕПИ ПОСТОЯННОГО ТОКА.

Лабораторная работа №1

Порядок оформления отчета

1. Краткое содержание задания.

2. Электрические схемы измерений.

3. Таблицы измерений и вычислений.

4. Расчеты всех требуемых параметров с приведением соответствующих формул.

5. Графики и векторные диаграммы.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение

высшего профессионального образования

Московский государственный университет

пищевых производств

Кафедра «Автоматика и электротехника»

Отчет по лабораторной работе №____

____________________________________

( наименование работы)

Работу выполнил

Студент гр. _______

____________________

(Ф.И.О.)

Работу принял

Преподаватель

____________________

(Ф.И.О.)

Москва 20____

Цель работы: сопоставить основные теоретические положения, свойственные цепям постоянного тока с экспериментальными данными.

Электрической цепью постоянного тока называется совокупность соединенных между собой элементов цепи: источников (генераторов постоянного тока, аккумуляторов и т.д.), приемников электрической энергии (реостатов, ламп накаливания и т.д.) и связывающих их соединительных проводов.

Для определенности будем называть источники электрической энергии генераторами, а совокупность приемников электрической энергии нагрузкой.

Для того, чтобы упростить рассмотрение процессов в электрической цепи, ее заменяют расчетной схемой или идеализированной цепью и пользуются понятиями элементов схемы: электродвижущей силой (ЭДС) Е и внутренним сопротивлением R ₀ генератора и сопротивлением нагрузки R. Сопротивлением соединительных проводов обычно пренебрегают, т.е. считают его равным нулю. Таким образом, простейшая цепь постоянного тока состоит из генератора (Е – ЭДС генератора, R ₀ - внутреннее сопротивление генератора) и нагрузки R, подсоединенной к зажимам генератора «А» и «В» (рис.1) с помощью соединительных проводов.

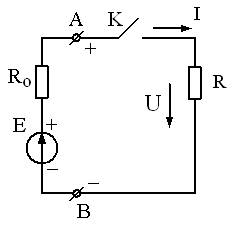
Рис.1. Схема простейшей цепи постоянного тока.

Совокупность нагрузки и соединительных проводов называется внешней цепью в отличие от полной цепи постоянного тока, включающей в себя и генератор. Ключ К предназначен для подключения или отключения нагрузки от генератора.

Направление действия ЭДС принимают от низшего потенциала к высшему. Зажим генератора с более высоким потенциалом называется положительным и обозначается знаком «+», а зажим с более низким потенциалом называется отрицательным и обозначается знаком «−».

На схемах источники ЭДС обозначаются кружком со стрелкой внутри него, указывающей направление действия ЭДС 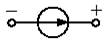, либо знаком . ЭДС измеряется в вольтах (В). Направление тока внутри генератора совпадает с направлением действия ЭДС, т.е. от зажима«−» к зажиму «+». Во внешней цепи (рис.1) ток направлен от зажима «А» (+) к зажиму «В» (−), т.е. от точки с более высоким потенциалом φ _А к точке с более низким потенциалом φ _В. Это направление тока принято считать положительным.

ЭДС генератора определяют в режиме холостого хода (ключ К разомкнут, ток в цепи отсутствует) как напряжение на его зажимах. Это напряжение называется напряжением холостого хода U _хх , т.е. Е = U _хх.

Если замкнуть ключ К и таким образом присоединить нагрузку R к зажимам генератора (рис.1), то в замкнутом контуре возникает ток I, при этом напряжение на зажимах генератора не будет равно ЭДС вследствие падения (потери) напряжения внутри генератора Δ U _Г = I ∙ R ₀. Таким образом, напряжение на зажимах генератора будет равно

U = E – Δ U _Г = E – I ∙ R ₀ = U _хх – I ∙ R ₀. (1)

Ток в цепи зависит от сопротивления нагрузки R и внутреннего сопротивления генератора R ₀.

I = 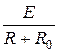= 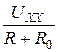. (2)

Из выражений (1) и (2) следует, что чем меньше сопротивление нагрузки R, тем больше ток I и потери напряжения на внутреннем сопротивлении генератора Δ U _Г и тем меньше напряжение на зажимах генератора U.

Зависимость напряжения на зажимах генератора от величины тока в цепи называется внешней характеристикой генератора

Типичная внешняя характеристика генератора U = f (I) показана на рис. 2.

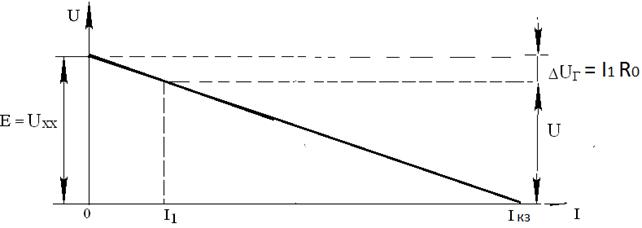
Рис.2. Внешняя характеристика генератора

Пренебрегая сопротивлением соединительных проводов, считаем, что напряжение на зажимах генератора приложено к сопротивлению нагрузки (рис.1). Если сопротивление нагрузки равно нулю (R = 0), то такой режим работы называется режимом короткого замыкания, при котором ток в цепи принимает максимальное значение I _КЗ = 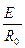, а напряжение на зажимах генератора U = 0, (см. рис. 2).

Полная мощность генератора определяется как

Р ₁= I ²∙(R ₀ + R) = 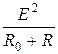= 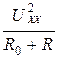(3)

Полезная мощность генератора определяется как

Р ₂ = 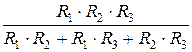= = 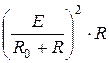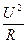(4)

Коэффициент полезного действия генератора равен

η = 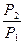= = 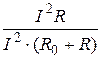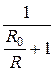. (5)

При анализе электрических цепей используются понятия ветвь, узел и контур.

Ветвью называется участок электрической цепи, по которому проходит один и тот же ток.

Узлом называется точка соединения трех и более ветвей.

Контуром называется одна или несколько ветвей, образующих замкнутую электрическую цепь.

Элемент электротехнической цепи, специально изготавливаемый для получения заданного сопротивления, называется резистором. Термины «сопротивление» и «резистор» часто используются как слова синонимы.

Различают параллельное, последовательное и смешанное соединение сопротивлений (резисторов).

При последовательном соединении через все резисторы протекает один и тот же ток. При таком соединении общее сопротивление внешней цепи (нагрузки) равно сумме сопротивлений всех резисторов, т.е. R = .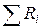

Таким образом, чем больше сопротивлений подключено последовательно, тем больше общее сопротивление цепи.

При параллельном соединении все резисторы находятся под одним и тем же напряжением. При таком соединении общая проводимость внешней цепи равна сумме проводимостей всех резисторов, т.е. Y = 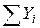. Из этого выражения можно получить формулу для расчета общего (эквивалентного) сопротивления внешней цепи R, зная количество ветвей в ней. Так, для схемы из двух ветвей R ₁ и R ₂ имеем

Y = Y ₁ + Y ₂, т.е. 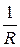= 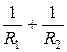, откуда R _Э = 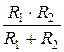(6)

Для схемы, состоящей из двух трех ветвей (R ₁, R ₂ и R ₃) имеем

R _Э = 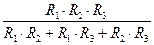(7)

Можно показать, что чем больше сопротивлений подключено параллельно, тем меньше общее (эквивалентное) сопротивление цепи. Так для трех одинаковых сопротивлений R₁ = R₂ = R₃ = R из выражения (7) получаем

R _Э =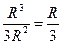

При смешанном соединении часть сопротивлений соединена параллельно, а другая часть последовательно.

Вычисление мощности Р, выделяющейся на сопротивлении R, можно провести по одной из следующих формул:

Р = UI = I²R = ,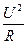

где U – напряжение, приложенное к сопротивлению R,

I – ток, протекающий по сопротивлению R.

Основными теоретическими положениями, подлежащими сопоставлению с экспериментальными данными в соответствии с целью работы, являются первый и второй законы Кирхгофа и уравнение баланса мощностей.

Согласно первому закону Кирхгофа: алгебраическая сумма токов, сходящихся в любом узле электрической цепи равна нулю, т.е.

Σ I = 0 (8)

Этот закон также может быть сформулирован следующим образом: сумма токов, притекающих к узлу, равна сумме токов, уходящих от узла.

Согласно второму закону Кирхгофа: алгебраическая сумма ЭДС, действующих во всяком замкнутом контуре, равна алгебраической сумме напряжений, приложенных ко всем сопротивлениям, входящим в этот контур, т.е.

Σ Е = Σ I ∙ R (9)

Уравнение баланса мощностей в любой электрической цепи формулируется в соответствии с правилом: алгебраическая сумма мощностей, развиваемых всеми источниками энергии, равна алгебраической сумме мощностей, выделяющихся на всех сопротивлениях электрической цепи, т.е.

Σ Е ∙ I = Σ I ²∙ R (10)

Дата добавления: 2015-05-06