Теоретическая часть. Изучение атомных спектров послужило ключом к познанию строения атомов

Изучение атомных спектров послужило ключом к познанию строения атомов. Прежде всего, было замечено, что линии в спектрах атомов расположены на беспорядочно, а объединяются в группы или, как их называют, серии линий. Отчетливее всего это обнаруживается в спектре простейшего атома водорода. На рисунке 1 представлена часть спектра атомарного водорода в видимой и близкой ультрафиолетовой области. Символами 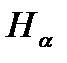, , 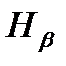, 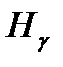обозначены видимые линии. 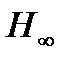указывает границу серии. Очевидно, что линии располагаются в определенном порядке.

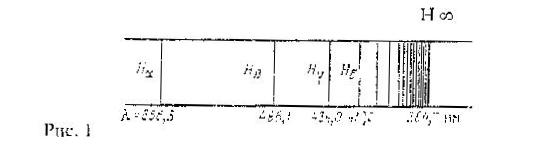
Расстояние между линиями закономерно убывает по мере перехода от более длинных волн к более коротким. Швейцарский физик Бальмер (1885) обнаружил, что длины волн этой серии, линий водорода могут быть точно представлены формулой:

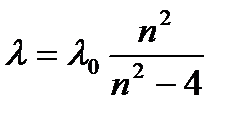, (1)

где 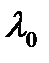- константа;

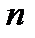- целое число, принимающее значение 3, 4, 5 и т.д.

Если перейти в (1) от длины волны к частоте, получится формула:

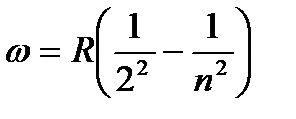, (2)

где 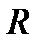- константа, называемая в честь шведского спектроскописта постоянной Ридберга. Она равна:

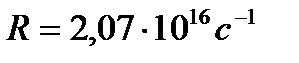(3)

Формула (2) называется формулой Бальмера, а соответствующая серия спектральных линий водородного атома серией Бальмера. Дальнейшие исследования показали, что в спектре водорода имеются еще несколько серий. В ультрафиолетовой части спектра находится серия Лаймана, остальные серии лежат в инфракрасной области. Линии этих серий могут быть представлены в виде формул, аналогичных (2):

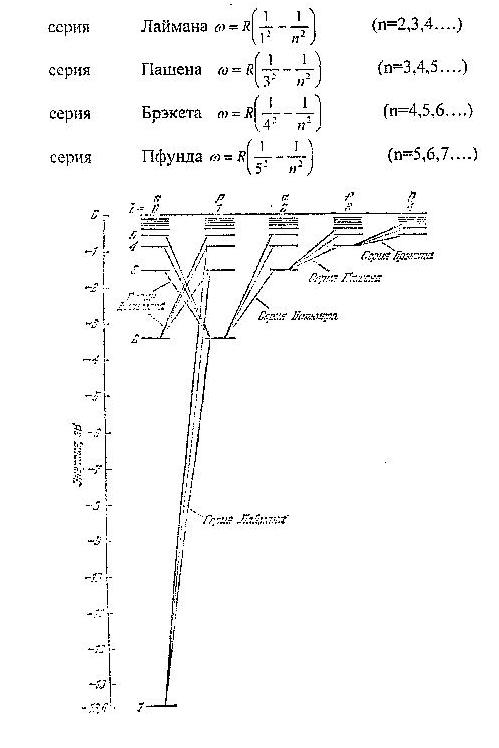
Частоты всех линий спектра водородного атома можно представить одной формулой:

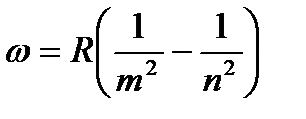, (4)

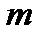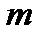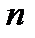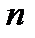где имеет значение 1 для серии Лаймана, 2 – для серии Бальмера и т.д. При заданном число принимает все целочисленные значения, начиная с . При возрастании частота линии в каждой серии стремится к предельному значению 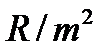, которое называется границей серии (на рисунке 1 символом 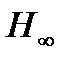отмечена граница серии Бальмера).

Возьмем ряд значений выражения :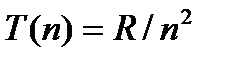

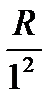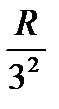, , … (5)

Частота любой линии спектра водорода может быть представлена в виде разности двух чисел ряда (5). Эти числа называют спектральными термами или просто термами. Так, например, частота первой линии серии Бальмера равна T(2) второй линии серии Пфунда T(0) T(7) и т.д. Изучение спектров других атомов показало, что частоты линий и в этом случае могут быть представлены в виде разностей двух термов (комбинационный принцип Ритца):

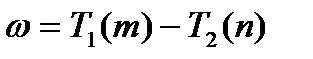(6)

Однако терм 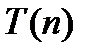обычно имеет более сложный вид, чем для водородного атома. Кроме того, первый и второй члены формулы (6) берутся из различных рядов термом. Теоретическое обоснование эмпирической формулы Бальмера дает квантомеханический подход. В рамках данного подхода для атома водорода записывается уравнение Шредингера:

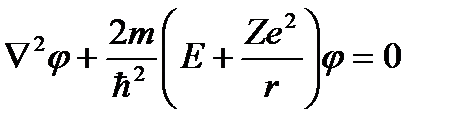(7)

Далее ищутся решения данного уравнения на собственные значения. Уравнение (7) имеет однозначные, непреревные, конечные решения при дискретных отрицательных значениях энергии :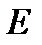

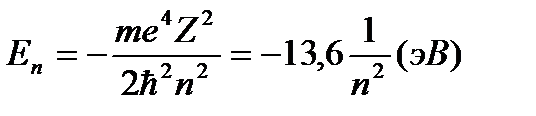
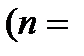1, 2, 3, 4…) (8)

Число 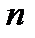, фигурирующее в формуле (8), называется главным квантовым числом.

Сравнивая (8) с бальмеровским видом записи спектральных термов, приходим к выводу, что совокупность спектральных термов отображает закон квантования энергетического спектра атома водорода, а постоянная Ридберга для атома водорода может быть представлена в виде:

(9)

Дата добавления: 2015-05-06