Основные формулы

ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

· Напряженность электрического поля

E = F / Q,

где F — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.

· Сила, действующая на точечный заряд Q, помещенный в электрическое поле,

F = Q E.

· Поток вектора напряженности Е электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле,

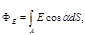или ,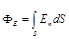

где a — угол между вектором напряженности Е и нормалью n к элементу поверхности; d S — площадь элемента поверхности; E_n — проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле,

Ф _E=ЕS cosa.

· Поток вектора напряженности Е через замкнутую поверхность

,

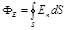где интегрирование ведется по всей поверхности.

· Теорема Остроградского — Гаусса. Поток вектора напряженности Е через любую замкнутую поверхность, охватывающую заряды Q_l, Q₂,..., Q_n,

,

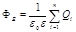где 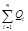— алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; п — число зарядов.

· Напряженность электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда,

.

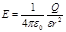Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд Q, на расстоянии r от центра сферы:

а) внутри сферы (r<.R)

E =0;

б) на поверхности сферы (r = R)

;

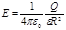в) вне сферы (r>R)

.

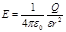· Принцип суперпозиции (наложения) электрических полей, согласно которому напряженность Е результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:

Е = E ₁ + Е ₂ +...+ Е _n.

В случае двух электрических полей с напряженностями Е ₁ и Е ₂ модуль вектора напряженности

,

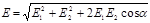где a — угол между векторами E ₁ и E ₂.

· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянии r от ее оси,

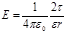, где t — линейная плотность заряда.

Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити (цилиндра):

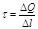
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

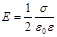
где s — поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:

.

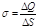· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью о заряда (поле плоского конденсатора)

.

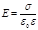Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

· Электрическое смещение D связано с напряженностью E электрического поля соотношением

D =e ₀ e E.

Это соотношение справедливо только дляизотропных диэлектриков.

· Поток вектора электрического смещения выражается аналогично потоку вектора напряженности электрического поля:

а) в случае однородного поля поток сквозь плоскую поверхность

;

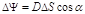б) в случае неоднородного поля и произвольной поверхности

,

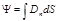где D_n — проекция вектора D на направление нормали к элементу поверхности, площадь которой равна d S.

· Теорема Остроградского — Гаусса. Поток вектора электрического смещения сквозь любую замкнутую поверхность, охватывающую заряды Q₁, Q₂,..., Q_n,

,

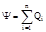где п —число зарядов (со своим знаком), заключенных внутри замкнутой поверхности.

· Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру 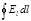, где E_l— проекция вектора напряженности Е в данной точке контура на направление касательной к контуру в той же точке.

В случае электростатического поля циркуляция вектора напряженности равна нулю:

.

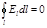Примеры решения задач

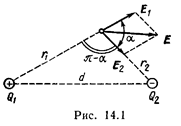Пример 1. Электрическое поле создано двумя точечными зарядами: Q₁ =30 нКл и Q₂ = –10 нКл. Расстояние d между зарядами равно 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r₁ =15 см от первого и на расстоянии r₂ =10 см от второго зарядов.

Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность Е электрического поля в искомой точке может быть найдена как векторная сумма напряженностей E ₁ и Е ₂ полей, создаваемых каждым зарядом в отдельности: E = E ₁ + E ₂.

Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны

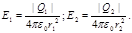(1)

Вектор E ₁ (рис. 14.1) направлен по силовой линии от заряда Q₁, так как заряд Q₁ >0; вектор Е ₂ направлен также по силовой линии, но к заряду Q₂, так как Q₂ <0.

Модуль вектора Е найдем по теореме косинусов:

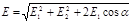, (2)

где угол a может быть найден из треугольника со сторонами r₁, r₂ и d:

.

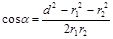В данном случае во избежание громоздких записей вычислим отдельно значение cosa. По этой формуле найдем

cosa =0,25.

Подставляя выражения E₁ и E₂ а по формулам (1) в равенство (2) и вынося общий множитель 1/(4pe ₀) за знак корня, получаем

.

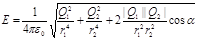Подставив значения величин p, e ₀, Q₁, Q₂, r₁ -, r₂ и a в последнюю формулу и произведя вычисления, найдем

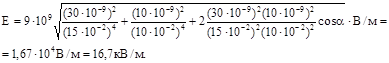
Пример 2. Электрическое поле создано двумя параллельными бесконечными заряженными плоскостями с поверхностными плотностями заряда s ₁ =0,4 мкКл/м² и s ₂ =0,1 мкКл/м². Определить напряженность электрического поля, созданного этими заряженными плоскостями.

Решение. Согласно принципу суперпозиции, поля, создаваемые каждой заряженной плоскостью в отдельности, накладываются друг на друга, причем каждая заряженная плоскость создает электрическое поле независимо от присутствия другой заряженной плоскости (рис. 14.2).

Напряженности однородных электрических полей, создаваемых первой и второй плоскостями, соответственно равны:

; .

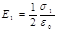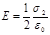Плоскости делят все пространство на три области: I, II и III. Как вид но из рисунка, в первой и третьей областях электрические силовые линии обоих полей направлены в одну сторону и, следовательно, напряженности суммарных полей Е^(I) и E ^(III) в первой и третьей областях равны между собой и равны сумме напряженностей полей, создаваемых первой и второй плоскостями: Е^(I)= E ^(III)= E₁+E₂, или

Е^(I)= E ^(III) = .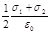

Во второй области (между плоскостями) электрические силовые линии полей направлены в противоположные стороны и, следовательно, напряженность поля E^(II) равна разности напряженностей полей, создаваемых первой и второй плоскостями: E^(II)=|E₁-E₂|, или

.

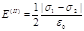Подставив данные и произведя вычисления, получим

E^(I)=E^(III)=28,3кВ/м=17 кВ/м.

Картина распределения силовых линий суммарного поля представлена на рис. 14.3.

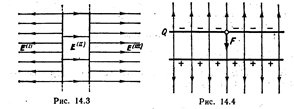
Пример 3. На пластинах плоского воздушного конденсатора находится заряд Q =10 нКл. Площадь S каждой пластины конденсатора равна 100 см² Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.

Решение. Заряд Q одной пластины находится в поле, созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила (рис. 14.4)

F=E₁Q,, (1)

где E₁ — напряженность поля, создаваемого зарядом одной пластины. Но 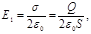где s – поверхностная плотность заряда пластины.

Формула (1) с учетом выражения для E₁ примет вид

F = Q² /(2e ₀S).

Подставив значения величин Q, e ₀ и S в эту формулу и произведя вычисления, получим

F =565 мкН.

Пример 4. Электрическое поле создано, бесконечной плоскостью, заряженной с поверхностной плотностью s = 400 нКл/м ², и бесконечной прямой нитью, заряженной с линейной плотностью t=100 нКл/м. На расстоянии r =10 см от нити находится точечный заряд Q =10 нКл. Определить силу, действующую на заряд, ее направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости.

Решение. Сила, действующая на заряд, помещённый в поле,

F=EQ, (1)

где Е — напряженность поля в точке, в которой находится заряд Q.

Определим напряженность Е поля, создаваемого, по условию задачи, бесконечной заряженной плоскостью и бесконечной заряженной нитью. Поле, создаваемое бесконечной заряженной плоскостью, однородно, и его напряженность в любой точке

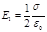. (2)

Поле, создаваемое бесконечной заряженной линией, неоднородно. Его напряженность зависит от расстояния и определяется по формуле

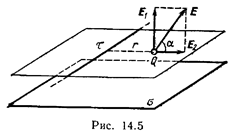
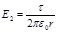. (3)

Согласно принципу суперпозиции электрических полей, напряженность поля в точке, где находится заряд Q, равна векторной сумме напряженностей E ₁ и Е ₂ (рис. 14.5): E = E ₁ + E ₂. Так как векторы E ₁ и Е ₂ взаимно перпендикулярны, то

.

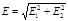Подставляя выражения E₁ и E₂ по формулам (2) и (3) в это равенство, получим

,

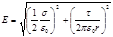или .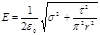

Теперь найдем силу F, действующую на заряд, подставив выражение Е в формулу (1):

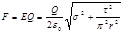. (4)

Подставив значения величин Q, e ₀, s, t, p и r в формулу (4) и сделав вычисления, найдем

F =289 мкН.

Направление силы F, действующей на положительный заряд Q, совпадает с направлением вектора напряженности Е поля. Направление же вектора Е задается углом a к заряженной плоскости. Из рис. 14.5 следует, что

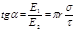, откуда .

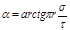Подставив значения величин p, r, s и t в это выражение и вычислив, получим

a=51°3¢

Пример 5. Точечный заряд Q =25 нКл находится в ноле, созданном прямым бесконечным цилиндром радиусом R= 1 см, равномерно заряженным с поверхностной плотностью s=2 мкКл/м². Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r =10 см.

Решение. Сила, действующая на заряд Q, находящийся в поле,

F=QE, (1)

где Е — напряженность поля в точке, в которой находится заряд Q.

Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра

E =t/(2pe ₀r), (2)

где t — линейная плотность заряда.

Выразим линейную плотность t через поверхностную плотность s. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q₁ двумя, способами:

Q₁=sS=s2pRl и Q ₁ =t l.

Приравняв правые части этих равенств, получим t l =2p Rls. После сокращения на l найдем t=2p Rs. С учетом этого формула (2) примет вид E=Rs/(e₀r). Подставив это выражение Е в формулу (1), найдем искомую силу:

F=QsR/(e₀r). (3)

Так как R и r входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах.

Выполнив вычисления по формуле (3), найдем

F =25×10^-9×2×10^-6×10^-2/(8,85×10^-12×10×10^-2)H==565×10^-6H=565мкH.

Направление силы F совпадает с направлением вектора напряженности Е, а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.

Пример 6. Электрическое поле создано тонкой бесконечно длинной нитью, равномерно заряженной с линейной плотностью t=30 нКл/м. На расстоянии а =20 см от нити находится плоская круглая площадка радиусом r =1 см. Определить поток вектора напряженности через эту площадку, если плоскость ее составляет угол b=30° с линией напряженности, проходящей через середину площадки.

Решение. Поле, создаваемое бесконечно равномерно, заряженной нитью, является неоднородным. Поток вектора напряженности в этом случае выражается интегралом

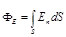, (1)

где E_n — проекция вектора Е на нормаль n к поверхности площадки dS. Интегрирование выполняется по всей поверхности площадки, которую пронизывают линии напряженности.

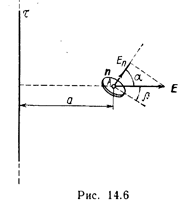Проекция Е_п вектора напряженности равна, как видно из рис. 14.6,

Е_п=Е cosa,

где a — угол между направлением вектора и нормалью n. С учетом этого формула (1) примет вид

.

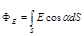Так как размеры поверхности площадки малы по сравнению с расстоянием до нити (r<<a), то электрическое поле в пределах площадки можно считать практически однородными. Следовательно, вектор напряженности Е очень мало. меняется по модулю и направлению в пределах площадки, что позволяет заменить под знаком интеграла значения Е и cosa их средними значениями < E > и <cosa> и вынести их за знак интеграла:

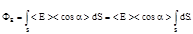
Выполняя интегрирование и заменяя < E > и <cosa> их приближенными значениями Е_A и cos a_A, вычисленными для средней точки площадки, получим

Ф _E = Е_A cos a_AS =p r ² Е_A cosa _A. (2)

Напряженность Е_A вычисляется по формуле E_A =t/(2pe ₀a). Из

рис. 14.6 следует cos a_A =cos(p/2 —b)=sinb.

С учетом выражения Е_A и cos a_A равенство (2.) примет вид

.

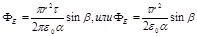Подставив в последнюю формулу данные и произведя вычисления, найдем

Ф _E =424 мВ.м.

Пример 7. Две концентрические проводящие сферы радиусами R₁ =6 см и R₂= 10 см несут соответственно заряды Q₁ =l нКл и Q₂ = –0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r₁ =5 см, r₂ =9 см r₃ =15см. Построить график Е(r).

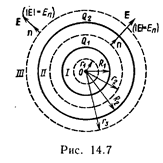Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 14.7): область I (r < R₁), область II (R₁ < r₂ < R₂), область III (r₃ > R₂).

1. Для определения напряженности E₁ в области I проведем сферическую поверхность S₁ радиусом r₁ и воспользуемся теоремой Остроградского—Гаусса. Так как внутри области I зарядов нет, то согласно указанной теореме получим равенство

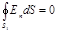, (1)

где E_n — нормальная составляющая напряженности электрического поля.

Из соображений симметрии нормальная составляющая E_n должна быть равна самой напряженности и постоянна для всех точек сферы, т. е. En=E₁= const. Поэтому ее можно вынести за знак интеграла. Равенство (1) примет вид

.

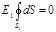Так как площадь сферы не равна нулю, то

E₁ =0,

т. е. напряженность поля во всех точках, удовлетворяющих условию r₁<.R₁, будет равна нулю.

2. В области II сферическую поверхность проведем радиусом r₂. Так как внутри этой поверхности находится, заряд Q₁,тодля нее, согласно теореме Остроградского—Гаусса,можно записать равенство

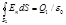. (2)

Так как E_n = E₂ =const, то из условий симметрии следует

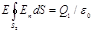, или ES₂ = Q₁ /e ₀,

откуда

E₂ = Q₁ /(e ₀ S ₂).

Подставив сюда выражение площади сферы, получим

E₂ = Q /(4 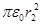). (3)

3. В области III сферическую поверхность проведем радиусом r₃. Эта поверхность охватывает суммарный заряд Q₁ + Q₂. Следовательно, для нее уравнение, записанное на основетеоремыОстроградского — Гаусса, будет иметь вид

.

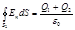Отсюда, использовав положения, примененные в первых двух случаях, найдем

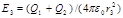. (4)

Убедимся в том, что правые части равенств (3) и (4) дают единицу напряженности электрического поля;

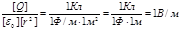
Выразим все величины в единицах СИ (Q₁ =10^-9 Кл, Q₂ = –0,5´10^-9 Кл, r₁ =0,09 м, r₂ =15м, l/(4pe ₀)=9×10⁹ м/Ф) и произведем вычисления:

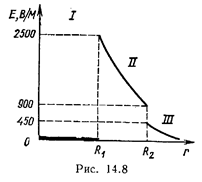
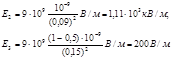
4. Построим график E (r). В области I (r₁<R₁) напряженность E =0. В области II (R₁ 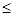r<.R₂) напряженность E₂ (r) изменяется по закону l/r ². В точке r=R₁ напряженность E₂ (R₁)=Q ₁ /(4pe ₀R 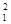)=2500 В/м.В точке r=R₁ (r стремится к R₁ слева) E₂(R₂)=Q₁ /(4pe ₀R 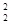)=900В/м. В области III (r > R₂) E₃ (r) изменяется по закону 1/ r², причем в точке r=R₂ (r стремится к R₂ справа) Е₃(R₂) =(Q₁–|Q₂ |)/(4pe ₀R 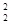)=450 В/м. Таким образом, функция Е (r) в точках r = R₁ и r=R₂ терпит разрыв. График зависимости Е(r) представлен на рис. 14.8.

Дата добавления: 2015-05-06