Сведения, необходимые для выполнения работы. Целью работы является:

ЦЕЛЬ РАБОТЫ

ИССЛЕДОВАНИЕ ВОЛЬТАМПЕРНОЙ ХАРАКТЕРИСТИКИ ТУННЕЛЬНОГО ДИОДА

Целью работы является:

• получение вольтамперной характеристики (ВАХ) туннельного дио­да;

• построение полиномиальной модели ВАХ туннельного диода;

• определение электрических параметров туннельного диода.

Перед началом работы полезно ознакомиться со следующими вопро­сами:

• особенности устройства и работы туннельного диода [1, с. 36-39],

• вид ВАХ туннельного диода [1, с. 37-38],

• способы построения полиномиальных регрессионных моделей [6, с. 26-32],

Для того чтобы охарактеризовать свойства ТД используют ряд ха-

• способы проверки качества регрессионных моделей [6, с. 38-50].
Туннельный диод представляет собой p-n-переход, характеризую­
щийся высоким содержанием примесей как в р-зоне, так и в n-зоне. Высо­
кая концентрация примесей вызывает появление у ТД особых свойств,
проявляющихся как участок с отрицательным сопротивлением на ВАХ ТД.
Этот участок хорошо виден (от точки 1 и до точки 2) на типовой ВАХ ТД,
изображенной на рис.3.1.

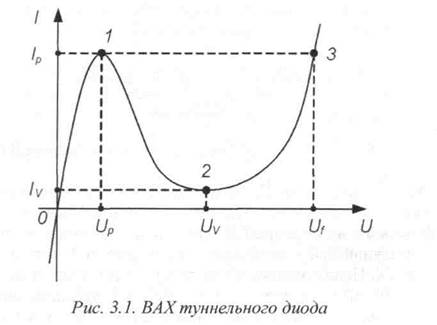
рактеристик по постоянному току. Важнейшими среди них являются: пи­ковое напряжение (U_p), пиковый ток (I_р), напряжение впадины (U_v), ток впадины (/„), безразмерный параметр B=Ip/I_v (отношение пикового тока к току впадины) и напряжение, при котором ток на стандартном участке ха­рактеристики совпадает с пиковым током (Uj).

Эти характеристики зависят от материала, из которого изготовлен диод (табл.3.1).

Для получения ВАХ используется электрическая схема подключения ТД, изображенная на рис.3.2. Напряжение, изменяющееся по линейному зако­ну в диапазоне примерно от -0,15В до +1,4В, подается с выхода ВП на иссле­дуемую схему, при этом с помощью того же ВП измеряется падение напряже­ния на измерительном сопротивлении и р-n переходе ТД. Далее полученные данные представляются на графическом индикаторе ВП и обрабатываются.

Падение напряжения U_R на измерительном сопротивлении R прямо пропорционально току через ТД, поэтому, откладывая по вертикальной оси графического индикатора ВП напряжение пропорциональное Ur/R, a по горизонтальной оси - напряжение U_R можно получить на экране изо­бражение ВАХ. Используемый в работе ВП имеет порог чувствительности примерно 0,003 мВ (этот порог определяется характеристиками платы вво­да-вывода PCI-6251), в связи с этим необходимо выбрать R таким образом, чтобы при протекании через диод пикового тока напряжение на измери-

тельном сопротивлении составляло примерно 1 мВ. На лабораторном стенде установлен AsGa ТД, для которого пиковый ток колеблется в диа­пазоне от 1 мА до 10 мА, поэтому R выбран равным 1 Ом.

Для того, чтобы вычислить электрические характеристики ТД по по­стоянному току можно использовать математическую модель ВАХ, а так­же графическое или табличное представления ВАХ.

Для определения математической зависимости между током и на­пряжением необходимо в прямоугольной системе координат получить на­бор отсчетов (X1,y1), {х₂,у2\ • • •» (хn,уn). Для получения этого набора в лабо­раторной работе используется LabVIEW BП. Если провести через полу­ченные точки плавную кривую можно наглядно увидеть ВАХ. Существен­ным вопросом является нахождение такой кривой, которая наилучшим способом отвечает полученным данным. Поскольку в эксперименте можно произвольно изменять напряжение U_D, то оно будет являться независимой переменной (х). Соответственно ток I_D является зависимой переменной (у). Для широкого круга задач нахождение математической зависимости, и, со­ответственно, наилучшей кривой, описывающей экспериментальные дан­ные, заключается в нахождении подходящего полинома степени к:

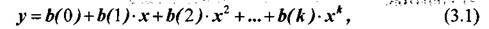
где b(j) постоянные коэффициенты.

Применительно к рассматриваемой задаче это уравнение принято на­зывать полиномиальной регрессией, а коэффициенты b(j) - коэффициен­тами регрессии.

Для нахождения коэффициентов регрессии в лабораторной работе ис­пользуется специальная процедура, осуществляемая в среде LabVIEW. Рас­четы начинают для модели, которая обладает самой простой структурой и, по мнению экспериментатора, может обеспечить согласие между значениями зависимой переменной y(i), измеренными в эксперименте, и вычисленными по уравнению регрессии значениями h(i). Для оценки качества модели ис­пользуется специальная статистическая процедура, называемая проверкой адекватности модели. Модель адекватна, если оценка дисперсии относи­тельно регрессии SS(ocm), и независимая от нее оценка дисперсии случайных возмущений SS(e), оказывающих влияние на результаты измерений отклика, статистически неотличимы друг от друга. Оценка значения SS(ocm) прово­дится при построении регрессионной модели по формуле:

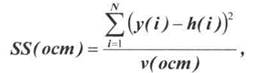
(3.2)

где N- общее число наблюдений;

v(ocm) = N -k- 1 - число степеней свободы остаточной суммы

квадратов.

уф - результату -ого наблюдения;

h(j) — значение отклика, вычисленное по уравнению регрессии. Оценка значения SS(e) проводится по результатам специальной се­рии независимых наблюдений по формуле:

где уф - результату -ого наблюдения;

(3.3)

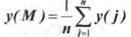
- среднее значение результатов наблюдений;

п - оощее число независимых наблюдении. Эта серия наблюдений выполняется при неизменных условиях и при фик­сированном значении независимой переменной х, поэтому на результатах измерения уф сказывается только влияние случайных возмущений. При выполнении серии независимых наблюдений количество опытов п и зна­чение переменной х: выбирает экспериментатор. Если закон распределения величины уф предполагается нормальным, то достаточно, как правило, 10 -15 опытов.

Собственно процедура проверки адекватности заключается в вычис­лении дисперсионного отношения F=SS(ocm)/SS(e) и сравнении полученно­го результата с табличным значением F, функции распределения Фишера.

Величина F имеет распределение Фишера с v(ocm) = N-k-1 и v(e) = п-1 степенями свободы. Для заданного уровня значимости а по таблице распределения Фишера с v(ocm) и v(e) степенями свободы находят величи­ну Fi=F(a,v(ocm), v(e)). Если F< F_t, то гипотеза о статистическом равенст-ве S_ocm и SS(e) не отвергается и модель признается адекватной, если F> F_t модель считается неадекватной.

Данная процедура может быть реализована, если SS(ocm)>SS(e), в противном случае вычисляется обратное дисперсионное соотношение:

(3.4)

а для нахождения F_t пользуются таблицей распределения Фишера с v(e) = п-1 и v(ocm) — N-k-1 степенями свободы. Выводы, которые при этом де­лаются, аналогичны предыдущим.

Как правило, при выполнении экспериментальных исследований в технике уровень значимости а принимается равным 0,05.

Если первоначально выбранная модель окажется неадекватной, структуру модели усложняют, повышая степень полинома на единицу. Данные обрабатывают снова, получают новые оценки коэффициентов рег­рессии и вновь проверяют гипотезу об адекватности. Эта процедура вы­полняется до тех пор, пока не получится удовлетворительное согласование экспериментальных данных и результатов расчетов по модели.

Для получения координат локальных экстремумов (точки 1 и 2, рис.3.1) адекватную модель анализируют стандартными математическими методами. Значение ЩЗ) находят из уравнения:

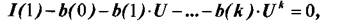
(3.5)

которое в заданном диапазоне изменения величины U имеет 2 действи­тельных корня (точки 1 и 3, рис.3.1). Эти операции удобно выполнять на компьютере с помощью одного из стандартных пакетов для математиче­ской обработки данных.

Дата добавления: 2015-05-06