
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Программа работы и порядок ее выполнения
|
|
|
|
Или.
Логика срабатывания операции «И-НЕ» заключается в том, что сигнал на выходе этого ЛЭ будет в том случае, если отсутствует сигнал хотя бы на одном входе. Эта операция известна также под названием «штрих Шеффера», образует сложное высказывание из простых по следующему правилу: сложное высказывание истинно, если ложно хотя бы одно из простых высказываний, и ложно, если все простые высказывания истинны (см. таблицу 10.1).
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим «2И-НЕ», если три сигнала, то «3И-НЕ», или символьно:
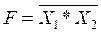 ,
,  соответственно и так далее.
соответственно и так далее.
5. Отрицание логического сложения, или операция «ИЛИ-НЕ». Графическое обозначение операции — рисунок 10.2, б. Символически операция записывается выражениями:
 или
или 
Смысл этой операции состоит в том, что на выходе этого устройства сигнал будет лишь в том случае, если нет сигналов на его входах. Если появится сигнал хотя бы на одном входе ЛЭ, реализующего операцию «ИЛИ-НЕ», то на выходе сигнала не будет. Операция «ИЛИ-НЕ» называется также «стрелкой Пирса», образует сложное высказывание из простых в соответствии со следующим правилом: сложное высказывание истинно лишь в том случае, когда ложны все образующие его простые высказывания, и ложно, если истинно хотя бы одно из простых высказываний (см. таблицу 10.1).
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим: «2ИЛИ-НЕ», если три сигнала, то «3ИЛИ-НЕ», или символьно
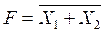 ,
,  соответственно и так далее.
соответственно и так далее.

| 
|
| а) | б) |
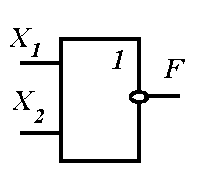
Рисунок 10.2 — Графические обозначения составных логических элементов (операций):
а — элемент «И-НЕ»; б — элемент «ИЛИ-НЕ»
Таблица 10.1
| X 1 | X 2 | F | |||
| «И» | «ИЛИ» | «2И-НЕ» | «2ИЛИ-НЕ» | ||
В зависимости от вида используемых сигналов ЛЭ подразделяют на потенциальные, в которых «0» (false) или «1» (true) задаются двумя различными уровнями постоянного напряжения. Низкий уровень напряжения соответствует «0», высокий — «1». Также ЛЭ бывают импульсными, в которых «0» означает отсутствие импульса, а «1» соответствует наличию импульса. Наибольшее распространение получили потенциальные ЛЭ.
ЛЭ выполняются чаще всего на основе интегральных микросхем (ИМС) определенной серии, например К155.
В данной лабораторной работе исследуются логические элементы
«2И-НЕ» (К155ЛАЗ) и «2ИЛИ-НЕ» ( К155ЛЕI), условные обозначения которых показаны на рисунке 10.2, а и б соответственно.
На основе этих базовых ЛЭ могут быть созданы комбинационные логические устройства, выполняющие операции любой сложности. В комбинационных устройствах сигнал на выходе F определяется комбинацией входных сигналов Х 1, Х 2, Х 3, ….
Пусть требуется создать комбинационную схему с тремя входами Х 1, Х 2, Х 3 и одним выходом F. Высокий уровень напряжения на выходе должен появляться только при высоких уровнях на входах Х 1 и Х 2, т.е. F = 1 при Х 1 = Х 2 = 1 и Х 3 = 0.
Любую комбинационную схему можно составить путем подбора элементов. В данном случае, если использовать ЛЭ с двумя входами, а именно «2И-НЕ» и «2ИЛИ-НЕ», то она будет содержать не менее четырех входов. Три входа необходимы для входных величин Х 1, Х 2, Х 3 и один вход можно использовать для связи между ЛЭ.
Так как схема должна реагировать на появление одинаковых высоких уровней (или импульсов) Х 1 и Х 2, то эти входы следует объединить ЛЭ «2И-НЕ». На его выходе получим низкий уровень при наличии Х 1 = Х 2 = 1.
Следовательно, второй ЛЭ должен давать на выходе высокий потенциал F = 1 только при поступлении на его входы двух низких уровней, т.е. при отсутствии сигналов на его двух входах. Поэтому таким вторым элементом схемы является ЛЭ «2ИЛИ-НЕ» (рисунок 10.3).

Рисунок 10.3 — Простейшее комбинационное устройство на основе логических элементов
При большом числе входов такой метод подбора трудоёмок. Более рационально составление уравнения логической функции и последующая ее декомпозиция и оптимизация по правилам булевой алгебры, или алгебры логики. Для данного случая представление операции выразится формулой:
 .
.
Чтобы разобраться, какие ЛЭ здесь необходимо взять, надо его
преобразовать, используя тождество 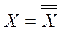 . Оно означает, что двойное «НЕ» может означать «ДА». Кроме того, здесь надо применить формулы Моргана:
. Оно означает, что двойное «НЕ» может означать «ДА». Кроме того, здесь надо применить формулы Моргана:
 и
и 
Смысл первой формулы заключается в том, что если отсутствуют первый Х 1 и второй Х 2 сигналы (операция логического умножения отсутствующих сигналов), то операция переходит в логическое «2ИЛИ-НЕ», т.е. на выходе отсутствует сигнал, так как нет Х 1 или Х 2 (по сути дела, их нет обоих).
Смысл второй формулы состоит в том, что если нет сигнала Х 1 или Х 2 (операция логического сложения отсутствующих сигналов), то операция переходит в «2И-НЕ», т.е. на выходе нет сигнала, так как нет Х 1 и нет Х 2.
Исходя из этого, формулу рассматриваемой операции можно преобразовать следующим образом:
 ,
,
где  — введенное обозначение.
— введенное обозначение.
Полученное выражение показывает, что, во-первых, нужен ЛЭ
«2ИЛИ-НЕ», чтобы выполнить операцию  , во-вторых, нужен ЛЭ
, во-вторых, нужен ЛЭ
«2И-НЕ», осуществляющий операцию в соответствии с  .
.
Многие комбинационные устройства, встречающиеся в цифровой вычислительной технике (шифраторы, дешифраторы, сумматоры), представляют собой готовые ИМС. В данной работе используется четырехразрядный сумматор, выполненный на микросхеме К155ИМЗ, структурная схема которого показана на рисунке 10.4. Состоит он из четырех одноразрядных сумматоров SМ. Каждый одноразрядный сумматор имеет три входа: два входа А и В для ввода двух суммируемых чисел одного разряда и вход Р -перенос, на который поступает сигнал с выхода предыдущего разряда как результат сложения в нем чисел. На выходе S появляется сигнал, соответствующей сумме двух чисел двоичного кода, а на выходе Р — сигнал переноса, если в результате сложения получается двухзначное число. Например, необходимо сложить два двоичных четырехразрядных числа — А = 0101 (десятичное число 5) и В = 1001 (9). На входы сумматора поступят А 0 = 1 и В 0 = 1, в результате получится в двоичном коде 1 + 1 = 10 (в десятичном коде 2). Поэтому на выходе S 0 =0, а Р = 1. На входы второго сумматора поступят А 1 = 0, В 1 = 0, Р = 1. На выходе получится единица в этом разряде S 1 = 1 и Р = 0, т.е. в следующий разряд нуль переносится. На третьем сумматоре А 2 = 1, В 2 = 0 и Р = 0. В результате получится S 2 = 1, Р = 0 (см. таблицу 10.2).

Рисунок 10.3 — Схема четырехбитного сумматора
Таблица 10.2
| Числа | Двоичный код | Десятичный код |
| A | 0 1 0 1 | |
| B | 1 0 0 1 | |
| A+B | 1 1 1 0 |
Сумматор с большим числом разрядов объединяет несколько простых.
1. Исследовать ЛЭ «2И-НЕ», для чего на входы Х 1 и Х 2 поочередно подать напряжения логической единицы и нуля от источников через переключатели SА 1… SА 8. Для индикации уровня выходного напряжения выход элемента F соединить с одним из индикаторов МL 1… ML 5. Составить и заполнить таблицу истинности (таблица10.3).
2. Исследовать ЛЭ «2ИЛИ-НЕ» аналогичным образом. Результаты также записать в таблицу 10.3.
Таблица 10.3
| Х 1 | Х 2 | 
| 
| 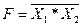
|
3. Собрать на стенде электрическую схему описанного в пособии комбинационного устройства (рисунок 10.3), обеспечивающего выходной сигнал F = 1 только при наличии двух входных сигналов Х 1 = Х 2 = 1, если третий сигнал входной Х 3 = 0. Проверить ее работу, подав на входы Х 1, Х 2, Х 3 входные сигналы, и включить на выход индикатор F. Перебрать все возможные комбинации входных сигналов и результаты свести в таблицу 10.4.
Таблица 10.4
| X 1 | X 2 | X 3 | F | X 1 | X 2 | X 3 | F |
4. Собрать на стенде электрическую схему четырехразрядного сумматора, собранного на одной микросхеме типа К155ИМ3, для чего на входы А 0… А 3 и В 0… В 3 подать сигнал от источника через ПК SA 1… SA 8, а вход CR подключить к “земле” ( ). С выходов сумматора S 0, S 1, S 2, S 3 и СRР подать сигналы на индикаторы МL1 … МL 5.
). С выходов сумматора S 0, S 1, S 2, S 3 и СRР подать сигналы на индикаторы МL1 … МL 5.
Каждому студенту бригады необходимо взять два четырехразрядных числа (см. таблицу 10.5) в двоичной системе (в десятичной системе это означает, что числа должны быть не больше 15) и осуществить их суммирование.
Таблица 10.5
Соответствие четырехразрядных двоичных чисел десятичным числам
| Двоичный код | Десятичное число | Двоичный код | Десятичное число | Двоичный код | Десятичное число |
| 0 0 0 0 | 0 1 1 0 | 1 0 1 1 | |||
| 0 0 0 1 | 0 1 1 1 | 1 1 0 0 | |||
| 0 0 1 0 | 1 0 0 0 | 1 1 0 1 | |||
| 0 0 1 1 | 1 0 0 1 | 1 1 1 0 | |||
| 0 1 0 0 | 1 0 1 0 | 1 1 1 1 | |||
| 0 1 0 1 | 1 0 0 0 0 |
Полученные результаты всей бригады записать в таблицу 10.6
Таблица 10.6
| Числа | Десятичный код | Двоичный код | Числа | Десятичный код | Двоичный код |
| А | А | ||||
| В | В | ||||
| А+В | А+В |
Содержание отчета
1. Название и цель работы.
2. Программа работы и порядок ее выполнения, включая схемы и формулы.
3. Результаты экспериментального исследования в виде таблиц.
4. Осцилограммы напряжения для исследуемых типов выпрямителей.
4. Сравнительная оценка полученных результатов и выводы.
ЛИТЕРАТУРА
1. Касаткин, А.С. Электротехника / А.С. Касаткин, М.В. Немцов. — Москва: Энергоатомиздат, 1983.— 427 с.
2. Посудевский, А.А. Электропитание радиоэлектронных средств / А.А. Посудевский. — Москва: Воениздат, 1980. — 248 с.
3. Кiтуновiч, Ф.Г. Электратэхнiка / Ф.Г. Кiтуновiч. — Мiнск: Вышэйшая школа, 1998. — 429 с.
4. Автомобиль. Основы конструкции / Н.Н. Вишняков [и др.]. — Москва: Машиностроение, 1986.
5. Электротехника / Б.А. Волынский, В.Н. Зейн, В.Е. Шатерников. — Москва: Энергоатомиздат, 1987.
6. Асинхронные машины / под ред. И.П. Копылова. — Москва: Высшая школа, 1977. 328 с.
7. Осин, И.Л. Электрические машины. Синхронные машины / И.Л. Осин, Ю.Г. Шакарян; под ред. И.П. Копылова. — Москва: Высшая школа, 1990. 304 с.
8. Хвостов, В.С. Электрические машины. Машины постоянного тока / В.С. Хвостов; под ред. И.П. Копылова. — Москва: Высшая школа, 1989. — 335 с.
9. Морозов, А.Г. Электротехника, электроника и импульсная техника / А.Г. Морозов. — Москва: Высшая школа, 1987.
10. Галкин, В.И. Промышленная электроника / В.И. Галкин. — Минск: Вышэйшая школа, 1989.
11. Лабораторные работы (практикум) по курсу «Электротехника и электроника» для студентов неэлектрических специальностей: Ч. 3. Электроника / Розум Т.Т. [и др.]. — Минск: БГПА, 1988.
ПРИЛОЖЕНИЯ
Приложение 1
Основные условные обозначения измерительных механизмов приборов
| Наименование системы и преобразователя | Условное обозначение |
| Обычный измери-тельный механизм | Логометрический измери-тельный механизм |
| Магнитоэлектрический прибор с подвижной рамкой Магнитоэлектрический прибор с подвижным магнитом Электромагнитный прибор Электромагнитный поляризованный прибор Электродинамический прибор Ферродинамический прибор Индукционный прибор Электростатический прибор Тепловой прибор (с нагреваемой проволокой) |

|
Приложение 2
Условные обозначения особенностей работы
электроизмерительных приборов
| Значение данного обозначения | Условное обозначение |
| Приборы предназначаются для работы в цепи только постоянного тока | 
|
| Приборы предназначаются для работы в цепи постоянного и переменного токов | 
|
| Приборы предназначаются для работы в цепи только однофазного переменного тока | 
|
| Приборы предназначаются для работы в цепи трехфазного тока | 
|
| Прибор нормально работает: | |
| при вертикальном положении шкалы | 
|
| при горизонтальном положении шкалы | 
|
| при наклонном положении шкалы | 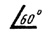
|
| Измерительная цепь изолирована от корпуса и испытана напряжением, например 2 кВ | 
|
| Прибор испытанию изоляции не подлежит | 
|
| Защита от внешних магнитных полей | 
|
| Защита от внешних электрических полей | 
|
| Внимание! См. дополнительные указания в паспорте и инструкциям по эксплуатации | 
|
| Осторожно! Прочность изоляции измерительной цепи по отношению к корпусу не соответствует нормам (знак выполнен красным) | 
|
Приложение 3
Буквенные обозначения и единицы основных величин в электротехнике
| Величина | Обозначения | Единицы | ||
| Наименование | главные | запасные | наименование | обозначение |
| Время | t | — | секунда | C |
| Ёмкость электрическая | C | — | фарада | Ф |
| Заряд электрический | Q | — | кулон | Кл |
| Индуктивность | L | — | генри | Гн |
| Индуктивность взаимная | M | Lmn | генри | Гн |
| Индукция магнитная | B | — | тесла | Тл |
| Коэффициент мощности при синусоидальном напряжении и токе | сos j | — | — | — |
| КПД | h | — | — | — |
| Коэффициент трансформации | n | — | — | — |
| Коэффициент трансформации трансформатора напряжения | к | к U | ||
| Коэффициент трансформации трансформатора тока | к | кт | ||
| Мощность активная | P | — | ватт | Вт |
| Мощность реактивная | Q | Pa | вольт-ампер реактивный | ВАр |
| Мощность полная | S | P S | вольт-ампер | ВА |
| Напряжение электрическое | U | — | вольт | В |
| Напряженность магнитного поля | H | — | ампер на метр | А/м |
| Период колебаний электрической или магнитной величины | T | — | секунда | с |
| Постоянная магнитная | m0 | — | генри на метр | Гн/м |
| Постоянная электрическая | e0 | — | фарада на метр | Ф/м |
Продолжение приложения 3
| Величина | Обозначения | Единицы | ||
| Наименование | главные | запасные | наименование | обозначение |
| Потенциал электрический | φ | — | вольт | В |
| Поток магнитный | Ф | — | вебер | Вб |
| Потокосцепление | Y | — | вебер | Вб |
| Проводимость электрическая активная | G | g | сименс | См |
| Проводимость электрическая полная | Y | y | сименс | См |
| Проводимость реактивная | B | в | сименс | См |
| Проницаемость диэлектрическая абсолютная | e a | e | фарада на метр | Ф/м |
| Проницаемость диэлектрическая относительная | e r | — | ||
| Проницаемость магнитная абсолютная | m а | m | генри на метр | Гн/м |
| Проницаемость магнитная относительная | m r | — | — | — |
| Плотность тока | J | — | ампер на квадратный метр | А/м2 |
| Разность электрических потенциалов | U | — | вольт | В |
| Сдвиг фаз между напряжением и током | j | — | градус | ° |
| Сила электродвижущая (ЭДС) | E | — | вольт | В |
| Скольжение | s | — | — | — |
Окончание приложения 3
| Величина | Обозначения | Единицы | ||
| Наименование | главные | запасные | наименование | обозначение |
| Сопротивление электрическое постоянному току | R | r | ом | Ом |
| Сопротивление электрическое активное | R | r | ом | Ом |
| Сопротивление электрическое полное | Z | — | ом | Ом |
| Сопротивление электрическое реактивное | X | x | ом | Ом |
| Ток | I | — | ампер | А |
Приложение 4
Обозначения условные графические и буквенные в электрических схемах
| Наименование | Графическое обозначение | Буквенное обозначение |
| Постоянный ток | — | |
| Полярность постоянного тока положительная | + | |
| Полярность постоянного тока отрицательная | — | |
| Переменный ток | ~ | |
| Переменный ток частотой 50 Гц | ~50 Гц | |
| Трехфазный ток частотой 50 Гц, напряжением 220 В | 3 N ~50Гц 220В | |
| Трехфазный ток, четырехпроводная линия (три провода, нейтраль) частотой 50 Гц, напряжением 220/380 В | 3 N ~50Гц 220/380 В | |
| Резистор постоянный | 
| R |
| Резистор постоянный с дополнительными отводами | 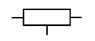
| R |
| Шунт измерительный | 
| R |
| Резистор переменный | 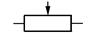
| R |
| Терморезистор | 
| RK |
| Варистор | 
| RU |
| Потенциометр | 
| R |
| Конденсатор постоянной ёмкости | 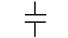
| C |
| Конденсатор постоянной ёмкости электролитический | 
| C |
| Конденсатор переменной ёмкости | 
| C |
Продолжение приложения 4
| Наименование | Графическое обозначение | Буквенное обозначение |
| Вариконд | 
| C |
| Катушка индуктивности | 
| L |
| Дроссель с ферромагнитным магнитопроводом | 
| L |
| Трансформатор однофазный двухобмоточный с ферромагнитным сердечником | 
| TV |
| Автотрансформатор с ферромагнитным сердечником | 
| TV |
| Измерительный трансформатор тока | 
| TA |
| Трансформатор трехфазный с ферромагнитным магнитопроводом двухобмоточный с соединением обмоток «звезда»–«звезда» с выведенной нейтральной точкой | 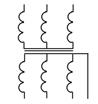
| TV |
| Генератор постоянного тока со смешанным возбуждением | 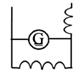
| G |
| Синхронный генератор трехфазный с обмотками, соединенными в звезду, с невыведенной нейтралью | 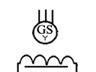
| G |
| Двигатель постоянного тока с параллельным возбуждением | 
| M |
| Асинхронный двигатель трехфазный, соединенный в треугольник, с короткозамкнутым ротором | 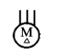
| M |
| Амперметр | 
| PA |
| Вольтметр | 
| PV |
Окончание приложения 4
| Наименование | Графическое обозначение | Буквенное обозначение |
| Ваттметр | 
| PW |
| Счетчик активной энергии | 
| PI |
| Частотомер | 
| PF |
| Фазометр | 
| |
| Омметр | 
| PR |
| Гальванометр | 
| |
| Осциллограф | 
| |
| Контакт замыкающий коммутационного устройства | 
| QS |
| Контакт размыкающий коммутационного устройства | 
| QS |
| Контакт переключающий с нейтральным центральным положением | 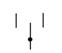
| SA |
| Разъединитель трехполюсный | 
| QS |
| Контакт выключателя замыкающий трехполюсный с автоматическим срабатыванием максимального тока | 
| QF |
| Переключатель однополюсный шестипозиционный | 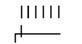
| SA |
| Предохранитель плавкий | 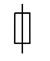
| FU |
Приложение 5
Основные формулы и уравнения электротехники
| Мощность | p = ui |
| Энергия | W = 
|
| Энергия магнитного поля катушки | W маг = 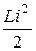
|
| Энергия электрического поля конденсатора | W эл = 
|
Связи электрических величин (причины и следствия)

| Закон Ома | i = 
|
| Закон Джоуля–Ленца | 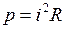
|
| Закон электромагнитной индукции | e = 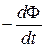
|
| Закон Ампера | 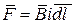
|
| Закон полного тока | 
|
Соотношения между током и напряжением на элементах электрической цепи
| Элемент цепи | Вид тока | |||
| Переменный ток, мгновенное значение | Синусоидальный ток, комплексное значение | Синусоидальный ток, действующее значение | Постоянный ток | |
| R | u = iR
i = 
| 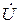 = =  R R
 = = 
| U = IR
I = 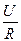
| U = IR
I = 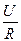
|
| L | uL= L 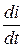 i=
i= 
| 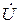 = j w L = j w L 
 = = 
| U = w LI
I = 
| Индуктивность не оказывает сопротивления постоянному току |
| C | uC =  i = С
i = С 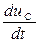
| 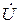 = = 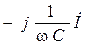
 = j ω C = j ω C 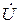
| U =  I = w CU
I = w CU
| Ёмкость представляет собой разрыв цепи для постоянного тока |
Закон Ома
в комплексной форме для цепи синусоидального тока:
 = =  ; ;  = =  . .
|
Учебное издание
Редактор Н.Ф. Крицкая
Компьютерная верстка Н.Ф. Крицкая
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 717; Нарушение авторских прав?; Мы поможем в написании вашей работы!