
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сведения из теории. 1. Изучить принцип построения логических элементов цифровых интегральных микросхем;
|
|
|
|
Подготовка к работе
ИЗУЧЕНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ И КОМБИНАЦИОННЫХ УСТРОЙСТВ
ЛАБОРАТОРНАЯ РАБОТА № 10
Цель работы:
1. Изучить принцип построения логических элементов цифровых интегральных микросхем;
2. Изучить принцип построения комбинационных устройств на основе логических элементов;
3. Экспериментально исследовать логические элементы и комбинационные устройства.
1. Изучить тему «Логические элементы и комбинационные устройства» по конспекту лекций и по [3, § 10.1, 10.3].
2. Ознакомиться с описанием лабораторной работы по методическим указаниям.
3. Самоконтроль:
1) Назначение и области применения логических элементов (ЛЭ);
2) Основные логические операции и их реализация;
3) Что представляют собою потенциальные и импульсные ЛЭ;
4) Назначение и работа ЛЭ «И-НЕ», «ИЛИ-НЕ».
5) Что такое комбинационные устройства?
6) Схема и работа комбинационных устройств при различных входных сигналах;
7) Что такое сумматор?
8) Работа и схема четырехразрядного сумматора.
4. Оформить протокол для отчета.
В ЭВМ, цифровых измерительных приборах и других цифровых устройствах широко применяются логические элементы (ЛЭ). Каждый ЛЭ выполняет вполне определенную логическую операцию над цифровой информацией. ЛЭ создают на базе электронных устройств, работающих в ключевом режиме. Ключевой режим характеризуется двумя состояниями ключа: включено — отключено. Поэтому любую информацию необходимо преобразовать в цифровой двоичный код, при котором цифра каждого разряда принимает только два значения: 0 (логический нуль) и 1 (логическая единица). Это соответствует двум состояниям ключа.
Для описания логических операций используется математический аппарат, получивший название алгебры логики, или булевой алгебры в честь его создателя — ирландского ученого Джорджа Буля. Алгебра логики изучает взаимосвязь между простыми высказываниями, образующими сложные высказывания. Исходя из булевой алгебры простое высказывание может иметь только два значения — истинное (true) или ложное (false). Одно из этих значений принимается за единицу, второе — за нуль. Уровень выходного напряжения ЛЭ зависит от уровня входного (или нескольких входных) напряжения. Эта связь отображается формулой и таблицей состояний, или таблицей истинности.
Логические операции преобразуют по определенным правилам входную информацию, обозначаемую символами Х 1, Х 2, Х 3, ..., Хn, в выходную, которую обозначим буквой F. Условные обозначения основных логических элементов показаны на рисунке 10.1, таблица истинности приведена в таблице 10.1 для двух значений входных сигналов — Х 1 и Х 2.
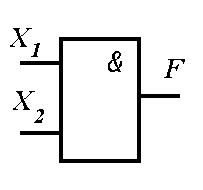
| 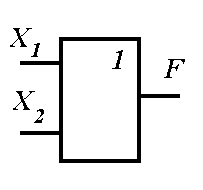
| 
|
| а) | б) | в) |
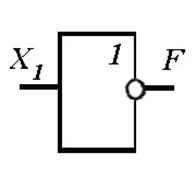
Рисунок 10.1 — Графические обозначения основных логических элементов (операций):
а — элемент «И», б — элемент «ИЛИ», в — элемент «НЕ»
Рассмотрим основные логические операции.
1. Логическое умножение (конъюнкция), или операция «И», обозначается в формулах булевой алгебры знаками «*» или «^». Символически операция записывается выражениями:
F = Х 1 * Х 2 * Х 3 * … * Хn или F = Х 1 ^ Х 2 ^ Х 3 ^… ^ Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ будет сигнал «1» только в том случае, если на и X 1,и Х 2,и Х 3, и т.д.входы поступят, т.е. если на входах будут все сигналы, предусмотренные в данной операции (все true), то и на выходе будет сигнал (truе). При этом ложное высказывание будет истинным, если истинны все простые высказывания.
Графическое обозначение операции — рисунок 10.1, а.
2. Логическое сложение (дизъюнкция), она же операция «ИЛИ», обозначается знаками «+», «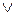 ». Символически операция записывается следующими выражениями:
». Символически операция записывается следующими выражениями:
F = Х 1 + Х 2 + Х 3 + … + Хn; F = Х 1 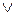 Х2
Х2 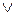 Х 3
Х 3 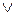 …
… 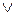 Хn.
Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ «ИЛИ» будет сигнал «1» в том случае, если на его входы или Х 1, или Х 2, или Х 3 и т.д. поступит хотя бы один сигнал «1» из всех предусмотренных. Другими словами, сложное высказывание будет истинным (truе), если истинно хотя бы одно из простых высказываний, и ложным (false), если ложны (false) все простые высказывания. Графическое обозначение операции — рисунок 10.1, б.
3. Логическое отрицание (инверсия), или «НЕ», обозначается чертой над входной (входными) переменной. Символически записывается:
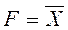 .
.
На схемах условное обозначение этой логической операции — кружочек на выходе прямоугольника (рисунок 10.1, в). Смысл этой операции состоит в том, что на выходе этого ЛЭ сигнал будет лишь в том случае, если на входе сигнала нет. Если на входе есть сигнал, то на выходе он отсутствует. Это простое отрицание, которое используется сравнительно редко.
Гораздо чаще используется операция «НЕ» в сочетании с операциями «И» или «ИЛИ». Рассмотрим такие составные операции.
4. Отрицание логического умножения, или операция «И-НЕ». Графическое обозначение операции — рисунок 10.2, а. Символически операция записывается выражениями:
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 613; Нарушение авторских прав?; Мы поможем в написании вашей работы!