
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример расчёта цепи переменного тока со смешанным соединением электроприёмников методом проводимостей и полного сопротивления
|
|
|
|
Часть 2. Электрические цепи переменного тока
2.1.В результате изучения данного раздела студенты должны:
а. понимать природу нового типа сопротивления – реактивного, а также различие между омическим сопротивлением цепи постоянного тока и активным сопротивлением цепи переменного тока;
б. обратить внимание на условия применимости законов Ома и законов Кирхгофа к расчёту цепей переменного тока, поняв в чём состоит отличие;
в. усвоить понятие – «сдвиг фаз между током и напряжением» и запомнить, какие фазовые сдвиги вносят реактивные индуктивные и реактивные ёмкостные составляющие полного сопротивления электроприёмника;
г. разбираться в векторных диаграммах и уметь их строить для различных цепей переменного тока, при этом уметь использовать их в качестве количественного метода расчёта цепи переменного тока;
д. познакомиться с энергетическими процессами, протекающими в цепи переменного тока и мощностями их выражающими;
е. уметь проводить расчёт электрических цепей с последовательным соединением электроприёмников методом полного сопротивления, с параллельным соединением - методом проводимостей или векторной диаграммы, со смешанным соединением - методом проводимости и полного сопротивления или методом комплексных амплитуд.
Задача 2. Пусть в сеть переменного тока напряжением U включена цепь, схема которой показана на рис.6. Сопротивления всех элементов известны, необходимо найти действующие значения токов в цепи и мощности: полную, активную и реактивную.
|

Рис.6
РЕШЕНИЕ
1. Вычисляем активные и реактивные проводимости ветвей, включенных между узлами b и c.
· активная проводимость 2-й ветви

· активная проводимость 3-й ветви

· реактивная проводимость 2-й ветви (индуктивная)
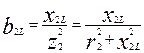
· реактивная проводимость 3-й ветви (емкостная)
 (т.к.
(т.к.  )
)
2. Полная проводимость участка bc:

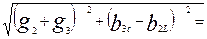
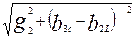
3. Находим активную и реактивную составляющие полного сопротивления участка bc.



На данном этапе решения исходную электрическую цепь можно представить схемой замещения, изображенной на рис.7. Она состоит из трёх электроприёмников (двух активных и одного реактивного), соединённых последовательно. Таким образом, появляется возможность определить полное сопротивление исходной цепи, свернув её эквивалентным путём к простейшему виду (Рис.8)
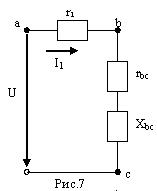

4. Полное сопротивление цепи.

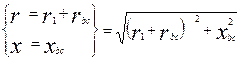
5. На основании закона Ома для действующих значений находим 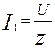
6. Находим напряжение на участке bc. Как видно из Рис.7
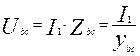

.
7. Возвращаемся к исходной цепи (Рис. 6.) Находим токи:
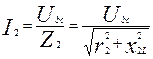 ;
; 
8. Полная мощность цепи: 
9. Активная мощность может быть найдена как сумма мощностей активных сопротивлений r1 и r2 (сумма активных мощностей

10. Реактивную мощность находим как алгебраическую сумму реактивных мощностей (мощностей реактивных сопротивлений

Замечание: Активную P и реактивную Q мощности можно найти исходя из знания угла сдвига фаз φ между напряжением U и током всей цепи I1

 ,
,
где  ;
; 
 - полное активное сопротивление цепи,
- полное активное сопротивление цепи, 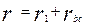
 - полное реактивное сопротивление цепи
- полное реактивное сопротивление цепи 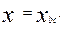
 - полное сопротивление цепи
- полное сопротивление цепи
11. Строим векторную диаграмму токов и напряжений. Её построение начинаем с построения векторной диаграммы токов для параллельного участка bc.
а) Проводим базисный вектор напряжения  . См Рис.9;
. См Рис.9;
б) под углом 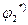 в сторону отставания по фазе (отставание здесь обусловлено индуктивной составляющей сопротивления второй ветви) строится вектор тока
в сторону отставания по фазе (отставание здесь обусловлено индуктивной составляющей сопротивления второй ветви) строится вектор тока  ;
;

Рис.9
в) под углом  по отношению к вектору
по отношению к вектору  в сторону опережения по фазе (т.к. характер сопротивления третьей ветви чисто ёмкостной) строится вектор
в сторону опережения по фазе (т.к. характер сопротивления третьей ветви чисто ёмкостной) строится вектор 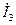 ;
;
г) на основании 1-го закона Кирхгофа  . Поэтому вектор
. Поэтому вектор  строим как сумму векторов
строим как сумму векторов 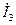 и
и  (по правилу параллелограмма);
(по правилу параллелограмма);
д) далее переходим к построению векторов напряжений (векторной диаграммы напряжений). Строим вектор 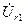 падения напряжения на активном сопротивлении r1. Направление этого вектора совпадает с направлением вектора тока
падения напряжения на активном сопротивлении r1. Направление этого вектора совпадает с направлением вектора тока  (сдвиг фаз между ними равен нулю).
(сдвиг фаз между ними равен нулю).
е) завершаем построение векторной диаграммы, построением вектора полного напряжения  . По второму закону Кирхгофа:
. По второму закону Кирхгофа:
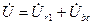

*) 
ЗАМЕЧАНИЕ. Углом сдвига фаз 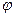 между полным током и полным напряжением является угол между векторами
между полным током и полным напряжением является угол между векторами  и
и  . Косинус этого угла ( cos
. Косинус этого угла ( cos 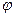 ) есть коэффициент мощности цепи.
) есть коэффициент мощности цепи.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 4141; Нарушение авторских прав?; Мы поможем в написании вашей работы!