Статистическое толкование энтропии

Изменение энтропии в изопроцессах идеального газа

Изохорный (V=const)	Изобарический (P=const)	Изотермический (T=const)	Адиабатический (S=const)

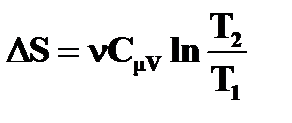
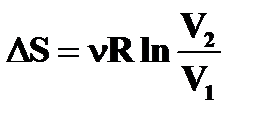
Термодинамическая вероятность W состояния тела или системы – это число способов, которыми может быть реализовано данное конкретное термодинамическое состояние (макросостояние). Иначе говоря, это число всевозможных микрораспределений частиц по координатам и скоростям (микросостояний), которыми может быть осуществлено данное макросостояние.

В качестве примера рассмотрим сосуд, в котором находятся три молекулы 1, 2, 3. Эти молекулы могут по-разному распределяться между правой и левой половинами сосуда.

´1 ´3 ´2	Возможные способы распределения этих молекул приведены в таблице. Здесь мы исходим из естественного предположения, что каждая молекула с равной вероятностью может находиться как в левой, так и в правой половине сосуда. Это следует из так называемого постулата равновероятности: в равновесной изолированной системе все микросостояния равновероятны.
Молекулы, находящиеся слева	1, 2, 3		1, 2	1, 3	2, 3
Молекулы, находящиеся справа		1, 2, 3				2, 3	1, 3	1, 2
Номер макро-состояния	I	II	III	IV
Статистиче-ский вес

Макросостояния определяются числом частиц в каждой половине сосуда. В нашем случае возможны четыре макросостояния: I, II, III и IV. Макросостояния характеризуются номерами частиц в каждой половине сосуда. Из таблицы видно, что макросостояниям I и II соответствует по одному микросостоянию. Статистический вес этих макросостояний равен 1. Статистический вес макросостояний III и IV равен 3, так как каждое из них может быть осуществлено тремя способами.

Таким образом, наибольшую термодинамическую вероятность или статистический вес имеют те макросостояния, в которых молекулы распределены по всему объему сосуда. Переход от порядка (все молекулы в одной части сосуда) к беспорядку (молекулы беспорядочно распределены по всему объему) повышает термодинамическую вероятность W состояния. Например, при движении с трением механическая энергия переходит во внутреннюю энергию, так как механическое движение упорядочено и обладает меньшей вероятностью, чем неупорядоченное тепловое движение молекул тела.

Следовательно, термодинамическая вероятность W является мерой беспорядка, мерой нестройности в системе.

Из сказанного следует, что наибольшей термодинамической вероятностью обладает равновесное состояние системы, состояние теплового равновесия. Поэтому если система, предоставленная самой себе, в некоторый момент времени не находится в состоянии равновесия, то наиболее вероятным будет ее приближение к равновесию. Если система перешла в состояние равновесия, то самопроизвольный переход ее в неравновесное состояние, строго говоря, не невозможен, но имеет подавляюще малую вероятность. В этом заключается природа необратимости тепловых процессов, которая проявляется в стремлении систем перейти в равновесное состояние.

Больцман сформулировал следующее утверждение: все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния.

Это утверждение носит название второго начала термодинамики и выражает статистический характер этого закона.

Формула Больцмана:

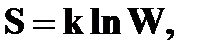
где k – постоянная Больцмана.

Энтропия системы определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние, т.е. энтропия является мерой неупорядоченности системы: чем больше микросостояний, реализующих данное макросостояние, тем больше энтропия.

Принцип возрастания энтропии: все процессы в замкнутой системе ведут к увеличению её энтропии. В замкнутой системе процессы идут в направлении от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной. В состоянии равновесия – наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.

Дата добавления: 2015-05-06