Работа процессов цикла Карно

Теорема Карно

Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей T₁ и холодильников T₂, наибольшим КПД обладают обратимые машины. При этом КПД обратимых машин, работающих при одинаковых температурах нагревателей и холодильников, равны друг другу и не зависят от природы рабочего тела, а определяются только температурами нагревателя и холодильника.

Наиболее экономичный обратимый процесс, состоящий из двух изотерм и двух адиабат – цикл Карно.

Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем. Последовательные термодинамические процессы в цикле Карно: 1 – изотерма – 2 – адиабата – 3– изотерма – 4 – адиабата – 1.

Процесс	Работа
Изотермическое расширение 1 – 2 T = const; V2>V1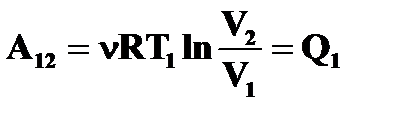
Адиабатическое расширение 2 – 3 dQ = 0; T2<T1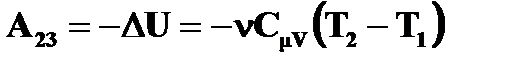
Изотермическое сжатие 3 – 4 T = const; V4<V3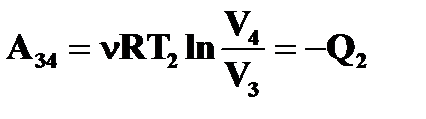
Адиабатическое сжатие 4 – 1 dQ = 0; T1>T2

Работа, совершаемая в результате кругового процесса:

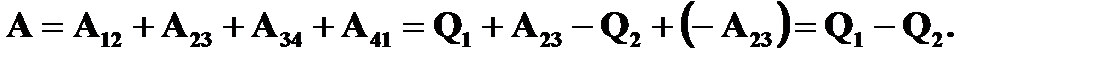
Для адиабат 2 – 3 и 4 – 1 уравнения Пуассона:

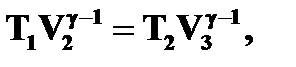
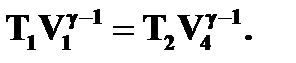
Откуда

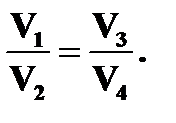
Получим термический КПД цикла Карно:

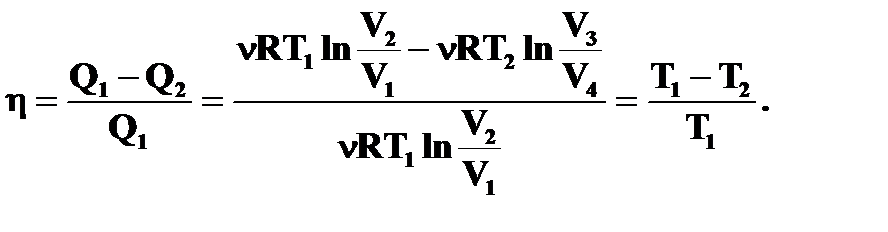
Последнее выражение можно вывести и другим способом:

Совершив цикл, система возвращается в исходное состояние, поэтому полное изменение энтропии за цикл DS=0. С другой стороны, полное изменение энтропии DS складывается из изменения энтропии в каждом отдельном процессе:

DS = DS₁₂ + DS₂₃ + DS₃₄ + DS₄₁.

При адиабатических процессах BC и DA, происходящих без теплообмена, DS₂₃=0 и DS₄₁=0. При изотермическом процессе, как было показано выше, 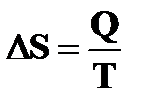, поэтому 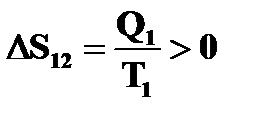(рабочее тело получает тепло Q₁ от нагревателя), 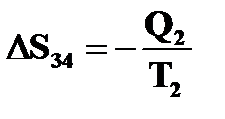(DS₃₄<0, т.к. рабочее тело отдает тепло Q₂ холодильнику).

Тогда ,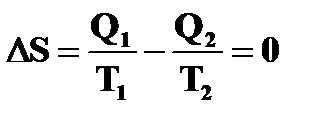

откуда .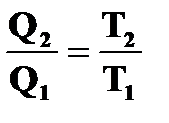

Выражение для коэффициента полезного действия тепловой машины 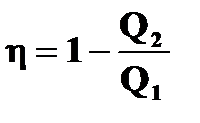с учетом последнего выражения можно представить в виде

.

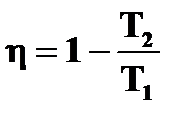Таким образом, коэффициент полезного действия всех тепловых машин, работающих по обратимому циклу Карно, не зависит от вида рабочего тела, а определяется температурами нагревателя Т₁ и холодильника Т₂. Это утверждение носит название теоремы Карно.

Рассмотрим теперь необратимый цикл Карно. при любом необратимом процессе 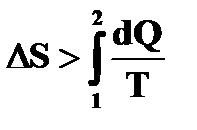. Следовательно, при необратимых изотермических процессах AB и CD

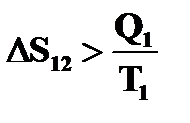и .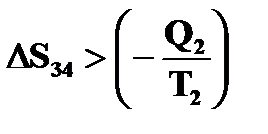

Перепишем DS₁₂ и DS₃₄ в виде:

, ,

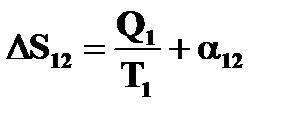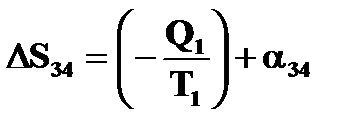где a₁₂ > 0 и a₃₄ > 0.

При необратимых адиабатических процессах 2-3и 4-1изменение энтропии DS₂₃ и DS₄₁ представим как DS₂₃=a₂₃>0 и DS₄₁=a₄₁> 0.

Полное изменение энтропии за цикл, в результате которого рабочее тело вернулось в исходное состояние, должно быть равно нулю, т.е.

_.

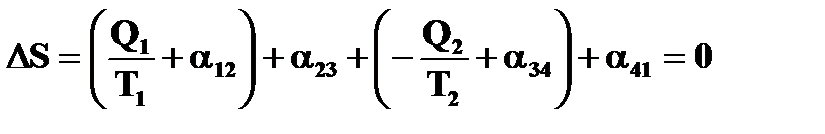Отсюда .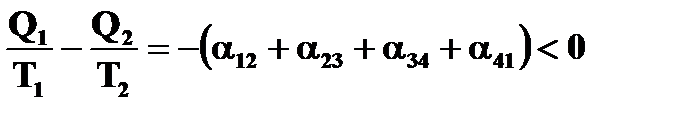

следовательно, ,

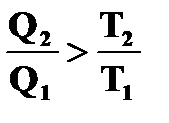
и < .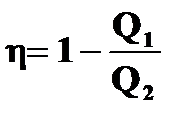

Коэффициент полученного действия необратимой машины всегда меньше, чем обратимой, работающей в тех же условиях.

В общем случае

.

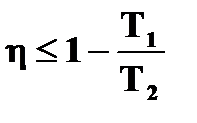Знак «=» относится к обратимому, знак «<» — к необратимому циклу карно.

Дата добавления: 2015-05-06