БИЛеТ №7

Необходимость эквивалентных схем

БИЛЕТ №6

1) Эквивале́нтная схе́ма (схема замещения, эквивалентная схема замещения) — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.

Одной из основных задач электроники является расчет электрических схем, то есть получение детальной количественной информации о процессах, происходящих в этой схеме. Однако рассчитать произвольную схему, состоящую из реальных электронных компонент, практически невозможно. Мешает расчету то обстоятельство, что попросту не существует методик математического описания поведения реальных электронных компонент (например, транзистора) как единого целого. Имеются значения отдельных параметров и экспериментально снятые зависимости, но связать их в единую точную формулу, полностью описывающую поведение компоненты, в большинстве случаев не представляется возможным.

С другой стороны, исключительно простым математическим аппаратом описываются идеализированные базовые элементы электронных схем (например, идеальный резистор). Однако они не существуют в реальном мире. Так, любой резистор имеет множество паразитных параметров: индуктивность, емкость, температурные зависимости и т.п.

Введение понятия эквивалентная схема позволяет «связать» мир реальных компонент и мир их идеальных приближений. Эквивалентная схема представляет собой цепь только из идеальных компонент, которая функционирует примерно также, как и исходная схема. В эквивалентной схеме могут быть отражены, при необходимости, различные паразитные эффекты: утечки, внутренние сопротивления и т.д. Эквивалентная схема может составляться как для одного элемента, так и для сложной цепи.

Электронный тракт описываете: набором конструктивных параметров, которыми являются параметры усилительных и преобразующих элементов.

Влияние обратной связи на параметры и характеристики усилительного тракта. При введении в усилительный тракт обратной связи его передаточные и другие свойства изменяются по сравнению с исходными. Эти изменения обусловлены двумя причинами. Первая причина – изменение конфигурации схемы из-за введения в схему цепи ОС, вторая – проявление действия самой ОС из-за создания условия прохождения сигнала с выхода на вход.

2) IMG0015, Хорвиц стр 184

1) Линейные искажения не нарушают амплитудных соотношений в усиливаемом сигнале. На рис. 4.1а. показаны амплитудные характеристики (то есть зависимости выходного напряжения от входного) идеальных усилителей с различными коэффициентами усиления. При наличии в усилителе линейных искажений сигнала, амплитудная характеристика не претерпевает никаких искажений. Тем не менее, линейные искажения, разумеется, искажают усиливаемый сигнал. Эти искажения связаны с неравномерностью амплитудно-частотной характеристики усилителя и нелинейности его фазо-частотной характеристики. В связи с этим, линейные искажения часто называют частотными. Главным признаком линейных искажений является то, что они не вызывают появления в спектре выходного сигнала новых составляющих. В результате влияния линейных искажений, могут лишь изменяться уровни его отдельных спектральных (частотных) составляющих.

Рис. 4.1 Передаточные характеристики и производимые ими искажения

Поскольку линейные искажения обычно вызывают нарушения амплитудно-частотной характеристики — как правило, их величина определяется именно способом исследования этой характеристики усилителя. Тем не менее, как уже было сказано выше, линейные искажения могут вызываться и нарушением линейности фазо-частотной характеристики усилителя, что проявляется в неодинаковости времени распространения различных частотных составляющих усиливаемого сигнала. Громкоговоритель с системой разделения спектра звукового сигнала и аналоговые магнитофоны хорошо демонстрируют это явление.

Неплохим способом выявления заметных линейных искажений в усилителе, является подача на его вход импульсов прямоугольной формы и наблюдение формы выходного сигнала при помощи осциллографа. Передний фронт сигнала прямоугольной формы очень чувствителен как к нарушениям равномерности амплитудно-частотной характеристики, так и к нарушениям линейности фазо-частотной характеристики. В случае заметных линейных искажений, форма прямоугольных импульсов на выходе усилителя будет существенно нарушена, что легко видно на экране осциллографа. Такой простой тест в какой-то степени является альтернативой необходимости исследования амплитудно-частотной и фазо-частотной характеристик усилителя.

При генерации импульсных сигналов различной формы необходимо формирование временных интервалов, задающих длительность импульсов и пауз, частоту повторения импульсов и т.п. Эта задача решается с помощью формирующих цепей содержащих реактивные элементы. Наиболее простыми и надежными являются RC-цепи. Как правило, они применяются в качестве разделительных, дифференцирующих или интегрирующих цепей.

Схема разделительной цепи приведена на рис. 16.1а. Временные диаграммы напряжений в схеме приведены на рис 16.1б. При анализе процесса формирования напряжения на выходе RC- цепи будем полагать, что внутреннее сопротивление источника входного напряжения равно нулю, а сопротивление нагрузки - бесконечно большое. Емкость С не пропускает на выход постоянную составляющую источника питания. Поэтому цепь названа разделительной.

Пусть в момент t= 0 на вход цепи (зажимы 1 -1^') поступает прямоугольный импульс амплитудой U_m и длительностью t_u. В начальный момент времени конденсатор С разряжен и ток в RC - цепи определяется только амплитудой импульса U_m и сопротивлением R. Поэтому на зажимах 2 - 2^' создается напряжение равное максимальному . По мере заряда конденсатора С ток в цепи, а значит и напряжение на выходе будет экспоненциально убывать:

, (16.1)

где t_ц = R × C [с] - постоянная цепи.

К моменту окончания импульса (когда t = t_u) выходное напряжение упадет до U_вых(t_u), причем

. (16.2)

После окончания импульса напряжение на входе цепи U_вх = 0. Поэтому конденсатор С начинает разряжаться через источник U_вх и резистор R. Ток разряда создает на выходе цепи отрицательный перепад напряжения, причем:

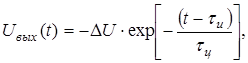
Где

. (16.3)

Разделительная цепь должна передавать импульс от входа к выходу с возможно меньшими искажениями его формы. Искажение формы оценивают максимальным относительным снижением вершины выходного импульса.

.

Из выражения (16.3) следует, что D U тем меньше, чем больше U_вых(t_u), а U_вых(t_и) тем больше, чем меньше отношение t_u/t_ц (см рис.16.2). Если требуется чтобы максимальное относительное снижение вершины импульса не превышало 1%, то постоянная времени цепи t_ц должна превышать длительность импульса t_u не менее чем в 100 раз.

Схема дифференцирующей цепи такая же, как и схема разделительной цепи. Но дифференцирующая цепь предназначена для укорочения импульсов или для выделения их фронта и среза. Эта задача решается тем лучше, чем больше отношение t_u/t_ц. Реально оно находится в пределах от 10 до 100. Выходное напряжение представляет два биполярных импульса совпадающих по времени с фронтом и срезом входного импульса (рис. 16.1б). Амплитуда биполярных импульсов затухает экспоненциально в соответствии с (16.1). Длительность этих импульсов на уровне 0,05 U_m. t_вых» 3 t_ц. Подбором t_ц ее можно сделать сколь угодно малой.

Схема интегрирующей цепи приведена на рис. 16.2а. На рис. 16.2б приведены диаграммы напряжений на входе и выходе цепи. При поступлении на вход такой цепи (зажимы 1 - 1^') прямоугольного импульса напряжения выходной сигнал нарастает по экспоненте

. (16.4)

Время необходимое для нарастания выходного сигнала до уровня 0,9 U_m, составляет 2,3 t_ц, а до уровня 0,99 U_m - 4,6 t_ц.

Срез убывает по экспоненциальному закону:

,

где

.

На начальном участке выходное напряжение изменяется по закону, близкому к линейному. Этот участок часто используется для линейного накопления напряжения сигнала. Поэтому рассматриваемая цепь получила название интегрирующей. Чтобы цепь работала как интегрирующая, отношение t_u/t_ц должно быть значительно меньше единицы.

Дата добавления: 2015-05-06