Анализ переходных характеристик

Электрический импульс — кратковременный всплеск электрического напряжения или силы тока в определённом, конечном временном промежутке. Различают видеоимпульсы — единичные колебания какой-либо формы и радиоимпульсы — всплески высокочастотных колебаний.

Формирование импульсов - это изменение параметров исходного сигнала с целью получения импульсов с заданными параметрами.

Генерирование импульсов - автономное преобразование энергии источника питания в энергию требуемой последовательности импульсов или единичных импульсов.

В установившемся режиме токи и напряжения всех ветвей электрической цепи изменяются по периодическому закону или в частном случае сохраняют неизменные значения. Всякое изменение как топологии цепи, так и параметров входящих в нее элементов нарушает периодический характер изменения токов и напряжений ветвей, т.е. приводит к тому, что режим работы становится неустановившимся. Любое скачкообразное изменение в цепи, нарушающее установившийся режим, называется коммутацией. Если внешнее воздействие на цепь и после коммутации имеет периодический характер, то с течением времени цепь перейдет в новый установившийся режим. Неустановившиеся процессы, которые имеют место в цепи при переходе от одного установившегося режима к другому, называется переходными. Переход реальной электрической цепи от одного установившегося режима к другому не может происходить мгновенно, скачком. Это объясняется тем, что каждому установившемуся состоянию соответствует определенное значение энергии, запасенной в электрическом и магнитном полях. Скачкообразный переход от одного установившегося режима к другому потребовал бы скачкообразного изменения запасенной энергии, что возможно, если источники энергии обладают бесконечно большой мощностью, т.е. отдаваемые ими токи или напряжения могут принимать бесконечно большие значения. В связи с тем, что реальный источник энергии может отдавать только конечную мощность, суммарная энергия, запасенная в цепи, может изменяться только плавно, т.е. представляет собой непрерывную функцию времени. Таким образом, возникновение переходных процессов при переходе электрической цепи от одного установившегося состояния к другому связано с тем, что энергия, запасенная реактивными элементами цепи, не может изменяться скачком, а изменяется только плавно, т.е. с конечной скоростью.

Законы коммутации:

1) в начальный момент времени после коммутации ток индуктивности сохраняет такое же значение, как и непосредственно перед коммутацией: 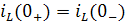, а затем плавно изменяется начиная с этого значения.

2) В начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: , а затем плавно изменяется начиная с этого значения.

Переходной характеристикой цепи h(t) называют отношение отклика цепи y(t) (например, выходное напряжение U_y(t)) к величине X ступенчатого воздействия 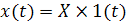(например, входного напряжения 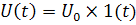) при нулевых начальных условиях, т.е. ,

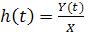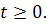
Существует ряд аналитических методов расчета переходных характеристик: классический, операторный, метод Дюамеля.

Классический метод сводится к составлению и решению дифференциального уравнения, устанавливающего связь между входным и выходным сигналом.

Метод интеграла Дюамеля используется при произвольном воздействии сложной формы на входе цепи. В основе метода лежит принцип наложения. Суть метода: разбиение отклика на сумму, заменить ступенчатой функцией, после чего найти отклик на каждую ступень, затем просуммировать с помощью интеграла Дюамеля отклики.

Операторный метод нахождения переходных процессов основан на использовании прямого и обратного преобразования Лапласа, и связан с решением алгебраических уравнений относительно изображения.

Основные этапы анализа переходных процессов операторным методом:

1) Анализ цепи до коммутации и определение независимых начальных условий. Задание на вход цепи единичный скачок напряжения 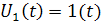. С помощью таблиц или преобразование Лапласа найти изображение скачка:

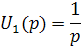
Где 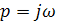- оператор Лапласа

2) Составление операторной схемы замещения цепи после коммутации. Составление операторной схемы замещения цепи производится непосредственно по схеме замещения цепи для мгновенных значений путем замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений идеализированных источников тока или напряжения их операторными изображениями.

3) Составление уравнений электрического равновесия цепи в операторной форме.

4) Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений.

5) Определение оригиналов искомых токов и напряжений. Как правило, определение оригиналов искомых токов и напряжений производится путем применения таблиц обратного преобразования Лапласа с учетом основных свойств преобразования Лапласа. Если изображение интересующей функции представляет собой отношение двух полиномов p, для выполнения обратного преобразования Лапласа можно воспользоваться теоремой разложения.

Теорема разложения. Если изображение искомого тока или напряжения имеет вид рациональной дроби

Причем многочлены (относительно p) 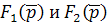удовлетворяют следующим условиям: степень 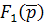ниже степени 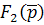, a_k и b_k – вещественные числа, а корни p₁,p₂,…, p_n уравнения 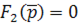различны, то оригинал определяется выражением

Если знаменатель уравнения 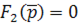имеет один корень, равный нулю, т.е. 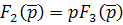, то оригинал находится по формуле

Если в выше приведенном уравнении 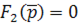имеет n различных корней (p₁,p₂,…, p_s) и из них корень p₁ кратностью m₁, корень p₂ кратностью m₂, корень p_s, то по изображению 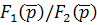оригинал вычисляют по формуле

Здесь выражение, стоящее в знаменателе квадратной скобки, надо сначала сократить на 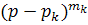и лишь после этого дифференцировать.

Формулу (7.2) можно также записать:

Если уравнение 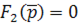содержит одновременно и простые, и кратные корни, то для определения слагаемых, соответствующих простым корням, используется формула (7) или (7.1), если имеется простой корень p=0, для кратных - формула (7.2 или 7.3).

Временными параметрами, характеризующими переходную характеристику, являются постоянная времени τ и время установления t_уст.

Постоянная времени вводится для экспоненциальной функции вида: 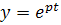, где p 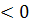. Постоянная времени характеризует скорость изменения экспоненциальной функции на начальном этапе. Под постоянной времени цепи понимают время, за которое выходной сигнал, изменившийся по закону 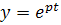, уменьшается в 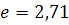раз, т.е. до уровня 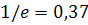от своего начального значения.

Время установления – это время, за которое переходная характеристика достигает своего стационарного значения с заданной точностью. Функция, уменьшающая по закону 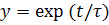за время 3τ, достигает своего стационарного значения с точностью 5%. Если нет особых оговорок, то за время установления принимают 3τ (t_уст=3τ).

Воздействие в виде прямоугольного импульса может рассматриваться как наложение сдвинутых во времени на длительность импульса противоположных по знаку скачков напряжения:

Реакция цепи на такое импульсное воздействие также представляется наложением сдвинутых во времени на t_и реакций цепи на указанные скачки

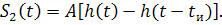
2) IMG0022

Дата добавления: 2015-05-06