Нестационарное уравнение Шредингера

Перейдем теперь к изучению гармонического осциллятора на основе нестационарного уравнения Шредингера. С квантомеханической точки зрения для того, чтобы проследить движение частицы в гармоническом поле, мы должны решить уравнение Шредингера:

(20)

Выберем волновую функцию начального состояния в виде гауссового пакета:

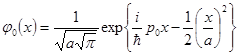. (21)

Такая волновая функция соответствует частице, локализованной вблизи точки x=0 и имеющей импульс p₀. Пусть также ширина пакета 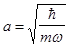. Решение задачи (20) ищется в виде разложения по собственным функциям (18) в виде:

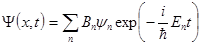. (22)

Коэффициенты разложения B_n и есть амплитуды вероятности обнару-

жить осциллятор в состоянии n. В результате вычислений получим для

вероятности обнаружить осциллятор в состоянии n:

|B_n|² = 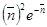, (23) где 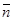= 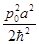- среднее число квантов в начальном состоянии.

Так как энергия начального состояния равна

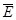
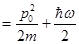, (24)

а величина 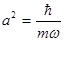, получим: Ē= ħω 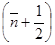. (25) Поскольку среднее число квантов 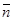от времени не зависит, в процессе эволюции начального состояния его средняя энергия не изменяется, не изменяется и распределение вероятностей обнаружить частицу в том или ином состоянии осциллятора. Такие нестационарные состояния называются когерентными. Подставив B_n в (22), можно определить волновую функцию когерентного состояния. Плотность вероятности обнаружить частицу в различных точках пространства равна :

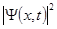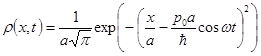, (26)

и, как видно, соответствует осциллирующему гауссовому пакету с неизменной шириной a. Определение средних значений координаты и импульса частицы приводит нас к выражениям

,

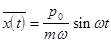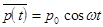, (25)

совпадающим с классическими зависимостями координаты и импульса частицы во времени. Таким образом, “в среднем” квантовая частица опять движется по классическим законам. При этом, если ширина распределения

a мала по сравнению с амплитудой колебаний x₀, то движение квантового осциллятора практически неотличимо от движения осциллятора классического.

Поскольку пакет гауссовой формы обладает минимальным произведением неопределенностей импульса и координаты, то рассматриваемый нами случай наиболее близок к классическому. Следует отметить, что сохранение формы пакета возможно только в том случае, если 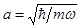. В противном случае ширина пакета будет меняться во времени с частотой 2w, но сам пакет будет сохранять гауссову форму и не расплываться с течением времени. Последнее свойство пакета есть особенность гармонического потенциала. В любом другом потенциале пакет расплывается - частица постепенно делокализуется в пространстве.

Остановимся еще на важном частном случае рассмотренной задачи. Пусть начальное значение импульса равно нулю. Тогда из решения задачи о гармоническом осцилляторе (26) получаем:

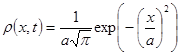, (27)

т.е. распределение вероятности обнаружить частицу в различных точках пространства не зависит от времени. Это основное стационарное состояние,

для которого 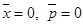, что соответствует классической частице, находящейся в положении равновесия.

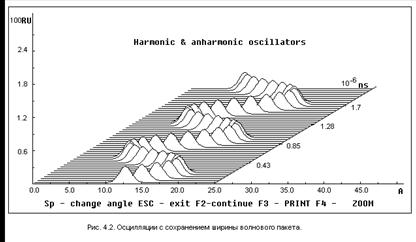
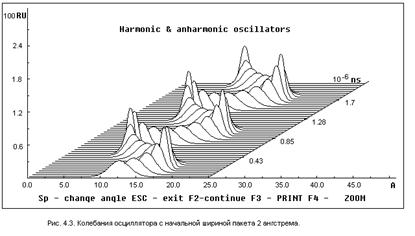
На рисунках 4.2 – 4.6 приведены решения задачи о движении квантовой частицы в гармоническом потенциале при различных параметрах начального волнового пакета. Так на рис. 4.2 приведены осцилляции пакета с шириной, совпадающей с шириной волновой функции основного состояния осциллятора 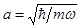, а на рис. 4.3 - осцилляции пакета, начальная ширина которого .

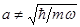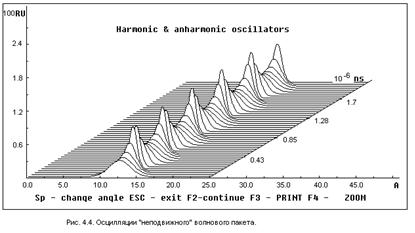
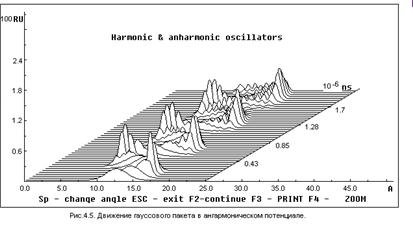
Особый интерес представляют осцилляции “неподвижного” пакета (p₀=0) в случае 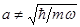. Хотя в этом случае 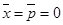, состояние, представленное на рис 4.4, является нестационарным и может быть представлено в виде суперпозиции различных стационарных состояний. На рис 4.5 приведены осцилляции пакета с теми же параметрами, что и на рис 4.2, но находящегося в ангармоническом потенциале вида

.

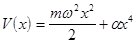Как видно, пакет не сохраняет свою форму, что соответствует делокализации частицы в пространстве.

Описание программы:

Программа Harmonic Oscillators демонстрирует движение волнового

пакета в гармоническом потенциале .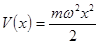

Частота ω в программе фиксирована и равна 8,162·10¹⁵ с^-1.

Параметры начального волнового пакета и потенциала, которые необходимо

задать перед запуском программы, указаны в меню лабораторной задачи (рис.

4.6). Величина импульса частицы, как и в других программах, связана с

выбираемой вами энергией соотношением .

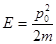Вы можете установить начальную ширину волнового пакета (окно Choose

Width), а также изменить форму начального пакета, выбрав его в виде

,

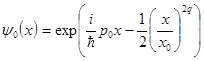где q¹1. Для этого в окне ChooseFormнужно ввести величину, не равную

единице. В данной программе имеется также возможность исследовать

движение частицы в ангармоническом потенциале вида

.

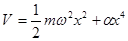В окне ChooseAnharmonismзначение α=0 соответствует гармоническому потенциалу. В случае изучения движения частиц в ангармоническом

потенциале (α ¹0) величина пространственного разрешения (Space

Resolution) должна быть равна 2или 3. Во всех рассмотренных случаях

можно наблюдать и движение классической частицы. В процессе работы на

экране терминала отображается вид потенциальной кривой V(x), величина

|Ψ(x)|² в относительных единицах, положение классической частицы в

разные моменты времени, текущее значение ширины пакета, если он гаус-сов, а потенциал гармонический (в других случаях отображается начальная

ширина пакета x₀) и величина энергии частицы E (рис.4.7). Максимальное время демонстрации ограничено величиной 1,5·10^-5 нс. Это связано с возможностью постепенного накопления ошибки вычислений и искажения физической картины процесса.

Дата добавления: 2015-03-29