Общая характеристика переходных процессов

Мощность в трехфазных цепях

Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.
Активная мощность трехфазной цепи равна сумме активных мощностей фаз

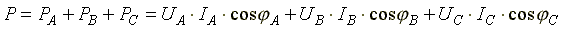(7.5)

Формула (7.5) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.
При симметричной нагрузке:

При соединении в треугольник симметричной нагрузки

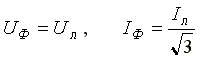
При соединении в звезду

.

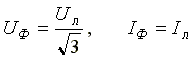В обоих случаях

.

8. Переходные процессы в линейных
электрических цепях

В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому.
Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.

Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации

i_L (0₊) = i_L (0_-),

где i_L (0₊) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
i_L (0_-) - ток в индуктивности непосредственно перед коммутацией.

Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.

u_C (0₊) = u_C (0_-),

где u_C (0₊) - напряжение на емкости в момент коммутации;
u_C (0_-) - напряжение на емкости непосредственно перед моментом коммутации.

Допущения, применяемые при анализе переходных процессов.

1. Полагают, что переходный процесс длится бесконечно большое время.

2. Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.

3. Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.

В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.

.

где i_пр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
i_св(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.

Свободный ток определяют по формуле:

.

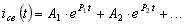Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме.
P₁, P₂ - корни характеристического уравнения.
А₁, А₂ - постоянные интегрирования, определяются с помощью начальных условий.
Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю.
Начальные условия могут быть независимыми или зависимыми.
Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости u_c(0) и ток в ветви с индуктивностью i_L(0) в момент коммутации.
Остальные начальные условия: напряжение и ток в ветви с сопротивлением u_R(0) и i_R(0), напряжение на индуктивности u_L(0), ток в ветви с емкостью i_C(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.

8.2. Переходные процессы в цепях
с одним реактивным элементом

Короткое замыкание в R-L цепи

На рис. 8.1 изображена электрическая цепь, в которой включен источник постоянной ЭДС. В результате коммутации рубильник замыкается и образуется замкнутый на себя R-L контур.

До коммутации по индуктивности протекал ток

Этот ток создавал постоянное магнитное поле в индуктивной катушке.

Определим закон изменения тока в индуктивности после коммутации.
В соответствии с классическим методом

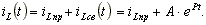
Принужденный ток после коммутации замыкается через рубильник, имеющий нулевое сопротивление, и через индуктивность не протекает. Индуктивный ток имеет только свободную составляющую

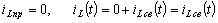
Магнитное поле, исчезая, индуктирует в индуктивной катушке ЭДС самоиндукции. Свободный ток в R-C контуре существует за счет этой электродвижущей силы.
Запишем уравнение для свободного тока в R-L контуре, используя второй закон Кирхгофа.

(8.1)

Ищем решение этого уравнения в виде экспоненты

.

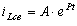Производная

.

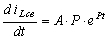Подставим значения свободного тока и производной тока в уравнение (8.1)

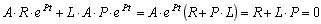(8.2)

Уравнение (8.2), полученное из уравнения (8.1), называется характеристическим.

- корень характеристического уравнения.

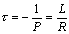- постоянная времени переходного процесса, измеряется в секундах.
Постоянная времени τ - это интервал времени, за который переходный ток уменьшается в e раз.

.

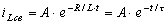Постоянную интегрирования А определяем с помощью начального условия.

В соответствии с первым законом коммутации,

.

Получим

Напряжение на индуктивности .

На рис. 8.2 изображены кривые переходного тока в ветви с индуктивностью и переходного напряжения на индуктивности. Переходный ток и напряжение по экспоненте стремятся к нулю. В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5)τ, переходный процесс заканчивается.

Подключение R-L цепи к источнику постоянной ЭДС

В схеме на рис. 8.3 до коммутации рубильник разомкнут. В результате коммутации рубильник замыкается и подключает R-L цепь к источнику постоянной ЭДС. Определим закон изменения тока i(t).

.

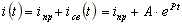Принужденный ток в установившемся режиме после коммутации

.

В свободном режиме из схемы исключен внешний источник питания. Схема на рис. 8.3 без источника ЭДС ничем не отличается от схемы на рис. 8.1.

Свободный ток определяется по формуле
.
Запишем значение переходного тока для момента
коммутации, (t = 0). ,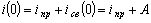
откуда .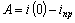

До коммутации рубильник был разомкнут, и ток в схеме отсутствовал.
Сразу после коммутации ток в индуктивности остается равным нулю.

.

.

.

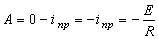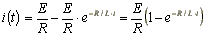Напряжение на индуктивности

.

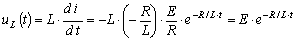На рис. 8.4 изображены кривые переходного, принужденного, свободного токов и переходного напряжения на индуктивности.

Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля. В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.
Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.

Дата добавления: 2015-05-06