I. Докажем существование плоскости

Теорема о трех перпендикулярах

Крупнейшие достижения

Возникновение кубизма

Возникновение кубизма традиционно датируют 1906 — 1907 г. и связывают с творчеством Пабло Пикассо и Жоржа Брака. Термин «кубизм» появился в 1908 г., после того как художественный критик Луи Восель назвал новые картины Брака «кубическими причудами» (фр. bizarreries cubiques).

Начиная с 1912 г. в кубизме зарождается новое ответвление, которое искусствоведы назвали «синтетическим кубизмом». Простую формулировку основных целей и принципов кубизма дать довольно трудно; в живописи можно выделить три фазы этого направления, отражающие разные эстетические концепции, и рассмотреть каждую в отдельности: сезанновский (1907—1909), аналитический (1909—1912) и синтетический (1913—1914) кубизм.

Наиболее известными кубистическими произведениями начала XX века стали картины Пикассо «Авиньонские девицы», «Гитара», работы таких художников, как Хуан Грис, Фернан Леже, Марсель Дюшан, скульптуры Александра Архипенко и др. Кубизм развивался и за пределами Франции; особенно плодотворно — в Чехословакии.

Теорема: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. Доказательство: пусть АВ - перпендикуляр к плоскости Альфа, АС - наклонная и с - прямая в плоскости Альфа, проходящая через основание С наклонной. Проведем прямую СА¹, параллельную прямой АВ. Она перпендикулярна плоскости Альфа. Проведем через прямые АВ и А¹С плоскость Бетта. Прямая с перпендикулярна прямой СА¹. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости Бетта, а значит, и прямой АС. Аналогично если прямая с перпендикулярна наклонной СА, то она, будучи перпендикулярна и прямой СА¹, перпендикулярна плоскости Бетта, а значит, и проекции наклонной ВС.

1. Теорема. Через две пересекающиеся прямые проходит единственная плоскость. Доказательство.

1) Пусть прямые а и b пересекаются в точке О (О=а∩b), Е – некоторая точка на прямой b, не совпадающая с точкой О.

2) Тогда по теореме 1 существует плоскость α, проходящая через точку Е и прямую а ().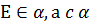

3) Точки О и Е прямой b лежат в плоскости α, следовательно, по аксиоме А2 плоскость α проходит через прямую b. Таким образом, существует плоскость α, проходящая через прямые а и b.

Дата добавления: 2015-03-29