II. Докажем, что такая плоскость единственная

1) Допустим, что существует еще одна плоскость β, проходящая через прямые а и b.

2) Точка Е лежит на прямой b, следовательно, плоскость β проходит через точку Е и прямую а. По теореме 1 через точку Е и прямую а проходит единственная плоскость, значит, плоскость β совпадает с плоскостью α. Теорема доказана.

3. Теорема (первый признак). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство.

Пусть ABC и A1B1C1 — треугольники, у которых АВ =А1В1,АС=А1С1 и <ВАС = <B1A1C1

1) Отложим <BlA1C1 в той же полуплоскости с границей АС, в которой лежит угол ВАС, так, что бы сторона совпала со стороной АС. Это возможно в силу аксиомы откладывания отрезка на луче и условия АС = А1С1.

2) Так как <BAC = <B1A1C1 то, согласно аксиоме откладывания угла в полуплоскость, лучи АВ и А1В1 совпадут.

3) Так как АВ =А1В1, то по аксиоме единственности откладывания отрезка на луче точка Вг совпадет с точкой В, кроме того, точка С совпадает с точкой C1. С учетом того, что через две точки проходит единственная прямая, получаем, что отрезки ВС и В1С1 совпадают. Таким образом, совпадают углы и стороны треугольников ABC и А1В1С1, значит, эти треугольники равны

Теорема доказана.

4. Теорема 1 (второй признак). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство.

1) Пусть ABC и AlBlCl два треугольника, у которых АС = А1С1, <A = <A1 и <C = <C1. Докажем, что треугольники ABC и AlBlCl равны.

2) Отложим угол В1А1С1 в той полуплоскости с границей АС, в которой лежит угол ВАС. Так как <A=<A1, то на основании аксиомы откладывания угла в полуплоскость лучи А1В1 и АВ совпадут, а поскольку АС = А1С1, то по аксиоме откладывания отрезка на луче точка С1 совпадет с точкой С. Угол B1C1A1 будет отложен в ту же полуплоскость от луча С А и, согласно аксиоме откладывания угла в полупл-ть. 3) Так как лучи А1В1 и С1В1 совпали соответственно с лучами АВ и СВ, то точка их пересечения В1 совпадет с точкой В. Следовательно, стороны и углы треугольника A1B1C1 совпадут со сторонами и углами треугольника АBС, а, значит, △АВС = △А1В1С1.

Теорема доказана.

5.Теорема 1 (признак параллельности прямых по равенству внутренних накрест лежащих углов). Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.

Доказательство.

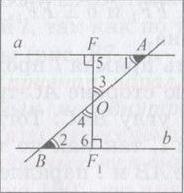
1) Пусть при пересечении прямых а и b секущей АВ внутренние накрест лежащие углы 1 и 2 равны (рис). Докажем, что а || Ь.

2) Если <1 = < 2 = 90°, a⊥AB, b⊥AB. Отсюда следует, что а || b.

3) Если <1 = <2 = 90°, то из середины О отрезка АВ проведем отрезок OF⊥а.

4) На прямой b отложим отрезок BF1 =AF и проведем отрезок OF1.

5) Заметим, что △OFA = △OF1B по двум сторонам и углу между ними (АО = ВО, AF = BF1 и <1 = <2). Из равенства этих треугольников следует, что <3 = <4 и <5 = <6.

6) Так как <3 = <4, а точки А, В и О лежат на одной прямой, то точки Fl, F и О также лежат на одной прямой.

7) Из равенства <5 = <6 следует, что <6 = 90°. Получаем, что а ⊥FF; и b ⊥ FF1, а а || b.

Теорема доказана.

6. Теорема 2 (признак параллельности прямых по равенству соответственных углов). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство.

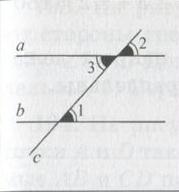
1) Пусть при пересечении прямых а и b секущей с соответственные углы равны, например <1 = <2. Докажем, что прямые а и b параллельны (рис).

2) Заметим, что <2 = <3 как вертикальные углы.

3) Из равенств <1 = <2 и <2 = <3 следует, что <1 = < 3. А поскольку углы 1 и 3 являются внутренними накрест лежащими углами, образованными при пересечении прямых а и b секущей с, то в силу теоремы 1 получаем, что а || b.

Теорема доказана.

7. Теорема 3 (признак параллельности прямых по сумме градусных мер внутренних односторонних углов). Если при пересечении двух прямых секущей сумма градусных мер внутренних односторонних углов равна 180°, то прямые параллельны.

Доказательство.

1) Пусть при пересечении двух прямых а и b секущей с сумма градусных мер внутренних односторонних углов равна 180°, например <1 + <2 = 180° (рис.).

2) Заметим, что <3 + <2 = 180°, так как углы 3 и 2 являются смежными.

3) Из равенств <l + <2 = 180° и <3 + <2 = 180° следует, что <1 = < 3.

4) Поскольку равны внутренние накрест лежащие углы 1 и 3, то прямые а и b параллельны.

Теорема доказана.

8. Опр. Внешним углом треугольника называется угол, смежный с каким-либо углом треугольника.

Теорема (о внешнем угле треугольника). Градусная мера внешнего угла треугольника равна сумме градусных мер двух углов треугольника, не смежных с ним.

Доказательство.

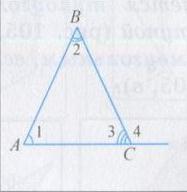
1) Пусть ABC — произвольный треугольник. Докажем, например, что градусная мера внешнего угла 4 равна сумме градусных мер не смежных с ним углов 1 и 2 (рис.).

2) Так как сумма градусных мер углов 3 и 4 равна градусной мере развернутого угла, то < 3 + < 4 = = 180°, а по теореме о сумме градусных мер углов треугольника (<l + <2) + <3 = 180°, следовательно, <4 = <1 + <2.

Теорема доказана.

10. Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

Доказательство.

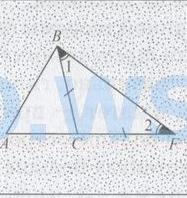
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ <АС + СВ (рис. 109, а).

2) Отложим на луче АС отрезок CF, равный стороне ВС (рис.).

3) В равнобедренном треугольнике BCF угол 1 равен углу 2, а в треугольнике ABF ZABF > Z1, следовательно, верно неравенство <ABF > < 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ < AF. Но так как AF = АС + CF, то АВ < АС + СВ.

Теорема доказана.

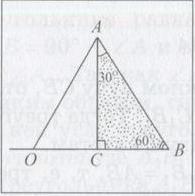
9. Свойство 1 (свойство катета, лежащего против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

Доказательство.

1) Пусть АС В — прямоугольный треугольник, в котором <C = 90°, < А = 30°. Докажем, что катет ВС равен половине гипотенузы АВ (рис.).

2) Так как сумма градусных мер углов треугольника равна 180°, то в прямоугольном треугольнике АСВ <ABC = 60°.

3) Пусть точка О лежит на луче ВС так, что СО = СВ. Тогда прямоугольные треугольники АСО и АСВ равны по двум катетам (катет АС — общий, СО = СБ), следовательно, <AOB = 60°.

4) В треугольнике АОВ выполняются равенства <АОВ = <OAB = 60°, а, значит, стороны, лежащие против этих углов, равны, т. е. АВ = ОВ. Так как

С В =1\2ОВ, следовательно, СВ = 1\2АВ.

Свойство доказано.

Дата добавления: 2015-03-29