Чита-2012

Динитрофторбензол (с последующим гидролизом и анализом образовавшихся веществ)

Сахарозы

Гликозидная

Сахароза

Не обладает восстановительными свойствами

Пропеновая кислота

Этиламин

Минеральными кислотами и основаниями

Диастереомерами

261. Амфотерность аминокислот проявляется во взаимодействии с:

262. Какое вещество получается при декарбоксилировании α-аминопропановой кислоты (аланина) :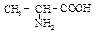

263. Какое вещество получается при нагревании β-аминопропановой кислоты:

264. В растворе фенилаланина с рН=рI существует в виде:

1) биполярного иона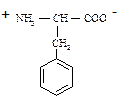

265. Ксантопротеиновая реакция – это:

1) качественная реакция на ароматическое кольцо (+HNO₃),

266. Какие из утверждений не соответствуют свойствам мальтозы:

267. Дисахарид 1,2-α-D- глюкопиранозидо-β-D-фруктофуранозид:

268. Какая гликозидная связь характерна для крахмала:

269. Явление инверсии характерно для:

270. N-концевые аминокислоты в пептидах и белках можно определить с помощью реагента:

Задание № І. Даны в алгебраической форме два числа a и b:

а) Найти алгебраическую форму числа = a/b;

б) Найти тригонометрическую форму числа ;

в) Решить уравнение z³+ =0

г) Изобразить числа , - и полученные корни уравнения z³+ =0 точками на комплексной плоскости.

	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =
	a = b =		a = b =

Задание № ІІ. Указать на комплексной плоскости все точки z, для которых выполняется неравенство. Сделать чертёж.

Задание № ІІІ. Найти сумму, разность, произведение и частное чисел a и b в алгебраической форме. Найти тригонометрическую форму этих чисел. Найти их произведение и частное в тригонометрической форме.

Дата добавления: 2015-03-29