Среднего темпа прироста

Этап выполнения статистических расчетов

Задание 1.

Расчёт и анализ показателей ряда динамики выпуска продукции за шестилетний период.

Выполнение Задания 1 заключается в решении двух задач:

Задача 1. Расчет цепных и базисных показателей динамики: абсолютный прирост (сокращение); темп роста (снижения); темп прироста (сокращения) и абсолютное значение 1 % прироста.

Задача 2. Расчет средних показателей ряда динамики: средний уровень ряда динамики; средний абсолютный прирост; средний темп роста и средний темп прироста.

Алгоритмы выполнения Задания 1

Задача 1.. Расчет цепных и базисных показателей динамики: абсолютный прирост (сокращение); темп роста (снижения); темп прироста (сокращения) и абсолютное значение 1 % прироста

Алгоритм 1.1. Расчёт цепных и базисных показателей динамики, характеризующих изменение отдельных уровней ряда динамики

1. В ячейке, выделенной для значения абсолютного прироста цепного за первый год (С26), перед формулой поставить знак равенства «=»;

2. Enter;

3. Установить курсор в правом нижнем углу ячейки (С26) с формулой – образцом (курсор примет форму черного крестика) и, удерживая левую клавишу мыши в нажатом состоянии, переместить курсор до нижней клетки графы. Отпустить клавишу мыши (формула – образец размножилась на всю графу).

4. Выполнить действия 1–2 поочередно для всех аналитических показателей ряда динамики табл.3.2:

абсолютного прироста базисного;

темпа роста цепного и базисного;

темпа прироста цепного и базисного;

абсолютного значения 1% прироста.

Результат работы алгоритма 1.1 для демонстрационного примера приведены в табл. 3.2–ДП.

	A	B	C	D	E	F	G	H	I
	Таблица 3.2–ДП
	Показатели динамики выпуска продукции
	Годы	Выпуск продукции, млн. руб.	Абсолютный прирост, тыс. тонн	Темп роста, %	Темп прироста, %	Абсолютное значение 1 % прироста
	цепной	базисный	цепной	базисный	цепной	базисный
	1-й	3020,00
	2-й	3260,00	240,00	240,00	107,9	107,9	7,9	7,9	30,2
	3-й	3650,00	390,00	630,00	112,0	120,9	12,0	20,9	32,6
	4-й	3530,00	-120,00	510,00	96,7	116,9	-3,3	16,9	36,5
	5-й	3765,00	235,00	745,00	106,7	124,7	6,7	24,7	35,3
	6-й	4077,00	312,00	1 057,00	108,3	135,0	8,3	35,0	37,65

Задача 2. Расчет средних показателей ряда динамики: средний уровень ряда динамики; средний абсолютный прирост; средний темп роста и средний темп прироста

Алгоритм 1.2. Расчёт средних показателей ряда динамики

1. В ячейке, выделенной для значения средний уровень ряда динамики (E34), перед формулой поставить знак равенства «=»;

2. Enter;

3. Выполнить действия 1–2 поочередно для всех средних показателей ряда динамики табл.3.3:

среднего абсолютного прироста;

среднего темпа роста;

Результат работы алгоритма 1.2 для демонстрационного примера приведены в табл. 3.3–ДП.

	A	B	C	D
	Таблица 3.3-ДП
	Средние показатели ряда динамики
	Средний уровень ряда динамики, млн. руб.,	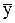3550,33
	Средний абсолютный прирост,млн. руб.,	211,40
	Средний темп роста,%,	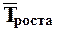106,2
	Средний темп прироста%,	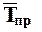6,2

Задание 2.

Прогноз показателя выпуска продукции на 7-ой год методом экстраполяции.

Выполнение Задания 2 заключается в решении двух задач:

Задача 1. Прогнозирование выпуска продукции предприятием на год вперёд с использованием среднего абсолютного прироста и среднего темпа роста.

Задача 2. Прогнозирование выпуска продукции предприятием на год вперёд с использованием аналитического выравнивания ряда динамики по прямой, параболе и полиному 3-го порядка.

Алгоритмы выполнения Задания 2

Задача 1. Прогнозирование выпуска продукции предприятием на год вперёд с использованием среднего абсолютного прироста и среднего темпа роста.

Алгоритм 2.1. Расчёт выпуска продукции на год вперёд с использованием среднего абсолютного прироста и среднего темпа роста

1. В ячейке, выделенной для значений прогнозируемого выпуска продукции по среднему абсолютному приросту (Е41), перед формулой поставить знак равенства «=».

2. Enter;

3. Выполнить действия 1–2 для прогнозируемого выпуска продукции по значению среднего темпа роста (табл.3.4).

Результат работы алгоритма 2.1 для демонстрационного примера приведен в табл. 3.4 – ДП.

	A	B	C	D	E
	Таблица 3.4–ДП
	Прогноз выпуска продукции на год вперед
	По среднему абсолютному приросту,млн. руб.,	4288,40
	По среднему темпу роста,%,	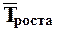4329,77

Задача 2. Прогнозирование выпуска продукции предприятием на год вперёд с использованием аналитического выравнивания ряда динамики по прямой, параболе и полиному 3-го порядка.

Алгоритм 2.2. Построение графика динамикивыпуска продукции за 6 лет с использованием средств инструмента МАСТЕР ДИАГРАММ

1. Выделить мышью ячейки, содержащие выпуск продукции за 6 лет ( диапазон ячеек B7:B12);

2. Вставка=>Диаграмма=>Точечная;

3. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4) выбрать вид точечной диаграммы, на которой значения соединены отрезками;

4. Далее;

5. В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4) выбрать вкладку Ряд и задать имя ряда 1 – «Исходные данные»;

6. Далее;

7. В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4) выбрать вкладку Заголовки и задать названия диаграммы («Прогнозирование выпуска продукции на 7-ой год») и осей Х (« Годы» ) и У ( «Выпуск продукции. млн. руб.»;;

8. Готово;

9. Выделить на полученной диаграмме ось Y (подвести курсор к требуемой оси и щелкнуть левой клавишей мыши);

10. Формат => Выделенная ось;

11. В появившемся диалоговом окне Формат оси выбрать вкладку Шкала;

12. В поле Минимальное значение – ввести минимальное (или несколько ниже) значение признака «Выпуск продукции»;

Дата добавления: 2015-03-31