Концепция риска и методы его оценки

Тема 10. РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ

1. Концепция риска и методы его оценки

2. Риск инвестиционного портфеля

3. Модель оценки доходности финансовых активов

Риск и доходность в финансовом менеджменте рассматриваются как две взаимосвязанные категории, Они могут быть ассоциированы как с каким-либо отдельным видом финансовых активов, так и с их комбинацией (в дальнейшем под активами мы будем подразумевать в основном такие финансовые инструменты, как акции и облигации).

Существуют различные определения понятия риск. Так, в наибо­лее общем виде под риском понимают вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. Можно сформулировать и более детализированные под­ходы к определению этого понятия. В частности, риск может быть определен как уровень финансовой потери, выражающейся в: а) воз­можности не достичь поставленной цели; б) неопределенности про­гнозируемого результата; в) субъективности оценки прогнозируемого результата.

Риск является весьма сложной и многоаспектной категорией. Не случайно в научной литературе приводятся десятки видов риска (про­изводственный, валютный, инвестиционный, экологический, поли­тический и др. — мы специально перечисляем разнородные виды риска, чтобы подчеркнуть их многообразие), при этом основным клас­сификационным признаком чаще всего является объект, рисковость которого пытаются охарактеризовать и проанализировать. В данной главе мы будем рассматривать риск в отношении финансовых акти­вов; кроме того, позднее будут рассмотрены другие виды риска в от­ношении управления структурой капитала компании и управления ин­вестиционными проектами.

В приложении к финансовым активам используют следующую ин­терпретацию риска и его меры: рисковость актива характеризуется сте­пенью вариабельности дохода (или доходности), который может быть получен благодаря владению данным активом. Так, государственные ценные бумаги обладают относительно небольшим риском, поскольку вариация дохода по ним в стабильной, не подверженной кризисам эко­номике практически равна нулю. Напротив, обыкновенная акция лю­бой компании представляет собой значительно более рисковый актив. поскольку доход по такого рода акциям может ощутимо варьировать.

Активы, с которыми ассоциируется относительно больший размер возможных потерь, рассматриваются как более рисковые; вполне ес­тественно, что к таким активам предъявляются и большие требования в отношении доходности.

Доход, обеспечиваемый каким-либо активом, состоит из двух ком­понентов — полученных дивидендов и дохода от изменения стоимо­сти актива. Доход, исчисленный в процентах к первоначальной стоимости актива, называется доходностью данного актива, или нормой прибыли. Доход — это абсолютный показатель, его можно суммиро­вать в пространстве и времени (в данном случае пока не учитывается временная стоимость денег); доходность — показатель относитель­ный и такого суммирования делать уже нельзя.

Пример

Предприниматель год назад приобрел акцию предприятия по цене 15 руб. Текущая рыночная цена акции — 16,7 руб., полученные дивиденды составили 1 руб. Тогда суммарный доход равен 2,7 руб., а общая доходность данного вида активов для предпринимателя составляет:

к = (1 +(16,7- 15,0))/ 15,0 = 0,18, или 18%.

Финансовые менеджеры, по возможности, пытаются учитывать риск в своей работе. При этом появляются различные варианты пове­дения, а значит, и типы менеджера в зависимости от склонности к риску. Однако ключевая идея, которой руководствуется менеджер, зак­лючается в следующем: требуемая (или ожидаемая) доходность и риск изменяются в одном направлении, т.е. пропорционально друг другу.

Совершенно очевидно, что, поскольку риск является вероятност­ной оценкой, его количественное измерение не может быть однознач­ным и предопределенным. Более того, проблема оценки риска финан­совых активов многоаспектна как с позиции методов оценки, так и с позиции стратегии и тактики управления этими активами.

Количественно риск может быть охарактеризован как некий пока­затель, измеряющий вариабельность дохода или доходности. Таким образом, первый и очевидный вывод состоит в том, что, как показано в курсе экономической статистики, для этой цели можно использо­вать ряд статистических коэффициентов, в частности: размах вариа­ции, дисперсию, среднее квадратическое отклонение, называемое иног­да стандартным, и коэффициент вариации. Дадим краткую характери­стику этим показателям, имея в виду, что в случае необходимости читатель может найти более подробную

информацию по этому воп­росу в любом стандартном учебнике по общей теории статистики.

Рассмотрим ряд статистических величин (это могут быть как абсо­лютные, так и относительные величины): x1, x2, x3,…., xn.

Размахом вариации называется разность между максимальным и минимальным значениями признака данного ряда:

R= x max – x min

Этот показатель имеет много недостатков, выделим без коммента­риев лишь три из них. Во-первых, он дает грубую оценку степени ва­риации значений признака. Во-вторых, он является абсолютным по­казателем и потому его применение в сравнительном анализе весьма ограниченно. В-третьих, его величина слишком зависит от крайних значений ранжированного ряда.

Дисперсия является средним квадратом отклонений значений при­знака от его средней и рассчитывается по формуле

Среднее квадратическое отклонение показывает среднее отклоне­ние значений варьирующего признака относительно центра распре­деления, в данном случае средней арифметической. Этот показатель рассчитывается по формуле

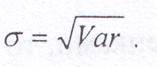(9.3)

Все вышеприведенные показатели обладают одним общим недо­статком — это абсолютные показатели, значение которых существен­но зависит от абсолютных значений исходного признака ряда. Поэто­му большее применение имеет коэффициент вариации, рассчитывае­мый по формуле

(9.4)

В отношении оценки риска финансовых активов необходимо сде­лать три замечания. Во-первых, как отмечалось выше, количественно риск может оцениваться вариабельностью либо дохода, либо доход­ности. Поскольку доход в абсолютной оценке может существенно ва­рьировать при сравнительном анализе различных финансовых акти­вов, то принято в качестве базисного показателя, характеризующего результативность операции с финансовым активом, использовать не доход, а доходность. Очевидно, что, вложив ту или иною сумму де­нежных средств в акции, можно получать разный доход по абсолют­ной величине, однако доходность не зависит от размера инвестиции и потому сопоставима в пространственно-временном разрезе.

Во-вторых, основными показателями оценки риска на рынке ка­питала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.е. отно­сительный показатель, сопоставимый как в динамике, так и по раз­личным видам активов. Поэтому независимо от анализируемых ак­тивов соответствующие им показатели доходности и дисперсии однопорядковы, и нет острой необходимости применять в оценке коэффициент вариации.

В-третьих, приведенные формулы рассчитаны на дискретные ряды, В приложении к финансовым активам они могут применяться в рет­роспективном анализе. Однако, как уже неоднократно подчеркивалось, при работе на рынке капитала гораздо более ценен перспективный анализ, в рамках которого большинство величин, представляющих интерес для инвестора, оценивается в вероятностных терминах, Имен­но поэтому при оценке риска используют модификации формул (9.2) и (9.3), в которых весами значений ожидаемой (или требуемой) доход­ности являются вероятности их появления. Ниже будут приведены соответствующие формулы для расчета.

Необходимо отметить еще одну очень важную особенность анали­за риска и доходности. Как и любая вероятностная категория, риск может быть оценен по-разному Однако речь должна идти не только и не столько о различии в алгоритмах и критериях оценки, приведен­ных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов. Эта про­блема будет рассмотрена в следующем разделе.

При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одной из рассмотренных выше статистик. Тем не менее, как и в любом перспективном анализе, инвестор в этом случае сталкивается с одной проблемой, а именно с проблемой оценки ожидаемых значений исходных параметров. В частности, какой бы мерой инвестор ни пользовался, ему необхо­димо оценить ожидаемую доходность актива. Чаще всего делают три оценки: пессимистическую (к_р), наиболее вероятную (k_{m l}) и оптими­стическую (к₀). Безусловно, число исходов может быть увеличено, однако степень разумной достоверности ожидаемых значений до­ходности и вероятностей их осуществления при этом, естественно, снизится.

Если ограничиваются тремя оценками, то наиболее общей мерой риска, ассоциируемого с данным активом, может служить размах ва­риации ожидаемой доходности, рассчитываемый по формуле

Пример

Предпринимателю необходимо выбрать лучший из двух альтернативных финансовых активов, если имеются следующие их характери­стики:

Показатель	Вариант А	Вариант Б
Цена ценной бумаги, руб.
Доходность (экспертной оценки),%:
пессимистическая
наиболее вероятная
оптимистическая
Размах вариации доходности, %

Из представленных расчетов видно, что оба финансовых актива имеют примерно одинаковую наиболее вероятную доходность, одна­ко второй из них может считаться в два раза более рисковым. Отме­тим, что, если бы был выбран какой-то другой критерий оценки рис­ка, его степень могла бы быть другой.

Можно рассчитать и другие меры риска, основанные на построе­нии вероятностного распределения значений доходности и исчисле­нии стандартного отклонения от средней доходности и коэффициента вариации, которые и рассматриваются как степень риска, ассоцииру­емого с данным активом. Таким образом, чем выше коэффициент ва­риации, тем более рисковым является данный вид актива. Последова­тельность аналитических процедур в этом случае такова:

делаются прогнозные оценки значений доходности (ki) и вероят­ностей их осуществления (pi), i = 1,... п, где п — число исходов;

рассчитывается наиболее вероятная доходность (k_ml) по формуле

рассчитывается стандартное отклонение ( с) по формуле

рассчитывается коэффициент вариации (V) по формуле

Пример

Вусловиях предыдущего примера оценить риск каждого из альтер­нативных финансовых инструментов, еслив обоих случаях вероят­ность наиболее вероятнойдоходности составляет 60%, а вероятности пессимистической и оптимистической оценок равны и составляют 20%.

Вариант A

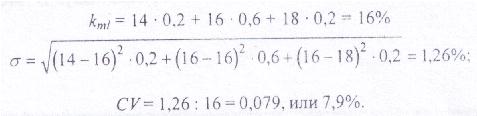
Вариант В:

Таким образом, вариант В является более рискованным по сравне­нию с вариантом А. Вместе с тем уже нельзя сказать, что он более рискован в два раза.

Приведенные рассуждения и вычислительные процедуры можно также проиллюстрировать графически. В случае с дискретным рас­пределением может быть построена столбиковая диаграмма (рис. 9.1).

Пример

Построить столбиковую диаграмму, если имеются следующие дан­ные о доходности двух активов:

Приведенные в таблице показатели вариации (расчеты, выпол­ненные по рассмотренным выше формулам, опущены) показывают, что по всем характеристикам актив А менее рискован. Соответству­ющие диаграммы представлены на рис. 9.1. Из графиков видно, что оба актива имеют одинаковую ожидаемую доходность, однако рассе­яние возможных значений доходности для актива В существенно выше, т.е. этот актив более рисков по сравнению с активом А.

Может рассматриваться и более общий случай, когда предпола­гается, что значения доходности подчинены одному из известных законов распределения, чаще всего нормальному. В этом случае вместо столбиковых диаграмм строят кривые плотности распределе­ния вероятностей f. В частности, сравнение графиков на рис. 9.2 позволяет сделать вывод, что актив В является более рисковым — соответствующий ему график более растянут вдоль оси абсцисс.

Рис.Графики кривых распределения

Риск, ассоциируемый с данным активом, как правило, рассматри­вают во времени. Очевидно, чем дальше горизонт планирования, тем труднее предсказать доходность актива, т.е. размах вариации доходно­сти, равно как и коэффициент вариации, увеличивается. Графически это можно представить следующим образом (рис. 9.3).

Рис. Риск как функция времени

Строго говоря, с удалением горизонта планирования происходит не только рост вариации, но и смещение графика вверх по оси орди­нат, т.е. в сторону увеличения требуемой доходности.

Таким образом, с течением времени риск, ассоциируемый с дан­ным активом, возрастает. Отсюда можно сделать очень важный вы­вод: чем более долговременным является данный вид актива, тем он более рискован, тем большая вариация доходности с ним связана. Именно поэтому различаются доходность и рисковость различных фи­нансовых инструментов, например акций и облигаций: вариация до­ходности акций может ощутимо варьировать, т.е. этот вид финансо­вого инструмента более рискован.

1. Риск инвестиционного портфеля

Принимая решение о целесообразности инвестирования денежных средств в финансовые активы, инвестор должен прежде всего оце­нить риск, присущий этим активам, затем ожидаемую их доходность и далее определить, достаточна ли эта доходность для компенсации ожи­даемого риска, Чаще всего инвестор работает не с отдельным акти­вом, а с некоторым их набором, называемым портфелем ценных бу­маг, или инвестиционным портфелем. Отсюда с очевидностью выте­кает, что, оценивая риск конкретного актива из инвестиционного портфеля, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой час­тью портфеля. Оказывается, что оценки рисковости актива и целесо­образности операции с ним при этом могут меняться. Более того, ак­тив, имеющий высокий уровень риска при рассмотрении его изоли­рованно, может оказаться практически безрисковым с позиции портфеля и при определенном сочетании входящих в этот портфель активов. Например, теоретически можно подобрать два финансовых актива, каждый из которых имеет высокий уровень риска, но которые, будучи объединенными, вместе составят абсолютно безрисковый пор­тфель; ниже будет рассмотрена такая ситуация. Кроме того, увеличе­ние числа включаемых в портфель активов, как правило, приводит к снижению риска данного портфеля.

Итак, риск актива — величина непостоянная и зависит, в частно­сти, от того, в каком контексте рассматривается данный актив: изоли­рованно или как составная часть инвестиционного портфеля. В пер­вом случае релевантным является общий риск актива, который коли­чественно измеряется, например, дисперсией возможных исходов относительно ожидаемой его доходности. Во втором случае релеван­тным является уже рыночный риск актива, представляющий собой долю риска данного актива в риске портфеля в целом. Разницу между этими двумя понятиями можно наглядно представить с помощью сле­дующего примера.

Предположим, что менеджер портфеля выбрал в качестве характе­ристики риска финансового актива среднее квадратическое отклоне­ние доходности и установил для себя некоторое критическое его зна­чение. Если анализируется некий актив и его риск превышает уста­новленный норматив, то он, несомненно, должен быть отвергнут.

После того как валютные средства выделены, приступают к фор­мированию инвестиционного портфеля. Арсенал методов формиро­вания портфеля достаточно обширен; наибольшим авторитетом в на­стоящее время пользуется теория инвестиционного портфеля Уилья­ма Шарпа {W.Sharpe) и Гарри Марковица (H.Markowitz). Основные принципы, изложенные в этой теории, следующие.

Во-первых, успех инвестиций в основном зависит от правиль­ного распределения средств по типам активов. Проведенные за­падными специалистами эксперименты показали, что прибыль определяется:

- на 94% выбором типа используемых инвестиционных инстру­ментов (акции крупных компаний, краткосрочные казначейские век­селя, долгосрочные облигации и др.);

• на 4% выбором конкретных ценных бумаг заданного типа;

• на 2% оценкой момента закупки ценных бумаг.

Данный феномен объясняется тем, что бумаги одного типа сильно коррелируют, т.е. если какая-то отрасль испытывает спад, то убыток инвестора не очень зависит от того, преобладают в его портфеле бу­маги той или иной компании.

Во-вторых, риск инвестиций в определенный тип ценных бумаг определяется вероятностью отклонения прибыли от ожидаемого зна­чения. Прогнозируемое значение прибыли можно определить на ос­нове обработки статистических данных о динамике прибыли от инве­стиций в эти бумаги в прошлом, а риск — как среднеквадратическое отклонение от ожидаемой прибыли.

В-третьих, общая доходность и риск инвестиционного портфеля могут меняться путем варьирования его структурой. Существуют раз­личные программы, позволяющие конструировать желаемую пропор­цию активов различных типов, например минимизирующую риск при заданном уровне ожидаемой прибыли или максимизирующую при­быль при заданном уровне риска и др.

В-четвертых, все оценки, используемые при составлении инвес­тиционного портфеля, носят вероятностный характер. Конструирова­ние портфеля в соответствии с требованиями классической теории воз­можно лишь при наличии ряда факторов: сформировавшегося рынка ценных бумаг, определенного периода его функционирования, стати­стики рынка и др.

Формирование инвестиционного портфеля осуществляется в не­сколько этапов:

• формулирование целей его создания и определение их приори­тетности в частности, что важнее — регулярное получение дивиден­дов или рост стоимости активов, задание уровней риска, минималь­ной прибыли, отклонения от ожидаемой прибыли и т.п;

• выбор финансовой компании (это может быть отечественная или зарубежная фирма; при принятии решения можно использовать ряд критериев: репутацию фирмы, ее доступность, виды предлагаемых фирмой портфелей, их доходность, виды используемых инвестицион­ных инструментов и т.п.);

• выбор банка, который будет вести инвестиционный счет.

В условиях развитого рынка ценных бумаг формирование портфе­ля и управление им представляет достаточно сложный процесс; не случайно услуги специалистов по управлению портфельными инвес­тициями оцениваются весьма высоко. Крупные компании обычно имеют отдельное подразделение по портфельным инвестициям, в рам­ках которого формируется несколько портфелей в зависимости от со­става включенных в них активов.

Одним из важнейших понятий в теории портфельных инвестиций является понятие " эффективный портфель " под которым понимает­ся портфель, обеспечивающий максимальную ожидаемую доходность при некотором заданном уровне риска или минимальный риск при заданном уровне доходности. Алгоритм определения множества эф­фективных портфелей был разработан Г.Марковицем в 50-е годы как составная часть теории портфеля. Сделанные им разработки были на­столько фундаментальными, что, по свидетельству известных специа­листов в области портфельных инвестиций Э.Элтона и М.Грубера, исследования в этой области в последующие сорок лет сводились в основном к разработке методов применения базовых идей и концеп­ций теории Марковица [Elton, Gruber, с.97].

Очевидно, что эффективных портфелей может быть построено много, поэтому вводится понятие «оптимальный портфель». Ос­новная идея определения оптимального портфеля в рамках теории Марковица может быть описана следующим образом. Инвестор строит для себя набор кривых безразличия, т.е. кривых, отражающих раз­личные комбинации доходности и риска. Считается, что чем выше расположена кривая, тем выше и уровень удовлетворенности, дости­гаемый инвестором.

Все комбинации, находящиеся на некоторой кривой безразличия, равноприемлемы для инвестора, т.е. он безразличен к выбору конк­ретной комбинации из набора. Далее строится набор эффективных портфелей (имеется в виду, что если инвестор имеет на выбор два портфеля одинакового риска, но с разной доходностью, то портфель, имеющий большую доходность, и будет эффективным). Оптималь­ным для инвестора будет портфель, характеризующийся точкой пере­сечения множества эффективных портфелей и одной из кривых без­различия.

Дата добавления: 2015-03-31