
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность
|
|
|
|
Помните, что на самом деле никто на свете не одинок. Просто, может быть, вы до сих пор не встречали тех, кто мыслит, чувствует, думает родственно с вами. Но если по этому пути идете вы — то обязательно рядом есть кто-то еще. Пусть счастливые встречи на Пути состоятся поскорее. Пусть с вами будут добро и щедрость души. Дарите радость людям и миру.
Заключение
Вот вы и познакомились с новым пособием. Спасибо вам, мои дорогие читатели, за то, что вы есть, что вы стремитесь вдаль, к горизонтам Вселенной.
Вам уже не нужно говорить о преимуществах той жизни, которую мы для себя открываем. Скука и серое прозябание обыденности остались далеко позади. Гражданин Вселенной не разменивает мгновения бытия на мелочные переживания, пустые хлопоты и мышиную возню вокруг мнимых ценностей — будь то деньги, власть или погоня за роскошью. Вы сами себе — целый мир, творимый и созидаемый ежесекундно, вы сами себе и творец, строящий себя и свою жизнь по иным, высоким законам. Сколько красоты в нашей жизни, в созидании, в сиянии зажженной звезды, втом высоком и прекрасном измерении, в котором мы все существуем! Человек поистине высок духом, свободен и прекрасен. Поистине человеку нет границ.
Мы с вами о многом еще не говорили — мы не говорили о структуре человеческого сознания, о его взаимодействии с коллективным бессознательным. Мы не говорили о других мирах, доступных человечеству, о возможности контактов с ближними и дальними мирами, о переселении сознания на иные носители, о том, что миры многослойны… У нас еще впереди множество тем для бесед, размышлений, практического освоения. Им будет посвящена следующая, завершающая цикл книга. А потому мы с вами не прощаемся. Нас ждет новая встреча.
Силы, творчества и счастья вам!
Спасибо, что скачали книгу в бесплатной электронной библиотеке ModernLib.Ru
Все книги автора
Эта же книга в других форматах
6. Функция  . Свойства и график.
. Свойства и график.
7. Функция  . Свойства и график.
. Свойства и график.
8. Функция 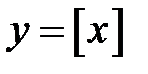 . Свойства и график.
. Свойства и график.
9. Функция  . Свойства и график.
. Свойства и график.
10. Функция  . Свойства и график.
. Свойства и график.
НОМЕРА 6-10 ПО ПЛАНУ ДЕЛАТЬ. ПРОСТО ОПИСАТЬ ЕЕ И НАЧЕРТИТЬ.
11. Понятие сложной функции. Привести примеры.
Сложная функция - функция, представленная как композиция нескольких функций.
Пример: SQRT(x^2+4x)
12. Определение чётной и нечётной функций. Привести примеры.
Если f(x)=f(-x) - четная
f(-x)=-f(x) – нечетная
13. Теоремы о графиках чётной и нечетной функции. Привести примеры.
Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
Индифферентная функция — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.
· Функция 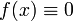 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной.
· Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
· Функция, обратная чётной, чётна, а нечётной — нечётна.
· Произведение двух функций одной чётности чётно.
· Произведение двух функций разной чётности нечётно.
· Композиция двух нечётных функций нечётна.
· Композиция чётной функции с чётной/нечётной чётна.
· Композиция любой функции с чётной чётна (но не наоборот!).
14. Определение функции, ограниченной сверху (снизу). Привести примеры.
Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D.
15. Определение функции, ограниченной на множестве 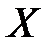 . Привести примеры.
. Привести примеры.
Игрек=Икс в квадрате ограничена снизу
Игрек равно корень из икс ограничена снизу
16. Определение функции, возрастающей (убывающей) на множестве 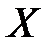 . Привести примеры.
. Привести примеры.
Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает на множестве Х, если большему значению аргумента х соответствует большее значение функции у. Функция убывает на множестве Х, если большему значению аргумента х соответствует меньшее значение функции у.
17. Перечислить свойства монотонных функций. Привести примеры. Доказать одно из свойств.
В учебнике есть. В самом начале. И примеры и док-ва
18. Наибольшее и наименьшее значение функции на множестве 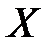 . Привести примеры.
. Привести примеры.
ЭКСТРЕМУМ ФУНКЦИИ — термин, объединяющий понятия максимума и минимума функции.
Точку х0 называют точкой локального максимума, если у нее существует окрестность, для всех точек которой (кроме х0) выполняется неравенство f(x)<f(x0)
Для минимума наоборот.
19. Преобразования графика функции: 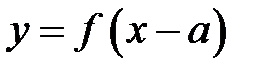 и.
и.  . Привести примеры.
. Привести примеры.
20. Преобразования графика функции:  и
и  . Привести примеры.
. Привести примеры.
21. Преобразования графика функции:  и
и 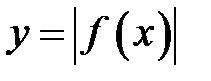 . Привести примеры.
. Привести примеры.
22. Преобразования графика функции:  и
и 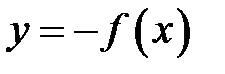 Привести примеры.
Привести примеры.
23. Функции у = ах2, у = ах2 + n и у = а(х - т)2. Свойства и график.
Все преобразования есть в учебнике. И там вообще очень просто.
24. Целое уравнение и его корни. Теорема Безу. Теорема о целых корнях многочлена с целыми коэффициентами.
25.
26. Числовые последовательности. Способы задания последовательностей. Возрастающие и убывающие последовательности.
Последовательность – набор чисел, каждое из которых снабжено своим номером
Задание: Аналитически (формулой), Словесно – последовательность простых чисел.
Пусть имеется множество  , на котором введено отношение порядка.
, на котором введено отношение порядка.
Последовательность 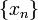 элементов множества
элементов множества  называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
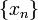 — неубывающая
— неубывающая 
Последовательность 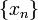 элементов множества
элементов множества  называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
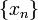 — невозрастающая
— невозрастающая 
Последовательность 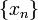 элементов множества
элементов множества  называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
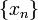 — возрастающая
— возрастающая 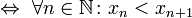
Последовательность 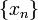 элементов множества
элементов множества  называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
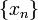 — убывающая
— убывающая 
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.
Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.
27. Числовые последовательности. Способы задания последовательностей. Ограниченные и неограниченные последовательности.
Ограниченная сверху последовательность — это последовательность элементов множества  , все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.
 ограниченная сверху
ограниченная сверху 
Ограниченная снизу последовательность — это последовательность элементов множества  , для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.
 ограниченная снизу
ограниченная снизу 
Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.
 ограниченная
ограниченная 
Неограниченная последовательность — это последовательность, которая не является ограниченной.
 неограниченная
неограниченная 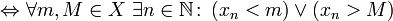
28. Арифметическая прогрессия. Формула n-го члена арифметической прогрессии.
Арифмети́ческая прогре́ссия — числовая последовательность вида
 ,
,
то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа  (шага или разности прогрессии):
(шага или разности прогрессии):
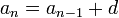
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
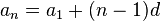
Арифметическая прогрессия является монотонной последовательностью. При 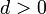 она является возрастающей, а при
она является возрастающей, а при 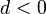 — убывающей. Если
— убывающей. Если  , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения 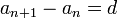 для членов арифметической прогрессии.
для членов арифметической прогрессии.
Сумма первых 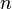 членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам
 , где
, где 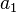 — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером 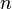 ,
, 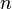 — количество суммируемых членов.
— количество суммируемых членов.
 , где
, где 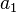 — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии, 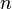 — количество суммируемых членов.
— количество суммируемых членов.
29. Сумма первых п членов арифметической прогрессии
Сумма первых 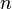 членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам
 , где
, где 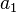 — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером 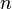 ,
, 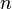 — количество суммируемых членов.
— количество суммируемых членов.
 , где
, где 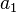 — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии, 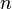 — количество суммируемых членов.
— количество суммируемых членов.
30. Геометрическая прогрессия. Формула n -го члена геометрической прогрессии.
Геометри́ческая прогре́ссия — последовательность чисел 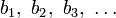 (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число  (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
,  :
: 
Любой член геометрической прогрессии может быть вычислен по формуле:

Если  и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если 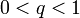 , — убывающей последовательностью, а при
, — убывающей последовательностью, а при 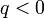 — знакочередующейся
— знакочередующейся
Своё название прогрессия получила по своему характеристическому свойству:
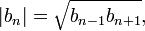
то есть каждый член равен среднему геометрическому его соседей.
31. Сумма первых n членов геометрической прогрессии.
Любой член геометрической прогрессии может быть вычислен по формуле:

Если  и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если 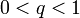 , — убывающей последовательностью, а при
, — убывающей последовательностью, а при 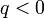 — знакочередующейся
— знакочередующейся
Своё название прогрессия получила по своему характеристическому свойству:
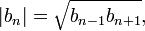
то есть каждый член равен среднему геометрическому его соседей.
32. Характеристические свойства арифметической и геометрической прогрессий.
Просто перечислить главное из ранее написанного.
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 1508; Нарушение авторских прав?; Мы поможем в написании вашей работы!