Образцы решения типовых задач контрольной работы

I задание. В библиотеке имеется 20 учебников по высшей математике, из которых 5 рекомендуются для студентов агрономического факультета. Какова вероятность того, что из трех взятых студентом учебников два окажутся рекомендованными для студентов агрономического факультета?

Решение. Введем обозначения событий: A – «из трех взятых учебников два рекомендованы для студентов агрономического факультета».

Общее число возможных элементарных исходов испытания равно число способов, которыми можно взять три учебника из двадцати возможных, т.е. числу сочетаний из 20 элементов по 3 .

Определим число исходов, благоприятствующих событию А. Два учебника из пяти, рекомендованных для студентов агрономического факультета, можно взять способами; при этом оставшийся 3-2=1 учебник должен входить в список учебников, не рекомендованных для студентов агрономического факультета. Взять этот учебник из 20-5=15 учебников можно 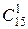=15 способами. Следовательно, число благоприятствующих исходов равно .

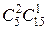Схематично представить описанное выше решение можно в виде рисунка 1.

Рисунок 1

Таким образом, по классическому определению вероятности имеем: .

Вычислим отдельные множители, входящие в , пользуясь формулой ;

;

;

.

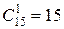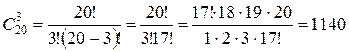В итоге получим: .

II задание. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках, равны 0,6; 0,7 и 0,8 соответственно. Найти вероятности того, что формула содержится:

А) только в одном справочнике;

Б) только в двух справочниках;

В) во всех трех справочниках;

Г) хотя бы в одном справочнике.

Решение. Введем необходимые для решения события:

А ₁ – «формула содержится в первом справочнике»;

А ₂– «формула содержится во втором справочнике»;

А ₃ – «формула содержится в третьем справочнике».

Заметим, что вероятность отыскать формулу в каком-либо справочнике не зависит от вероятности обнаружить эту формулу в других справочниках (события А _1, А _2, А ₃ независимы).

По условию 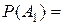0,6, 0,7, 0,8.

Вероятности событий, противоположных событиям А _1, А _2, А _3, соответственно равны:

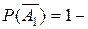
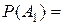1-0,6=0,4;

1-0,7=0,3;

1-0,8=0,2.

Воспользуемся теоремами сложения и умножения вероятностей.

А) Пусть А – «формула содержится только в одном справочнике»; это значит, что формула может содержаться:

- в первом справочнике, но во втором и третьем не содержаться ;

- во втором справочнике, но в первом и третьем не содержаться ;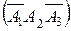

- в третьем справочнике, но в первом и втором не содержаться .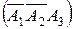

Поэтому .

Поскольку события , , несовместны, то применима теорема сложения:

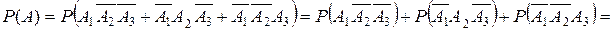=0,6×0,3×0,2+0,4×0,7×0,2+0,4×0,3×0,8=0,188.

Б) Пусть В – «формула содержится только в двух справочниках»; это значит, что формула может содержаться:

- в первом и втором справочниках, но в третьем не содержаться ;

- в первом и третьем справочниках, но во втором не содержаться ;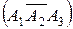

- во втором и третьем справочниках, но в первом не содержаться .

Поэтому .

Поскольку события 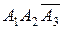, , 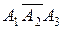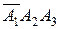несовместны, то применима теорема сложения:

=0,6×0,7×0,2+0,6×0,3×0,8+0,4×0,7×0,8=0,452.

В) Пусть С – «формула содержится во всех трех справочниках», следовательно:

=0,6×0,7×0,8=0,336.

Г) Пусть D – «формула содержится хоты бы в одном справочнике».

Искомая вероятность равна:

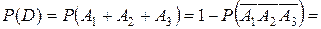1-0,4×0,3×0,2=0,976.

III задание. Трое рабочих цеха обслуживают станки. Первый рабочий обслуживает 20 станков, второй – 30 станков, третий – 50 станков. Вероятность того, что станки, обслуживаемые первым рабочим, в течение смены безотказно работают, равна 0,9, для второго и третьего рабочих эта вероятность равна, соответственно, 0,8, 0,7. А) Какова вероятность того, что выбранный наудачу станок цеха безотказно проработает в течение смены? Б) Станок цеха, выбранный наудачу, безотказно проработал в течение смены. Какова вероятность того, что этот станок обслуживается вторым рабочим?

Решение. Введем необходимые для решения задачи события: А – «выбранный наудачу станок цеха безотказно проработает в течение смены», гипотезы H_i – «станок обслуживается i -м рабочим» (i =1,2,3). Вероятности гипотез находим по классическому определению вероятности:

, , ;

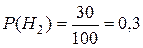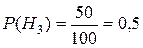условие 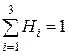выполняется.

А) Вероятность того, чтовыбранный наудачу станок цеха безотказно проработает в течение смены, находим по формуле полной вероятности:

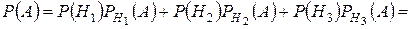
= 0,77.

Б) Если станок цеха, выбранный наудачу, безотказно проработал в течение смены, то вероятность того, что этот станок обслуживается вторым рабочим, найдем по формуле Байеса:

.

IV задание. Вероятность получения в лотерее выигрышного билета равна 0,1. Какова вероятность того, что среди 400 наугад купленных билетов выигрышных: А) 40; Б) не менее 50 и не более 60?

Решение. А) Вычислить искомую вероятность 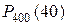по формуле Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим приближенную формулу локальной теоремы Лапласа:

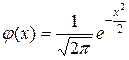, где и .

По условию задачи p =0,1; q =1-0,1=0,9; n =400; k =40. Тогда . Из таблицы приложения 1 находим 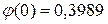. Искомая вероятность равна 0,0665.

Б) Вычислим искомую вероятность 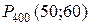, используя интегральную теорему Лапласа:

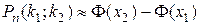, где и 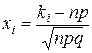(i =1, 2).

По условию задачи p =0,1; q =1-0,1=0,9; n =400; k ₁=50; k ₂=60. Находим

, .

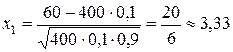Из таблицы приложения 2 находим , .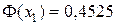

Откуда =0,047.

V задание. В хлопке число длинных волокон составляет 60%. Для исследования наудачу взяты 3 волокна. Требуется: А) найти закон распределения вероятностей дискретной случайной величины X – число длинных волокон среди взятых; Б) определить вид закона распределения случайной величины X; В) построить многоугольник распределения; г) составить функцию распределения вероятностей случайной величины и построить ее график; д) вычислить числовые характеристики X.

Решение. А) Составим закон распределения случайной величины X. Из трех взятых волокон могут иметь длинные волокна три, два, одно волокно или вообще ни одно из них не может иметь длинных волокон. Поэтому получаем таблицу возможных значений X:

xi
pi	p 0	p 1	p 2	p 3

Найдем вероятности p_i (i =1, 2, 3, 4), используя формулу Бернулли. Если производится серия n независимых испытаний, при каждом из которых вероятность наступления события постоянна и равна p, тогда вероятность того, что это событие в n испытаниях появится ровно k раз, вычисляется по формуле:

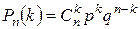, где и q =1- p.

Имеем: p =0,6, q= 1 - 0,6 = 0,4, n= 3. Тогда:

;

;

;

.

Проверим тот факт, что . Действительно, 0,064+0,288+0,432+ +0,216=1. Следовательно, закон распределения X окончательно имеет вид:

xi
pi	0,064	0,288	0,432	0,216

Б) Поскольку при нахождении вероятностей p_i была использована формула Бернулли, то указанная случайная величина имеет биномиальный закон распределения вероятностей.

В) Многоугольник распределения (рис. 2) – ломаная, звенья которой соединяют точки с координатами (i= 0,1,2,3).

Г) Функция распределения вероятностей случайной величины X определяется равенством F (x)= P (X < x). Имеем:

.

Построим график этой функции (рис. 3):

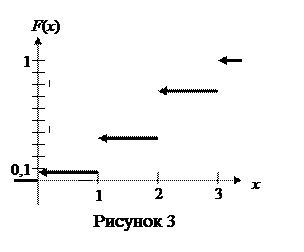
Д) Найдем числовые характеристики X.

Математическое ожидание случайной величины X определяется равенством: 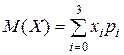. Имеем:

.

Для нахождения дисперсии составим закон распределения вероятностей случайной величины X ²:

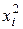
pi	0,064	0,288	0,432	0,216

Найдем математическое ожидание X ²:

.

Тогда, вычисляя дисперсию случайной величины X по формуле , получаем: .

Среднее квадратическое отклонение случайной величины X находится как . Имеем: .

VI задание. Случайная величина X задана интегральной функцией распределения вероятностей 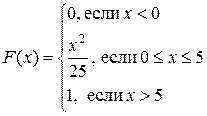. А) построить график функции F(x); Б) найти дифференциальную функцию распределения вероятностей f(x) и построить ее график; В) вычислить числовые характеристики X; Г) найти .

Решение. А) Построим график интегральной функции распределения вероятностей (рис. 4).

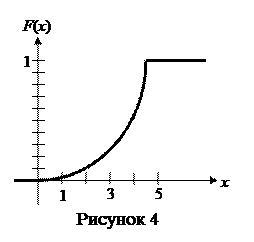
Б) Дифференциальную функцию распределения вероятностей определяем по формуле: 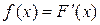. Имеем: . Построим график этой функции (рис. 5).

В) Вычислим числовые характеристики X.

Математическим ожиданием непрерывной случайной величины X называется значение интеграла , где f (x)– дифференциальная функция распределения вероятностей. В нашем случае

.

Для нахождения дисперсии непрерывной случайной величины X может быть использована формула 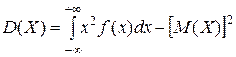, где f (x)– дифференциальная функция распределения вероятностей. Получаем:

.

Среднее квадратическое отклонение . Имеем: .

Г) Для нахождения воспользуемся формулой . Тогда искомая вероятность .

VII задание. Случайные значения веса зерна распределены нормально. Среднее значение веса зерна равно 0,2 г, среднее квадратическое отклонение равно 0,04 г. Нормальные всходы дают зерна, вес которых более 0,15 г. Определить:

А) процент семян, которые дадут нормальные всходы;

Б) границы, в которых с вероятностью 0,9973 заключен вес наудачу взятого зерна.

Решение.

А) Пусть случайная величина Х – значение веса зерна. По условию 0,2, =0,04.

Определим вероятность того, что случайно взятое зерно даст нормальные всходы, т.е. определим . Сначала найдем вероятность того, что вес зерна не превысит 0,15 г. Для этого воспользуемся формулой: . Тогда:

.

Поскольку функция 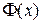нечетная, получим:

.

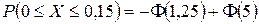Откуда по таблице приложения 2 имеем:

.

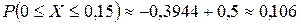Тогда =1- 1-0,106=0,894.

Таким образом, только 89,4% зерен дадут нормальные всходы.

Б) Для определения границ, в которые с вероятностью 0,9973 попадет вес случайно взятого зерна, воспользуемся правилом трех сигм:

.

Имеем: 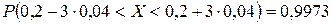, откуда .

Таким образом, вероятность того, что абсолютная величина отклонения веса зерна превысит утроенное его среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев вес зерна окажется не лежащим в диапазоне (0,08;0,32 г). Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными.

Дата добавления: 2015-03-31