
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Коррозия металлов. Защита металлов от коррозии
|
|
|
|
Коррозия металлов. Защита металлов от коррозии.
Задача 1. Подтвердить термодинамическую возможность газовой коррозии (высокотемпературного окисления) железного изделия при Т = 800 К в газовой смеси, парциальное давление кислорода в которой равняется 0,01 атм, если она сопровождается образованием на поверхности изделия оксида FeO. Вычислить парциальное давление кислорода, ниже которого коррозия прекратиться при заданной температуре, а также определить температуру, выше которой коррозия станет невозможной при стандартных состояниях компонентов.
Решение. Для подтверждения возможности газовой коррозии, описываемой уравнением
2Fe(т) + O2 (г) D 2FeO(т) 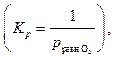
рассчитывают значение энергии Гиббса протекающего процесса при Т = 800 К. Для этого используют уравнение изотермы Вант−Гоффа, которое для рассматриваемого процесса выглядит как
Δ rG 800 = Δ rG 0800 + R ∙800∙ln 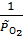 ,
,
где 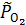 =
= 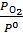 = 0,01 – относительное значение неравновесного парциального давления кислорода.
= 0,01 – относительное значение неравновесного парциального давления кислорода.
В последнем стандартную энергию Гиббса Δ rG 0800 находят по приближенной форме уравнения Гиббса−Гельмгольца:
Δ rG 0800 ≈ 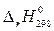 − 800·
− 800· 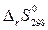
Значение 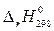 вычисляют по следствию из закона Гесса:
вычисляют по следствию из закона Гесса:
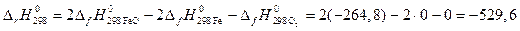 кДж.
кДж.
Аналогично по справочным величинам 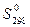 находят
находят 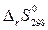 .
.
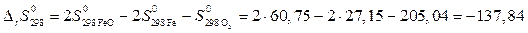 Дж/K
Дж/K
В итоге
Δ rG 0800 = −529,6 − 800·(−137,84·10−3) = −419,33 кДж
а
Δ rG 800 = −419,33 − 8,31·800·10−3·ln 0,01 = −388,70 кДж
Так как Δ rG 800 < 0, то газовая коррозия железного изделия в данных условиях термодинамически возможна. Она не будет протекать, если
Δ rG 800 = Δ rG 0800 + R ∙800∙ln 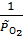 > 0,
> 0,
т.е. когда
ln 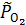 <
< 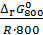 и
и
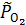 < exp(
< exp(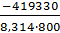 ) или
) или 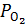 < 4,16∙10−28 атм.
< 4,16∙10−28 атм.
Температуру, выше которой коррозия будет невозможна при стандартных состояниях компонентов можно найти из неравенства
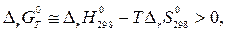
откуда, подставив конкретные значения 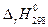 и
и 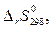 имеем, что при
имеем, что при
 K.
K.
Задача 2. Расчетами ЭДС Е 298 коррозионного элемента и энергии Гиббса Δ rG 298 коррозионного процесса подтвердите возможность электрохимической коррозии при температуре 298,15 К изделия из никеля, находящегося в деаэрированной воде с рН = 7. Предполагается, что коррозия протекает в выделение водорода и образованием Ni(OH)2, произведение растворимости которого при Т = 298,15 К составляет 1,6·10−14.
Решение. Вначале уравнениями описывают возможные электродные процессы:
(−) А: Ni → Ni2+ + 2 e
(+) K: 2H2O + 2 e → H2↑ + 2OH−
Складывая эти уравнения получают суммарное уравнение, которое описывает коррозионный процесс в целом:
Ni + 2H2O = Ni(OH)2↓ + H2↑
Далее по адаптированному для Т = 298,15 К уравнению Нернста рассчитывают потенциал анода, т.е. как видно из приведенного уравнения, никелевого электрода:
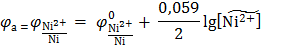
 = −0,250 В – значение стандартного потенциала никелевого электрода (справочная величина). Относительное значение концентрации ионов Ni2+ есть
= −0,250 В – значение стандартного потенциала никелевого электрода (справочная величина). Относительное значение концентрации ионов Ni2+ есть
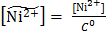 ,
,
где [Ni2+] – абсолютное значение концентрации ионов Ni2+; С 0 = 1 моль/л – значение стандартной концентрации.
[Ni2+] находят по значению 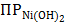 . В водном растворе малорастворимого вещества, которым является Ni(OH)2, устанавливается равновесие, описываемое следующим уравнением:
. В водном растворе малорастворимого вещества, которым является Ni(OH)2, устанавливается равновесие, описываемое следующим уравнением:
Ni(OH)2 (т) ⇄ Ni2+(р) + 2ОН−(р)
С С 2 С
По определению
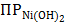 = [Ni2+]∙[OH−]2 = C∙ (2 C)2 = 4C3,
= [Ni2+]∙[OH−]2 = C∙ (2 C)2 = 4C3,
где C – молярная концентрация насыщенного водного раствора Ni(OH)2 или растворимость последнего. Видно, что
[Ni2+] = С = 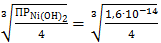 = 1,587∙10−5 моль/л
= 1,587∙10−5 моль/л
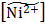 = 1,587∙10−5
= 1,587∙10−5
[OH−] = 2 C = 3,174∙10−5 моль/л.
После подстановки найденного значения в уравнение Нернста получают
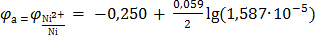 = −0,392 В.
= −0,392 В.
Из приведенного уравнения катодного процесса видно, что это уравнение водородного электрода, адоптированного для Т = 298,15 K форма уравнения Нернста для которого имеет вид
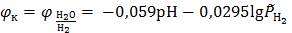 .
.
Поскольку в процессе коррозии среда (вода) подщелачивается (см. уравнение катодного процесса) и таким образом ее рН становится большим 7, то его значение находят через ионное произведение воды 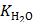 = 10−14 и рассчитанную из
= 10−14 и рассчитанную из 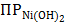 равновесную концентрацию OH− -ионов (см. выше).
равновесную концентрацию OH− -ионов (см. выше).
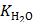 = [H+]∙[OH−]
= [H+]∙[OH−]
[H+] = 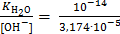 = 3,151∙10−10 моль/л или
= 3,151∙10−10 моль/л или
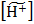 = 3,151∙10−10.
= 3,151∙10−10.
Отсюда
рН = −lg 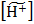 = −lg(3,151∙10−10) = 9,50.
= −lg(3,151∙10−10) = 9,50.
Относительное значение парциального давления водорода 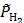 в атмосфере Земли составляет 5∙10−7. После подстановки значений рН и
в атмосфере Земли составляет 5∙10−7. После подстановки значений рН и 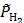 в адаптированную форму уравнения Нернста получают, что
в адаптированную форму уравнения Нернста получают, что
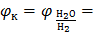 −0,059∙9,5 – 0,0295∙lg(5∙10−7) = −0,375 В.
−0,059∙9,5 – 0,0295∙lg(5∙10−7) = −0,375 В.
Далее
Е 298 = 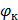 −
− 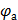 = −0,375 – (−0,392) = 0,017 В, а
= −0,375 – (−0,392) = 0,017 В, а
Δ rG 298 = − nFE = −2∙96485,3∙0,017 = −3280,50 Дж.
Так как Е 298 > 0, Δ rG 298 < 0, то коррозия изделия из никеля в данных условиях с выделением Н2 и образованием Ni(OH)2 возможна.
Задача 3. Изделие из оцинкованного железа подверглось электрохимической коррозии в водном растворе с рН = 10. При этом поглотилось 280 мл О2 и выделилось 112 мл Н2, измеренных при н.у. Приведите уравнения анодного и катодного процессов. Рассчитайте массы прокорродировавшего при этом металла и образовавшихся продуктов.
Решение. Так как φ0Zn2+/Zn = −0,763 B < φ0Fe2+/Fe = −0,440 B, то цинковое покрытие на железном изделии является анодным и защищает его электрохимически. В соответствии с механизмом защитного действия именно оно (покрытие) и будет разрушаться. Таким образом анодный процесс описывается уравнением
(−) А (Znпокр.): Zn → Zn2+ + 2 e | 3
В соответствии с условием задачи на катоде, которым является железная основа, протекают две реакции, одна с поглощением О2, т.е. с кислородной деполяризацией, другая с выделением Н2, т.е. с водородной деполяризацией

Число моль эквивалентов поглощенного О2 и выделившегося Н2 на катоде
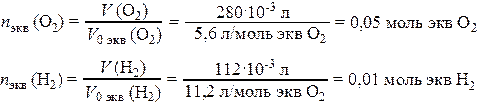
где V 0 экв (О2) и V 0 экв (Н2) – молярный объемы химических эквивалентов при н.у. кислорода и водорода соответственно. Суммарное число моль эквивалентов газов, подвергшихся превращению на катоде: n экв Σ = 0,05 + 0,01 = 0,06 моль экв. Согласно закону эквивалентов, такое же число моль эквивалентов цинка прокорродировало. Тогда
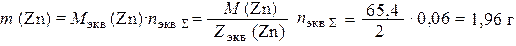
где М экв (Zn) и Z экв (Zn) – молярная масса химического эквивалента цинка и его эквивалентное число соответственно.
Складывая уравнения анодного и катодного процессов, предварительно уравняв с помощью коэффициентов 3 и 1 число отдаваемых и принимаемых электронов, получаем уравнение, описывающее коррозионный процесс:
3Zn + O2 + 4H2O = 3Zn(OH)2↓ + H2↑
Видно, что вторым продуктом коррозии является Zn(OH)2. Согласно закону эквивалентов его масса:
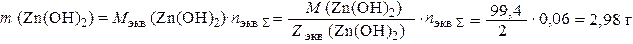
где М экв (Zn(ОН)2) и Z экв (Zn(ОН)2) – молярная масса химического эквивалента Zn(OH)2 и его эквивалентное число соответственно.
Масса выделившегося водорода составила
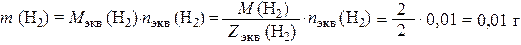
где М экв (Н2) и Z экв (Н2) – молярная масса химического эквивалента водорода и его эквивалентное число соответственно.
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 3302; Нарушение авторских прав?; Мы поможем в написании вашей работы!