Пример 6

Пример 5

Пример 4

Пример 3

Пример 2

Пример 1

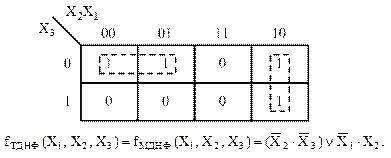
Рисунок 27 – Карта Карно и результат минимизации к примеру 1

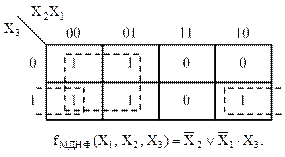
Рисунок 28 – Карта Карно и результат минимизации к примеру 2

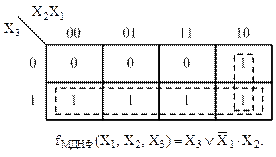
Рисунок 29 – Карта Карно и результат минимизации к примеру 3

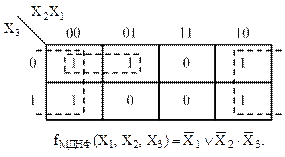
Рисунок 30 – Карта Карно и результат минимизации к примеру 4

В примерах 5 и 6 (рисунки 31-32) результат минимизации запишем в МКНФ. При этом следует помнить, что в КНФ справедливо соотношение:

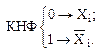(42)

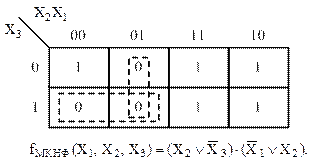
Рисунок 31 – Карта Карно и результат минимизации к примеру 5

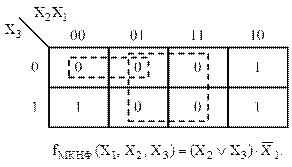
Рисунок 32 – Карта Карно и результат минимизации к примеру 6

Минимизация не полностью заданных логических функций

По условиям работы цифрового устройства некоторые наборы значений аргументов могут оказаться запрещенными для данного устройства и никогда не появиться на его входах. В этом случае функция задана не на всех наборах аргументов. Такие функции называются не полностью заданными.

При синтезе цифрового устройства, реализующего не полностью заданную функцию, допустимо задаваться произвольными значениями функции на запрещенных наборах аргументов. При этом в зависимости от способа задания этих значений функции минимальная форма может оказаться простой или более сложной. Таким образом, возникает проблема целесообразности доопределения функции на запрещенных наборах аргументов. При минимизации не полностью заданных логических функций следует на запрещенных наборах аргументов задавать функии такие значения, при которых клетки со значением 1 (либо 0) охватываются минимальным числом областей с максимальным числом клеток в каждой из областей.

На рисунке 33 показана карта Карно для не полностью заданной функции (Ф – неопределенное значение функции).

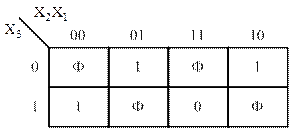
Рисунок 33 – Карта Карно для не полностью заданной логической функции

Применительно к рассматриваемой функции (рисунок 33) такое доопределение функции может быть осуществлено тремя различными способами, представленными на рисунке 34.

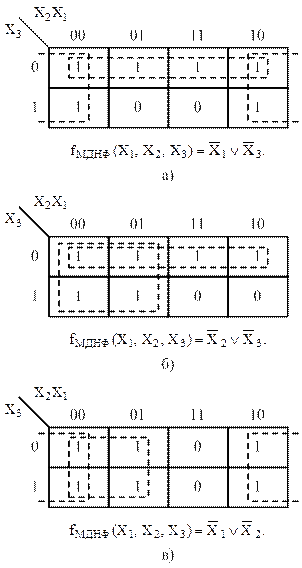
Рисунок 34 – Варианты минимизации не полностью заданной логической функции

Все три варианта минимизации дают равноценные по сложности результаты.

Примеры синтеза КЦУ, реализующего не полностью заданную логическую функцию четырех аргументов, подробно рассмотрены в [5, ч. 1].

Особенности синтеза КЦУ с несколькими выходами рассмотрены в [1].

ЛИТЕРАТУРА

1 Калабеков, Б. А. Цифровые устройства и микропроцессорные системы: учеб. для техникумов связи / Б. А. Калабеков. – М.: Горячая линия – Телеком, 2002. – 336 с.

2 Калабеков, Б. А. Цифровые устройства и микропроцессорные системы: учеб. для техникумов связи / Б. А. Калабеков, И. А. Мамзелев. – М.: Радио и связь, 1987. – 400 с.

3 Лысиков, Б. Г. Цифровая и вычислительная техника: учеб. для техникумов связи / Б. Г. Лысиков. – Мн.: УП Экоперспектива, 2002. – 264 с.

4 Угрюмов, Е. П. Цифровая схемотехника: учеб. пособие для вузов / Е. П. Угрюмов. – Спб.: БХВ-Петербург, 2002. – 582 с.

5 Цифровые и микропроцессорные устройства: лабораторный практикум для студентов специальностей 2-45 01 03 – Сети телекоммуникаций, 2‑45 01 02 – Системы радиосвязи, радиовещания и телевидения. В 4 ч. / сост. В. И. Богородов. – Минск: ВГКС, 2009. – Ч. 1 – 84 с.; Ч. 2 – 65 с.

6 Цифровые интегральные микросхемы: справочник, 2-е изд., перераб. и доп. / М. И. Богданович [и др.]. – Мн.: Беларусь, Полымя, 1996. – 605 с.

СОДЕРЖАНИЕ

Введение. 3

Арифметические основы цифровой техники. 3

Системы счисления. Основные понятия. Выбор системы счисления для цифровых устройств 3

Перевод чисел из одной позиционной системы счисления в другую 7

Представление двоичных чисел в формах с фиксированной и плавающей точкой 10

Способы кодирования двоичных чисел. 14

Арифметические операции над двоичными числами с фиксированной точкой 16

Особенности арифметических операций над двоичными числами с плавающей точкой 21

Сложение двоично-десятичных чисел. 22

Символьные коды.. 23

Структурные единицы и форматы цифровых данных. 25

Логические основы цифровой техники. 26

Понятие о логических функциях, логических элементах и логических устройствах 26

Классификация логических устройств. 28

Способы задания логических функций. 29

Элементарные логические функции одного аргумента. 30

Элементарные логические функции двух аргументов. 32

Основные законы и тождества алгебры логики. 38

Понятие базиса и минимального базиса. 41

Преобразование логических функций из основного базиса в неосновные 45

Схемотехнические основы цифровой техники. 48

Общие сведения об элементной базе цифровой техники. 48

Классификация цифровых интегральных схем.. 49

Обозначения цифровых интегральных схем.. 51

Основные статические и динамические параметры логических элементов 53

Типы выходных каскадов цифровых элементов. 59

Логический выход. 60

Выход с тремя состояниями. 62

Выход с открытым коллектором (стоком) 63

Построение узлов цифровых устройств на стандартных микросхемах 67

Схемотехника входных цепей элементов КМОП и режимы временно разомкнутых входов 70

Анализ и синтез комбинационных. 72

Цифровых устройств. 72

Этапы синтеза комбинационных цифровых устройств. 72

Канонические формы представления логических функций 73

Исходные положения к минимизации. 76

Этапы минимизации. 77

Табличный метод минимизации. 79

Минимизация не полностью заданных логических функций 85

Литература. 88

Учебное издание

Дата добавления: 2015-03-31