Интегрирующая цепь

В интегрирующей цепи конденсатор включается параллельно входу изме­рительного прибора (рис.2.18). В такой цепи напряжение на резисторе равно

U_R = U_вх – U_вых,

а ток через конденсатор соответственно равен

I=C(dU_вых/dt)=(U_вх-U_вых)/R

При большом значении произведения RC для выходного напряжения получим:

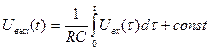2.15

Таким образом, выходное напряжение схемы будет равно интегралу по времени от входного.

Если на вход такой цепи подать прямоугольный импульс (а), то при по­стоянной времени много большей длительности импульса t_имп,, RC >> t_имп, то на выходе мы будем иметь (б) линейно нарастающее напряжение U_вых = a×t+c, которое отображает начальный участок экспоненты, являющейся решением уравнения (2.15)

Если источником сигнала является источник тока, а не источник напряже­ния, т.е. величина тока через конденсатор задана, то выходное напряжение будет строго пропорционально интегралу от тока, независимо от постоянной времени цепи. Такая ситуация реализуется, в частности, при очень высоком значении сопротивления R и соответствует идеальному интегратору сигнала.

По мере того как величина постоянной времени будет уменьшаться или, что то же самое, будет уменьшаться длительность импульса, искажения, кото­рые вносит интегрирующая цепь, уменьшаются. При RC<<t _имп сигнал проходит через интегрирующую цепь с минимальными искажениями (д).

RC - фильтры.

В цепи переменного тока дифференцирующие и интегрирующие цепи пред­ставляют собой комплексное сопротивление, состоящее из активного сопротив­ления R и емкостного сопротивления Z _C = -i/wC. Поскольку комплексное сопро­тивление (импеданс) зависит от частоты, то варьируя соотношение между ак­тивной и реактивной составляющими можно изменять амплитудно-частотные характеристики этих цепей таким образом, что они будут пропускать только сигналы нужной нам частоты, а остальные подавлять.

Фильтры высоких частот построены по схеме дифференцирующего звена (Рис.2.16). Согласно закону Ома для комплексных величин значение тока, протекающего по цепи, будет равно:

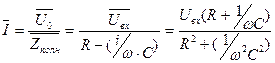2.16

Следовательно, напряжение на резисторе R равно:

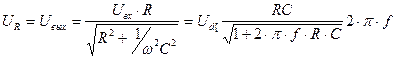2.17

где f = w/2p, а его фаза сдвинута относительно тока на угол j = arctg(-1/wRC).

На низких частотах полное сопротивление цепи определяется емкостным сопротивлением, которое в этом случае много выше сопротивления резистора. На высоких частотах наоборот сопротивление конденсатора становится пренеб­режимо малым по сравнению с активным сопротивлением.

Таким образом дифференцирующая цепь представляет собой делитель напряжения, выходное напряжение которого на высоких частотах приблизи­тельно равно входному, а низких частотах уменьшается до нуля, т.е. частотный фильтр, пропускающий высокие частоты и задерживающий низкие (рис.2.19).

С точки зрения амплитудно-частотных характеристик нетрудно объяснить и особенности прохождения импульсного сигнала через дифференцирующую цепь. Действительно, чем меньше длительность импульса T_и при заданной вели­чине постоянной времени цепи RC, тем выше частоты, соответствующие час­тотному спектру этого импульса и с тем меньшими искажениями они будут проходить через дифференцирующую цепь. Фронтам импульса соответствуют наиболее высокочастотные составляющие, которые всегда проходят через кон­денсатор с минимальными искажениями. Вершине прямоугольного импульса соответствуют наиболее низкочастотные составляющие, которые искажаются в наибольшей степени.

Фильтры низких частот формально являютсяэквивалентом интегри­рующей цепи. В схеме на рис. 2.18 сопротивление резистора R и емкостное со­противление конденсатора С образуют делитель напряжения, коэффициент де­ления которого зависит от частоты – n = U _k/ Uc = w· R·C

На малых частотах, таких, что wRC = n =>> 1, активное сопротив­ление существенно превышает емко­стное, R>>1/wC, и напряжение на выходе фильтра практически равно входному. На высоких частотах на­оборот, емкостное сопротивление конденсатора близко к нулю и ко­эффициент передачи цепи стремится к нулю (рис.2.20).

Фильтры нижних частот и со­ответствующие им интегрирующие цепи имеют большое значение в из­мерительной технике. Прежде всего, с их по­мо­щью можно устранить влияние на измерительный сигнал.высокочастотных помех и сущест­венно уменьшить уровень шумов. Требуется также иметь в виду, что любая ли­ния связи (провода и кабели) имеют собственную паразитную емкость, которая включена параллельно сопротивлению нагрузки и образует вместе с этим сопро­тивлением интегрирующую цепь, которая может существенно искажать измери­тельный сигнал. Например, линия, состоящая из двух проводов, расположенных на некотором расстоянии друг от друга, имеет собственную емкость С равную:

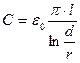
где e₀ = 8,85 пф/м – диэлектрическая постоянная вакуума, l – длина проводни­ков, r – радиус проводов, d – расстояние между ними. Отсюда следует, что при r =0,1 мм и d =1мм емкость 1 погонного метра линии будет равна примерно 10 пФ/м.

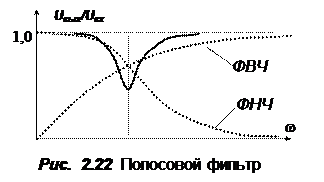При соответствующем выборе значений сопротивления и емкости комби­нация из фильтра верхних и фильтра нижних частот позволяет получить по­лосовой фильтр (Рис. 2.22), который пропускает (или наоборот обрезает) сигналы в не­котором диапазоне частот. Еще больше возможностей по частотной фильтра­ции предоставляют многозвен-ные фильтры высоких порядков, кото-рые позволяют получать АЧХ та­ких фильтров близкие к прямоугольным.

RLC цепи.

С точки зрения физических процессов индуктивность является зеркаль­ным аналогом емкости. В цепях с индуктивностью точно также могут существо­вать интегрирующие и дифференцирующие звенья. Но по нескольким причи­нам. в электроизмерительных системах индуктивности играют меньшую роль, чем емкости.

Во-первых, с чисто практической точки зрения индуктивности оказыва­ются существенно дороже конденсаторов и имеют значительно больший размер. Во-вторых, собственная индуктивность элементов конструкции электронных устройств как правило на порядки величины меньше их емкости и, соответст­венно, реактивное сопротивление линий переменного тока и их амплитудно-частотные характеристики определяются в первую очередь наличием емкостей, а не индуктивностей. В-третьих, катушки индуктивности имеют собственное ак­тивное сопротивление, наличие которого приводит к потерям энергии в элек­трической цепи.

Использование индуктивностей в измерительной технике в основном свя­зано с явлением резонанса. Если в цепи переменного тока присутствуют емкость и индуктивность, то при частоте, называемой резонансной частотой

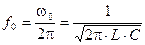2.17

возникает явление электрического резонанса. В зависимости от схемы соедине­ния емкости и индуктивности различают два случая.

· Резонанс токов, параллельный резонанс (рис. 2.23) - на резонансной частоте в LC цепи в отсутствии омического сопротивления в в ее элементах протекает бес­конечно большой ток, но полный импеданс этой цепи равен бесконечности - в узком интервале частот цепь не оказывает влияния на коэффициент передачи.

· Резонанс напряжений, последовательный резонанс (рис.) - при резонанс­ной частоте импеданс LC цепи падает до нуля, коэффициент передачи также становится равным 0, но при отсутствии активного сопротивления на

каждом из элементов напряжение может нарастать до бесконечности.

Резонансные схемы используются в измерительной технике в нескольких ос­новных случаях.

Пусть чувствительный элемент датчика представляет собой емкость или ин­дуктивность, значения которых изменяются под воздействием некоторого физи­ческого фактора. Если эти индуктивность или емкость включить в измеритель­ный резонансный контур, то можно очень точно определить изменение резо­нансной частоты этого контура и зная ее вычислить изменение индуктивности L или емкости C и далее измеряемую физическую величину

Пусть имеется очень слабый узкополосный периодический сигнал на фоне интенсивных шумов и помех. Тогда можно применить резонансный частотный LC фильтр, который будет пропускать сигнал только в очень узком диапазоне частот, совпадающем с частотой полезного сигнала.

От источников питания измерительной аппаратуры часто требуется практи­ческое полное отсутствие пульсаций выходного напряжения на частоте электри­ческой сети (50 Гц и более высокие гармоники). Резонансные LC фильтры обес­печат и лучшую фильтрацию напряжения, чем RC фильтры и, что очень сущест­венно, будут иметь серьезное преимущество, связанное с отсутствием омиче­ских потерь.

Дата добавления: 2015-03-31