Мосты переменного тока

При использовании мостовых схем на переменном токе условие равнове­сия имеет тот же вид, но для комплексных сопротивлений, входящих в ее со­став:

Z₁×Z₄ = Z₂×Z₃ (2.27)

где Z - комплексные величины, равные сумме активного и реактивного сопротивлений Z= R+jX. Следовательно, уравнение (2.27) должно быть пре­образовано в систему из двух уравнений для действительной и мнимой части:

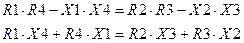
Эти два условия должны выполняться одновременно. Следовательно, если в мостах постоянного тока условие обеспечения равновесия моста может достигаться регулировкой только одного сопротивления, то мостах перемен­ного тока для уравновешивания моста необходима одновременная регули­ровка не менее 2-х параметров.

Еще одна трудность заключается в том, что при получении условия (2.27) мы не учитывали возможность появления фазо­вых сдвигов между сигналами в различных плечах моста. По этим причинам мосты переменного тока обычно регулируются только вручную методом по­следовательных приближений.

Существует несколько частных случаев, когда состояние равновесия мо­жет быть достигнуто регулировкой только одного параметра.

1.Сопротивления в плечах моста имеют чиcто реактивный характер, R1=R2=R3=R4=0, Условием равновесия в этом случае будет Х1·Х4=Х2·Х3.

2. Реактивное сопротивление элементов в плечах моста отсутствует. Тогда условие равновесия не будет отличаться от условия для моста постоянного тока (2ХХ).

3. Соседние плечи моста имеют одинаковый характер сопротивления – два чисто активный, а два – чисто реактивный:

R1, R2=0, X3, X4=0, R3, R4 ¹0, X1, X2¹0

2.8.4. Дифференциальные схемы электрических изме­рений.

Ø Дифференциальные (или разностные) схемы реализуют диффе­ренциальный метод сравнения и реагируют на разность токов или напряжений в двух связанных электрических конту­рах.

Дифференциальные измерительные схемы используются для измерений малых изменений сопротивления или ЭДС в случаях, когда:

Ø Требуется измерение малого полезного сигнала датчика на фоне боль­шого постоянного или переменного напряжения

Ø Величина сигнала датчика определяется смещением его чувствитель­ного элемента от некого положения равновесия.

Ø Существует необходимость снижения уровня шумов и помех, наведен­ных в датчике и соединительных проводах.

Ø Требуется минимизации влияния нестабильности питающего напряже­ния на результат измерения

В простейшей дифференциальной схеме (рис. 2.54) в измерительную цепь включены датчик – источник ЭДС U1, и источник опорного напря­жения U2. Измерительный прибор с внутренним сопротивлением R _g реги­стрирует ток I_d, равный разности то­ков в каждой из ветвей схемы:

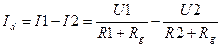2.28

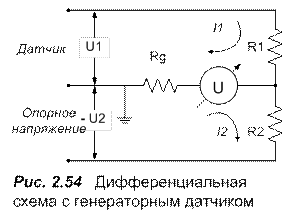Здесь надо отметить два момента. Во-первых, при выводе формулы (2.28) неявно предполагается, что значения сопротивлений R1 и R2 много больше внутреннего сопротивления датчика и источника опорного напряжения. Во-вторых, схема на рис. 2.54 по своей сути полностью аналогична схеме диф­ференциального операционного усилителя, рассмотренной ранее в первой части (рис. 1.16)

Возможны два принципиально разных варианта применения рассматриваемой дифференциальной схемы.

1. Пусть сигнал с датчика представляет собой медленно меняющуюся величину на фоне значительного постоянного сигнала, причем информатив­ную нагрузку несет именно изменяющаяся составляющая, U1=U0+DU. Если при этом установить величину опорного напряжения равной сигналу датчика в исходном состоянии, U2 = U0, а значения сопротивлений R1 и R2 подобрать равными друг другу, R1=R2, то в исходном состоянии суммарный ток через сопротивление R _g будет равен нулю, I_d =0. При изменении ЭДС датчика через измерительный прибор начнет протекать ток D I_d, величина которого будет равна:

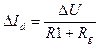
Т.е. измерительный прибор будет фиксировать только переменную (изме­няющуюся) составляющую сигнала.

2. Пусть сигнал с датчика представляет собой постоянный или перио­дический полезный (информативный) сигнал на который через подводящие провода накладывается значительная помеха или шум - U1=U0+U_ш,Тогда если на второй вход дифференциальной схемы подать не опорное напряже­ние, а только напряжение шума (помехи) U_ш, то на выходе дифференциаль­ной схемы мы будем иметь сигнал, очищенный от помех. Т.е, величина тока в измерительной цепи будет определяться только полезным сигналом:

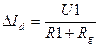
В принципе отделить постоянный сигнал от переменного, выделить низкочастотный полезный сигнал на фоне высокочастотный шумов и помех можно с использованием различных частотных фильтров. Принципиальное отличие дифференциальной схемы состоит в том, что ее амплитудно-частот­ная характеристика в первом приближении может считаться абсолютно пло­ской. Следовательно, в процессе измерения дифференциальная схема не вно­сит амплитудных и частотных искажений в сигнал датчика.

Дифференциальные схемы часто используются и с пассивными (пара­метрическими) датчиками. В схеме подключения такого датчика (рис. 2.55), которая внешне напоминает структуру мостовой схемы, сопротивления R1 и R2 называются выравнивающими сопротивлениями, задача которых состоит в том, чтобы обеспечить постоянство электрического потенциала в точке подключения измерительного прибора к источнику ЭДС.

При R1 = R2 ~ Rпр << Rд, Ro токчерез измерительный прибор равен:

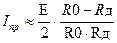
Следовательно, относительное изменение тока, которое может вызываться как изменениями сопротивления датчика (полезный сигнал), так флуктуа­циями (дрейфом) напряжения питания E, наведенными помехами и т.п., бу­дет равно:

Если выбрать величину сопротивления R0 примерно равной величине со­противления датчика, R0» Rд, то основной вклад в изменение тока будет вносить именно полезный сигнал, связанный с изменением сопротивления датчика, а не вариации, например, напряжения электропитания. Отметим, что если величина выравнивающих сопротивлений будет близка к собственному сопротивлению датчика, то чувствительность и линейность мостовой схемы резко уменьшатся.

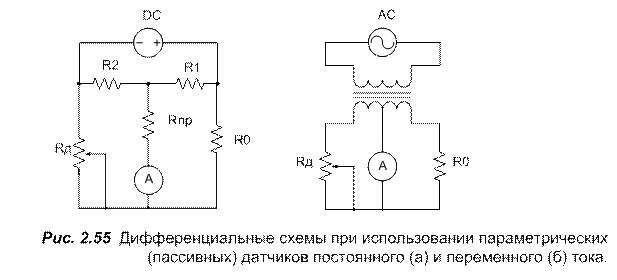
Если активные сопротивления заменить в дифференциальной схеме заме­нить на реактивные (емкостные, индуктивные) или комплексные, R Þ Z, то все приведенные выше рассуждения будут справедливы и для цепей пере­менного тока. Следовательно, дифференциальные схемы можно использо­вать при измерении как постоянных, так переменных сигналов в схемах с ак­тивными и пассивными датчиками.

Например, датчик представляет собой источник напряжения вместе с вы­равнивающими сопротивлениями R1, R2, а сопротивление в ветвях диффе­ренциальной цепи строго равны между собой (сопротивления R0 = Rд на ри­сунке). Тогда величина тока в измерительной цепи будет зависеть только от изменения соотношения между величинами сопротивлений R1 и R2, т.е. от изменения внутреннего сопротивления (импеданса) датчика.

Дата добавления: 2015-03-31