Примеры решения задач 1 страница

B H

ЭЛЕКТРОМАГНЕТИЗМ

· Закон Био — Савара — Лапласа

dB [ dl,r ] ,

где dB — магнитная индукция поля, создаваемого элементом i проводника с током; m — магнитная проницаемость; m₀ — магнитная постоянная (m₀ =4 p · 10 ^-7 Гн/м); dl — вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I — сила тока; r — радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора dB выражается формулой

dB 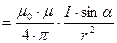dl,

где a — угол между векторами dl и r.

· Магнитная индукция В связана с напряженностью Н магнитного поля (в случае однородной, изотропной среды) соотношением

или в вакууме

B ₀= μ ₀ ∙ H.

· Магнитная индукция в центре кругового проводника с током

В ,

где R — радиус кривизны проводника.

· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

В ,

где r — расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводником

В .

Обозначения ясны из рис.1, а. Вектор индукции В перпенди­кулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.

При симметричном расположении концов проводника относи­тельно точки, в которой определяется магнитная индукция (рис. 1, б), 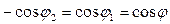и, следовательно,

В

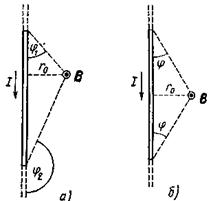
Рис. 1

· Магнитная индукция поля, создаваемого соленоидом в сред­ней его части (или тороида на его оси),

В

где п — число витков, приходящих­ся на единицу длины соленоида;

I — сила тока в одном витке.

· Принцип суперпозиции маг­нитных полей: магнитная индук­ция В результирующего поля равна векторной сумме магнитных индукций В₁, В₂ ,..., В _n складываемых полей, т. е.

B В_i.

В частном случае наложения двух полей

В = В₁ + В₂,

а модуль магнитной продукции

,

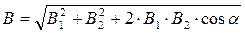
где a — угол между векторами В₁ и В₂.

• Закон Ампера. Сила, действующая на проводник с током в магнитном поле,

F =[ l,B ]∙ I,

где I — сила тока; l — вектор, равный по модулю длине l проводника и совпадающий по направлению с током; В — магнитная индукция поля.

Модуль вектора F определяется выражением

F = B∙I∙l∙sin α,

где α — угол между векторами l и В.

• Сила взаимодействия двух прямых бесконечно длинных па­раллельных проводников с токами I ₁ и I ₂, находящихся на расстоянии d друг от друга, рассчитанная на отрезок проводника длиной l выражается формулой

.

• Магнитный момент контура с током

p_m = I ∙ S,

где S — вектор, равный по модулю площади S, охватываемой кон­туром, и совпадающий по направлению с нормалью к его плоскости.

• Механический момент, действующий на контур с током, по­мещенный в однородное магнитное поле,

M= [ p_m ∙ B ].

Модуль механического момента

M=p_m∙B∙sinα,

где α — угол между векторами р_m и В.

• Потенциальная (механическая) энергия контура с током в магнитном поле

П_мех= p_m∙B =p_m∙B∙cosα.

• Сила, действующая на контур с током в магнитном поле (из­меняющемся вдоль оси x),

,

где —изменение магнитной индукции вдоль оси Ох, рассчи­танное на единицу длины; α — угол между векторами р_m и В.

• Сила F, действующая на заряд Q, движущийся со скоростью υ в магнитном поле с индукцией В (сила Лоренца), выражается фор­мулой

F = Q [ υ, B ] или F=|Q|uB sina,

где a — угол, образованный вектором скорости υ движущейся ча­стицы и вектором В индукции магнитного поля.

· Циркуляция вектора магнитной индукции В вдоль замкну­того контура

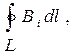
где B_i — проекция вектора магнитной индукции на направление элементарного перемещения dl вдоль контура L. Циркуляция век­тора напряженности Н вдоль замкнутого контура

,

· Закон полного тока (для магнитного поля в вакууме)

где m₀ =4∙π∙10^-7 Гн/м - магнитная постоянная; 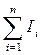- алгебраическая сумма токов, охватываемых контуром; п - число токов.

Закон полного тока (для произвольной среды)

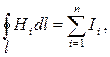
· Магнитный поток Ф через плоский контур площадью S:

а) в случае однородного поля

Ф = BS cos a; или Ф = B _n S,

где a — угол между вектором нормали n к плоскости контура и век­тором магнитной индукции В; В _n — проекция вектора В на нормаль n (B _n =B cos a);

б) в случае неоднородного поля

где интегрирование ведется во всей поверхности S.

· Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида,

где Ф — магнитный поток через один виток; N — число витков со­леноида или тороида.

· Магнитное поле тороида, сердечник которого составлен из двух частей, изготовлен­ных из веществ с раз­личными магнитными проницаемостями:

а) магнитная индук­ция на осевой линии тороида

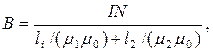
где I — сила тока в об­мотке тороида; N — чис­ло ее витков; l ₁ и l₂ -­ длины первой и второй частей сердечника торо­ида; m₁ и m₂ —магнитные проницаемости ве­ществ первой и второй частей сердечника торо­ида; m₀ —магнитная постоянная

б) напряженность магнитного поля на осе­вой линии тороида в первой и второй частях сердечника

H ₁= B /(m₁ ∙m₂); H ₁= B /(m₂ ∙m₀ );

в) магнитный поток в сердечнике тороида

или по аналогии с законом Ома (формула Гопкинсона)

Ф_m=F_m/R_m,

где F_m - магнитодвижущая сила; R_m - полное магнитное сопро­тивление цепи;

г) магнитное сопротивление участка цепи

R_m=l/ (μ∙μ₀S).

• Магнитная проницаемость μ, ферромагнетика связана с маг­нитной индукцией В поля в нем и напряженностью Н намагничи­вающего поля соотношением

μ = B/ (μ₀H).

• Работа по перемещению замкнутого контура с током в маг­нитном поле

A = I D Ф,

где D Ф — изменение магнитного потока, пронизывающего поверх­ность, ограниченную контуром; I — сила тока в контуре.

• Основной закон электромагнитной индукции (закон Фарадея — Максвелла)

,

где 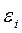— электродвижущая сила индукции; N — число витков кон­тура; Y — потокосцепление.

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной I, движущегося со скоростью u в однородном магнитном поле,

U=B∙l∙u∙sina,

где a — угол между направлениями векторов скорости u и магнит­ной индукции В;

б) электродвижущая сила индукции 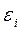, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью со в однородном магнитном поле с индукцией В

,

где wt — мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.

• Количество электричества Q, протекающего в контуре,

,

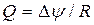где R — сопротивление контура; D Y — изменение потокосцепления.

•Электродвижущая сила самоиндукции возникающая в замкнутом контуре при изменении силы тока в нем,

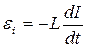, или ,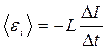

где L — индуктивность контура.

• Потокосцепление контура Y = LI, где L — индуктивность контура.

• Индуктивность соленоида (тороида)

.

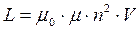Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнит­ной проницаемости следует пользоваться графиком зависимости В от Н (см. рис. 24.1), а затем формулой

.

• Мгновенное значение силы тока I в цепи, обладающей актив­ным сопротивлением R и индуктивностью L:

а) после замыкания цепи

,

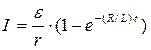где ε - ЭДС источника тока; t— время, прошедшее после замы­кания цепи;

б) после размыкания цепи

,

где l ₀ - сила тока в цепи при t=0, t - время, прошедшее с момен­та размыкания цепи.

• Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, определяется формулой

,

где I — сила тока в контуре.

• Объемная (пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида)

.

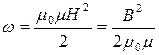• Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

,

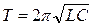где L — индуктивность контура; С — его электроемкость.

• Связь длины электромагнитной волны с периодом Т и час­тотой υ колебаний

или ,

где с — скорость электромагнитных волн в вакууме (с=3∙10⁸ м/с).

• Скорость электромагнитных волн в среде

где ε - диэлектрическая проницаемость; μ - магнитная проницае­мость среды.

Пример 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I =60 А, расположены на расстоянии d =10 см друг от друга. Определить магнитную индукцию В в точке, отстоящей от одного про­водника на расстоянии r₁ =5 см и от другого — на расстоянии r₂ =12 см.

Решение. Для нахождения магнитной индукции в указанной точ­ке А (рис. 2) определим

Рис. 2 направле­ния векторов индукций В ₁ и В ₂ по лей, создаваемых каждым проводни­ком в отдельности, и сложим их геометрически, т. е. B = B ₁+ B ₂. Модуль индукции найдем по теоре­ме косинусов:

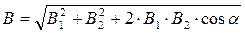
Значения индукций Bi и В₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂ от провода до точки, индукцию в которой мы вычисляем:

,

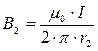
Подставляя B₁ и В₂ в формулу (1) и вынося за знак корня, получим

. (2)

Убедимся в том, что правая часть этого равенства дает единицу магнитной индукции (Тл):

Здесь мы воспользовались определяющей формулой для маг­нитной индукции (В=М_mак /р_п). Откуда следует, что

.

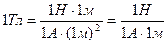Вычисляем cosa. Заметим, что a= /_ DAC. Поэтому по теореме косинусов запишем

,

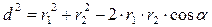где d — расстояние между проводами. Отсюда

.

Подставив данные, вычислим значение косинуса: cos a = 0,576.

Подставив в формулу (2) значения m₀, I, r₁, r₂ и cos b, найдем В =286 мкТл.

Пример 2. По двум длинным прямолинейным проводам, находя­щимся на расстоянии r=5 см друг от друга в воздухе, текут токи I =10 А каждый. Определить магнитную индукцию В поля, создаваемого то­ками в точке, лежащей по­середине между проводами, для случаев: 1) провода параллельны, токи текут в одном направлении (рис. 3, а); 2) провода параллельны­,токи текут в про­тивоположных направле­ниях (рис. 3, б); 3) про­вода перпендикулярны, на­правление токов указано на рис. 3, в.

Рис. 3

Решение: Результирующаяиндукция магнитного поля равна векторной сумме: B=B₁+B₂, где B₁ — индукция поля, создаваемого током 1 ₁; В₂ — индукция поля создаваемого током I ₂.

Если B₁ и В₂ направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:

В=В₁+В₂. (1)

При этом слагаемые В₁ и В₂ должны быть взяты с соответствую­щими знаками. В данной задаче во всех трех случаях модули индукций В₁ и В₂ одинаковы, так как точки выбраны на равных расстояниях от про­водов, по которым текут равные токи. Вычислим эти индукции по формуле

B=m₀I/(2pr). (2)

Подставив значения величин в формулу (2), найдем модули В₁ и В₂:

В₁=В₂=80 мкТл.

1-й случай. Векторы B₁ и В₂ направлены по одной прямой (рис.3, а); следовательно, результирующая индукция В опреде­ляется по формуле (1). Приняв направление вверх положительным, вниз — отрицательным, запишем: В ₁ = - 80 мкТл, В ₂=80 мкТл.

Подставив в формулу (1) эти значения В ₁и B ₂, получим

В=В ₁ +В₂=0.

2-й случай. Векторы В ₁ и В ₂ направлены по одной прямой в одну сторону (рис. 3, б). Поэтому можем за­писать

В ₁ =В ₂ = – 80 мкТл.

Подставив в формулу (1) значения B ₁ и В ₂ получим

В=В ₁ +В ₂ = – 160 мкТл.

3-й случай. Векторы индукций магнит­ных полей, создаваемых токами в точке, лежащей посередине между проводами, взаимно перпендикулярны (рис. 3, в). Результирующая индукция по модулю и направлению является диагональю квадра­та, построенного на векторах В ₁ и В ₂. По теореме Пифагора найдем

(3)

Подставив в формулу (3) значения В ₁и В ₂, получим B =113 мкТл.

Пример 3. Определить магнитную индукцию В поля, создаваемо­го отрезком бесконечно длинного прямого провода, в точке, равно­удаленной от концов отрезка и находящейся на расстоянии r ₀ = 20 см от середины его (рис. 4). Сила тока I, текущего по про­воду, равна 30 А, длина l отрезка равна 60 см.

Решение. Для определения магнитной индукции поля, соз­даваемого отрезком провода, воспользуемся законом Био -Савара-Лапласа: dB 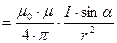dl (1)

Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу a. Выразим длину элемента dl проводника через da. Согласно рис. 4, запишем

. Рис. 4

Подставим это выражение dl в формулу (1):

dB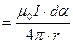

Но r — величина переменная, зависящая от a и равная 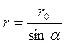. Подставив r в предыдущую формулу, найдем

(2)

Чтобы определить магнитную индукцию поля, создаваемого от­резком проводника, проинтегрируем выражение (2) в пределах от a₁ до a₂:

(3)

Заметим, что при симметричном расположении точки A относитель­но отрезка провода cos a₂= – cos a₁. С учетом этого формула (3) примет вид

.

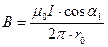Из рис. 4 следует

Подставив выражение cos a₁ в формулу (4), получим

∙ .

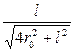Подставим числовые значения в формулу (5) и произведем вы­числения:

Пример 4. Длинный провод с током I =50 А изогнут под углом a=2p/3. Определить магнитную индукцию В в точке А (рис. 5). Расстояние d=5 см.

Решение. Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О. В соответ­ствии с принципом суперпозиции магнитных полей магнитная ин­дукция В в точке А будет равна геометрической сумме магнитных индукций B₁ и В₂ полей, создаваемых отрезками длинных проводов

1 и 2, т. е. В = В ₁ +В ₂. Магнитная индукция В ₂равна нулю. Это следует из закона Био — Савара — Лапласа, согласно которому в точках, лежащих на оси проводника, d В = 0([ dl,r ]=0).

Магнитную индукцию В ₁ найдем, воспользовавшись формулой (3), полученной в примере 3:

,

где r₀ — кратчайшее расстояние от проводника 1 до точки А (рис. 6)

В нашем случае α₁→0 (проводник длинный), α₂=α==2π/3 (cos α₂= cos (2π/3))=–½. Расстояние r ₀ =d sin (π−α)= d sin(π/3)= 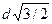. Тогда магнитная индукция

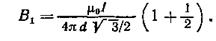
Так как В=В₁ (В₂= 0), то

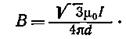
Вектор В сонаправлен с вектором В ₁ и определяется правилом правого винта. На рис. 6 это направление отмечено значком X (перпендикулярно плоскости чертежа от нас).

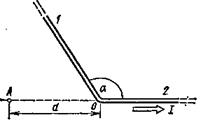
Рис. 5 Рис. 6

Проверка единиц аналогична проверке выполненной в примере 1.

Произведем вычисления:

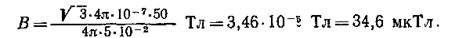
Пример 5. По тонкому проводящему кольцу радиусом R = 10 см течет ток I =80 А. Найти магнитную индукцию В в точке A, равно­удаленной от всех точек кольца на расстояние г=20 см.

Решение. Для решения задачи воспользуемся законом Био — Савара — Лапласа:

dB [ dl,r ] ,

где dB —магнитная индукция поля, создаваемого элементом тока Idl в точке, определяемой радиус-вектором r.

Рис. 7

Выделим на кольце элемент dl и от него в точку А проведем радиус-вектор г (рис. 7). Вектор d B направим в соответствии с правилом буравчика.

Согласно принципу суперпозиции магнитных полей, магнитная индукции В в точке А определяется интегралом

где интегрирование ведется по всем элементам dI кольца Разложим вектор d B на две составляющие: dB_┴ – перпендикулярную плоскости кольца и d B _║ — параллельную плоскости кольца, т. е.

d B= d B_^+ d B _½½. Тогда

Заметив, что из соображений симметрии и что векторы d B_┴ от различных элементов d I сонаправлены, заменим векторное суммирование, заменим векторное суммирование (интегрирование) скалярным:

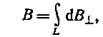
где (поскольку d I перпендикулярен r и, следовательно, sina=1). Таким образом,

После сокращения на 2π и замены cos β на R/r (рис. 7)

Выразим все величины в единицах СИ, произведем вычисления:

или

Вектор В направлен на осикольца (пунктирная стрелка на рис. 7) в соответствии с правилом буравчика.

Пример 6. бесконечно длинный проводник изогнут так, как это изображено на рис. 8. Радиус дуги окружности R =10 см. Определить магнитную индукцию В поля, создаваемого в токе О током I =80 A, текущим по этому проводнику.

Дата добавления: 2015-03-31