Примеры решения задач 2 страница. Решение. Магнитную индукцию В в точке О найдем, используя принцип суперпозиции магнитных полей В=∑Вi

Решение. Магнитную индукцию В в точке О найдем, используя принцип суперпозиции магнитных полей В=∑В_i. В на­шем случае проводник можно разбить на три части (рис. 9) два прямолинейных проводника (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда

B = B ₁+ B ₂+ B ₃

где B ₁, В ₂ и В ₃ — магнитные индукции поля в точке О, создавае­мые током, текущим соответственно на первом, втором и третьем участках проводника.

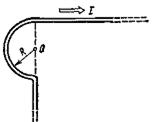
Рис. 8 Рис. 9

Так как точка О лежит на оси проводника 1, то В ₁=0и тогда

B=B₂+B₃

Учитывая, что векторы В ₂ и В ₃ направлены в соответствии с пра­вилом буравчика перпендикулярно плоскости чертежа от нас, гео­метрическое суммирование можно заменить алгебраическим:

В=В₂+В₃.

Магнитную индукцию поля В ₂можно найти, используя выраже­ние для магнитной индукции в центре кругового проводника с то­ком I:

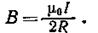
Так как магнитная индукция В ₂создается в точке О половиной такого кругового проводника с током, то, учитывая равный вклад в магнитную индукцию от каждой половинки проводника, можно написать

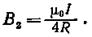
Магнитную индукцию В ₃найдем, используя формулу (3) при­мера 3:

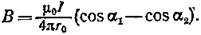
В нашем случае

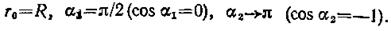
Тогда

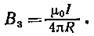
Используя найденные выражения для В₂ и В₃ получим

или

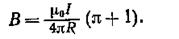
Произведем вычисления:

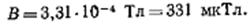
Пример 7. По двум параллельным прямым проводам длиной l =2,5 м каждый, находящимся на расстоянии d =20 см друг от дру­га, текут одинаковые токи I =1 кА. Вычислить силу F взаимодей­ствия токов.

Решение. Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток соз­дает магнитное поле, которое действует на другой проводник. Пред­положим, что оба тока (обозначим их 1_г и I ₂) текут в одном направ­лении.

Вычислим силу F ₁,₂, с которой магнитное поле, созданное током I ₁, действует на проводник с током I ₂. Для этого проведем магнит­ную силовую линию так (штриховая линия на рис. 10), чтобы она касалась проводника с током I ₂. По касательной к силовой линии проведем вектор магнитной индукции В ₁. Модуль магнитной индук­ции B ₁ определяется соотношением

(1)

Согласно закону Ампера, на каждый элемент второго проводника с током I ₂ длиной dl₂ действует в магнитном поле сила

Так как отрезок dl перпендикулярен вектору B ₁, то

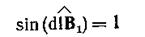
и тогда

(2)

Подставив в выражение (2) В ₁из (1), получим

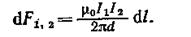
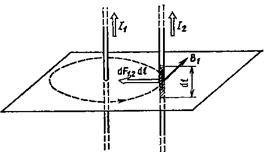
Рис. 10

Силу F _1,2 взаимодействия проводников с током найдем интегрированием по всей длине второго проводника;

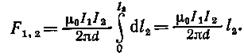
Заметив, что I ₁= I ₂= I и l₂=l, получим

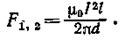
Убедимся в том, что правая часть этого равенства дает единицу силы

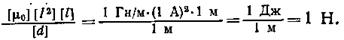
Произведем вычисления:

Сила F ₁,₂ сонаправлена с силой d F ₁,₂ (рис. 10) и определяется (в данном случае это проще) правилом левой руки.

Пример 8. Провод в виде тонкого полукольца радиусом R= 10 см находится в однородном магнитном поле (B =50 мТл). По проводу течет ток I =10 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводя­щие провода находятся вне поля.

Решение. Распо­ложим провод в плоско­сти чертежа перпенди­кулярно линиям маг­нитной индукции (рис. 11) и выделим на нем малый элемент d l с то­ком.

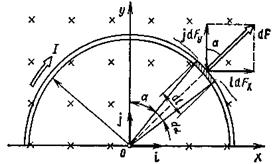
Рис. 11

На этот элемент тока Idl будет действо­вать по закону Ампера сила d F = I [dlB]. Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.

Используя симметрию, выберем координатные оси так, как это изображено на рис. 11. Силу d F представим в виде

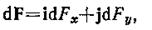
где i и j — единичные векторы (орты); dF_x и dF_y — проекции векто­ра d F на координатные оси Ох и Оу.

Силу F, действующую на весь провод, найдем интегрированием:

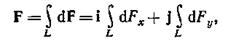
где символ L указывает на то, что интегрирование ведется по всей длине провода L.

Из соображений симметрии первый интеграл равен нулю

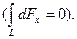тогда

(1)

Из рис. 11 следует, что

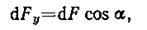
где dF— модуль вектора 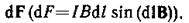Так как векторdlперпендикулярен вектору 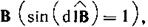то 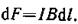Вы­разив длину дуги d l через радиус R иугол α, получим

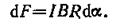
Тогда

Введем dF_y под интеграл соотношения (1) и проинтегрируем в пре­делах от -π/2 до +π/2 (как это следует из рис. 11):

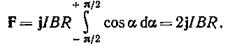
Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу (единичным вектором j).

Найдем модуль силы F:

Убедимся в том, что правая часть этого равенства дает единицу силы (Н):

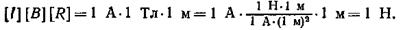
Произведем вычисления:

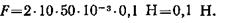
Пример 9. На проволочный виток радиусом г=10см, помещен­ный между полюсами магнита, действует максимальный механиче­ский момент М_max=6,5 мкН. Сила тока I в витке равна 2А. Опреде­лить магнитную индукцию В поля между полюсами магнита. Дей­ствием магнитного поля Земли пренебречь.

Решение. Индукцию В магнитного поля можно определить из выражения механического момента, действующего на виток с то­ком в магнитном поле,

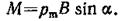(1)

Если учесть, что максимальное значение механический момент принимает при α=π/2(sin α=l), а также что p_m=IS, то формула (1) примет вид

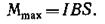
Отсюда, учитывая, что S= πr ², находим

(2)

Произведя вычисления по формуле (2), найдем

В =104 мкТл.

Пример 10. Квадратная рамка со стороной длиной а =2см, содер­жащая N=100 витков тонкого провода, подвешена на упругой нити, постоянная кручения С которой равна 10 мкН·м/град. Плоскость рамки совпадает с направлением линии индукции внешнего магнит­ного поля. Определить индукцию внешнего магнитного поля, если при пропускании по рамке тока I= 1А она повернулась на угол α=60°.

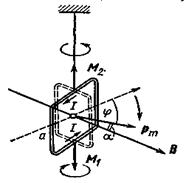Решение. Индукция В внешнего поля может быть найдена из условия равновесия рамки в поле. Рамка будет находиться в рав­новесии, если сумма механических моментов, действующих на нее, будет равна нулю:

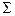M=0.

В данном случае на рамку действуют два момента (рис. 12): M ₁ — момент сил, с которым внешнее магнитное поле действует на рамку с током, и М ₂ — момент упругих сил, возникающих при за­кручивании нити, на которой рамка подвешена.

Рис. 12

Следовательно, формула (1) может быть переписана в виде

M ₁ + M ₂=0

Выразив М ₁и М ₂в этом равенстве через величины, от которых зависят мо­менты сил, получим

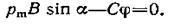(2)

Знак минус перед моментом М ₂ста­вится потому, что этот момент противо­положен по направлению моменту M ₁.

Если учесть, что p_m=ISN=Ia²N, где I — сила тока в рамке; S=a² — площадь рамки; N — число ее витков, равенство (2) перепишем в виде

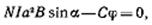откуда

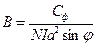(3)

Из рис. 12 видно, что α=π/2 — φ, значит, sin α=cos φ. С учетом этого равенство (3) примет вид

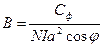(4)

Значение постоянной кручения С, рассчитанной на градус (а не радиан, как это следовало бы выразить в СИ), запишем в виде

так как значение угла φ также дано в градусах.

Подставим данные в формулу (4) и произведем вычисления:

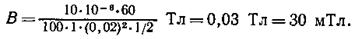
Пример 11. Плоский квадратный контур со стороной длиной а = 10 см, по которому течет ток I = 100 А, свободно установился в од­нородном магнитном поле индукцией В= 1Тл. Определить работу A, совершаемую внешними силами при повороте контура относи­тельно оси, проходящей через середину его противоположных сто­рон, на угол: 1) φ₁=90°; 2) φ₂= З⁰. При повороте контура сила тока в нем поддерживается неизменной.

Решение. На контур с током в магнитном поле действует механический момент

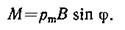(1)

По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю

(М =0), а значит φ=0, т. е. векторы р_m и В совпадают по направле­нию.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремить­ся возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла φ поворота), то для подсчета работы применим формулу работы в дифференциальной форме

dA = Mdj (2)

Подставив сюда выражение М по формуле (1) и учтя, что р_т= IS=Ia², где I — сила тока в контуре, S=a² — площадь контура, получим

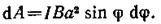
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

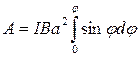(3)

1. Работа при повороте на угол φ₁=90⁰

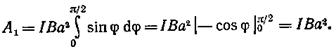(4)

Убедимся в том, что правая часть этого равенства дает единицу работы (Дж):

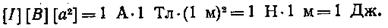
После вычисления по формуле (4) найдем A₁=l Дж.

2. Работа при повороте на угол ф₂=3°. В этом случае, учитывая, что угол ф₂ мал, заменим в выражении (3) sin φ на φ:

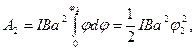(5)

Выразим угол φ₂ в радианах (см. табл. 9)

Φ₂=3⁰=3·l,75·10^-2 рад=0,0525 рад.

После подстановки значений I, В, а и φ₂ в формулу (5) получим А ₂=1,37 мДж.

Пример 12. Электрон, пройдя ускоряющую разность потенциа­лов U =400 В, попал в однородное магнитное поле с индукцией B =1,5 мТл. Определить: 1)радиус R кривизны траектории; 2)ча­стоту п вращения электрона вмагнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

Решение. 1. Радиус кривизны траектории электрона опре­делим, исходя из следующих соображений: на движущийся в маг­нитном поле электрон действует сила Лоренца F. (Действием силы тяжести можно пренебречь.) Вектор силы Лоренца перпендикуля­рен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение а_n : F=ma_n. Подставив сюда выражения F и а_n, получим

| e | uB sin a=mu²/R, (1)

где е, u, т — заряд, скорость, масса электрона; В — индукция маг­нитного поля; R — радиус кривизны траектории; a — угол между направлениями векторов скорости v и индукции В (в нашем случае v ^ B и a = 90°, sin a =l).

Из формулы (1) найдем

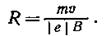(2)

Входящий в выражение (2) импульс mu выразим через кинетическую энергию Т электрона:

(3)

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством Т= | e | U. Подставив это выражение Т в формулу (3), получим

Тогда выражение (2) для радиуса кривизны приобретает вид

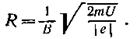
Убедимся в том, что правая часть этого равенства дает единицу длины (м):

м

После вычисления по формуле (4) найдем

R =45 мм.

2. Для определения частоты вращения воспользуемся формулой связывающей частоту со скоростью и радиусом кривизны траектории,

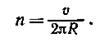
Подставив R из выражения (2) в эту формулу, получим

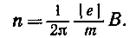
Произведя вычисления, найдем n =4,20 × 10⁷ c^-1 .

Пример 13. Электрон, имея скорость u =2 Мм/с, влетел воднородное магнитное поле с индукцией В =30 мТл под углом a=30° к направлению линий индукции. Определить радиус R и шаг h винтовой линии, покоторой будет двигаться электрон.

Решение. Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции В и скорости v частицы:

F=QuB sin a, (1)

где Q — заряд частицы.

В случае, если частицей является электрон, формулу (1) можно записать в виде

F= |e| uB sin a.

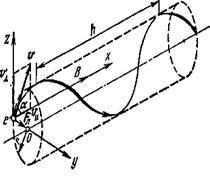
Так как вектор силы Лоренца перпендикулярен вектору скоро­сти, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная си­ла, перпендикулярная скоро­сти, вызывает Рис. 13

движение по окружности. Следовательно, электрон, влетевший в маг­нитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, рав­ной поперечной составляю­щей u ₁скорости (рис. 13); одновременно он будет дви­гаться и вдоль поля со ско­ростью u _||:

u _|| = u sin a, u _|| = u cos a.

В результате одновременного участия в движениях по окружно­сти и по прямой электрон будет двигаться по винтовой линии.

Радиус окружности, по которой движется электрон, найдем сле­дующим образом. Сила Лоренца F сообщает электрону нормальное ускорение а_п. По второму закону Ньютона, F=ma_n, где F= | e | u ₁ B и a_n=u ² ^ R,. Тогда

| e | u ^ B = mu₂²/R,

откуда после сокращения на u _zнаходим радиус винтовой линии:

Подставив значения величин т, u, e, В и a и произведя вычисле­ния, получим

R =0,19 мм.

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью u _x завремя, которое понадобится электрону для того, чтобы совершить один оборот,

h = u _|| T (2)

где T=2pR/u _^ — период вращения электрона. Подставив это выра­жение для Т в формулу (2), найдем

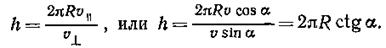
Подставив в эту формулу значения величин p, R и a и вычислив, получим h =2,06 мм.

Пример 14. Электрон движется воднородном магнитном поле с индукцией В=0,03 Тл поокружности радиусом r=10см. Опреде­лить скорость u электрона.

Решение. Движение электрона по окружности в однородном магнитном поле совершается под действием силы Лоренца (см. примеры 1 и 2). Поэтому можно написать

(1)

откуда найдем импульс электрона:

р=тu= | е | Вr. (2)

Релятивистский импульс выражается формулой

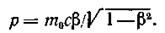
Выполнив преобразования, получим следующую формулу для определения скорости частицы:

(3)

В данном случае р= | e | Br. Следовательно,

В числитель и знаменатель формулы (4) входит выражение |е| В_r(т ₀ с). Вычислим его отдельно:

|е| В_r / (m ₀c) = 1,76.

Подставив найденное значение отношения |е| В_r(т ₀ с) в формулу (4), получим

b = 0,871, или u = с b= 2,61-10⁸ м/с.

Электрон, обладающий такой скоростью, является релятивистским.

Пример 15. Альфа-частица прошла ускоряющую разность потенциалов U =104 В и влетела в скрещенные под прямым углом электрическое (E =10 кВ/м) и магнитное (B =0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.

Решение. Для того чтобы найти отношение заряда Q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частиц:

QU = mu ²/2,

откуда

Q/m=u²/(2U). (1)

Скорость u альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:

а) сила Лоренца F _л=Q[ vВ ], направленная перпендикулярно скорости v и вектору магнитной индукции В;

б) кулоновская сила F_K =Q E, сонаправленная с вектором напряженности Е электростатического поля (Q >0).

Сделаем рисунок с изображением координатных осей и векторных

величин. Направим вектор магнитной индукции В вдоль оси О_z (рис. 14), скорость v—в положительном направлении оси Ох, тогда F _л и F _k будут направлены так, как это указано на ри­сунке.

Альфа-частица не будет испытывать отклонения, если геометри­ческая сумма сил F _л+ F_k будет равна нулю. В проекции на ось

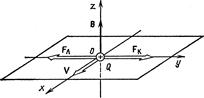
Рис. 14

Оу получим следующее равенство (при этом учтено, что вектор ско­рости v перпендикулярен вектору магнитной индукции В и sin (v ^Ù B)=l):

QE—QuB = O,

откуда

u =E/B.

Подставив это выражение скорости в формулу (1), получим

Q/m=E²(2UB²).

Убедимся в том, что правая часть равенства дает единицу отно­шения заряда к массе (Кл/кг):

Произведем вычисления: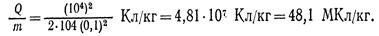

Пример 16. В одной плоскости с бесконечно длинным прямым проводом, по которому течет ток I =50 А, расположена прямоуголь­ная рамка так, что две большие стороны ее длиной l =65 см парал­лельны проводу, а расстояние от провода до ближайшей из этих сторон равно ее ширине. Каков магнитный поток Ф, пронизываю­щий рамку?

Решение. Магнитный поток Ф через поверхность площадью S определяется выражением

Рис. 15

В нашем случае вектор магнитной индукции В перпендикулярен плоскости рамки. Поэтому для всех точек рамки В_n=В. Магнитная индукция В, создаваемая бесконечно длинным прямым проводником с током, определяется формулой

,

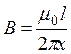где x— расстояние от провода до точки, в которой определяется В.

Для вычисления магнитного потока заметим, что так как В зависит от х и элементарный поток Ф будет также за­висеть от х, то

dФ=B(x)dS.

Разобьем площадь рамки на узкие элементарные площадки длиной l, шири­ной dx и площадью dS=ldx (рис. 15). В пределах этой площадки магнитную индукцию можно считать постоянной, так как все части площад­ки равноудалены (на расстояние х) от провода. С учетом сделанных замечаний элементарный магнитный поток можно записать в виде

dФ=

Проинтегрировав полученное выражение в пределах от x ₁ =a до х₂=2а, найдем

|_p^2p.

Подставив пределы, получим

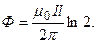
Убедимся в том, что правая часть полученного равенства дает единицу магнитного потока (Вб): [m₀] [ I ] [ l ]= Гн/м ×1 А ×1 м=1 Вб. Произведя вычисления по формуле (1), найдем Ф=4,5 мкВб.

Пример 17. Определить индукцию В и напряженность Н магнит­ного поля на оси тороида без сердечника, по обмотке которого, со­держащей N =200 витков, идет ток I =5 А. Внешний диаметр d ₁тороида равен 30 см, внутренний d ₂ = 20 см.

Решение. Для определения напряженности магнитного поля внутри тороида вычислим циркуляцию вектора Н вдоль линии маг­нитной индукции поля: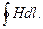

Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряженности одинаковы. Поэтому в выражении циркуля­ции напряженность Н можно вынести за знак интеграла, а интегри­рование проводить в пределах от нуля до 2 p r, где r — радиус ок­ружности, совпадающей с линией индукции, вдоль которой вычис­ляется циркуляция,

(1)

С другой стороны, в соответствии с законом полного тока цир­куляция вектора напряженности магнитного поля равна сумме то­ков, охватываемых контуром, вдоль которого вычисляется цирку­ляция:

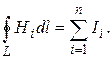(2)

Приравняв правые части равенств (1) и (2), получим

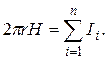(3)

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2prH=-NI, откуда

Дата добавления: 2015-03-31