Пример 13

ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ

ОЦЕНКА НАДЕЖНОСТИ ОПРЕДЕЛЕНИЯ СРЕДНЕАРИФМЕТИЧЕСКОГО С ИСПОЛЬЗОВАНИЕМ

Доверительным называется интервал , который с заданной надежностью покрывает оцениваемый параметр. Для оценки математического ожидания случайной величины X, распределенной по нормальному закону, при известной дисперсии 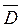служит доверительный интервал

, (3.29)

где – точность оценки;

n – объем выборки;

– математическоеожидание;

– доверительная вероятность;

– аргумент функции Лапласа;

и – границы доверительного интервала.

Построить доверительный интервал для математического ожидания случайной величины X при Имеем:

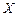
	50,91	50,23	49,51	48,79	48,10	47,38	46,60	47,47	50,95	54,35	57,33	57,57

В качестве исходного положения примем 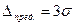, где 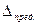- предельная величина погрешности измерения.

По табл. 3 (см. приложение) для и 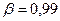находим 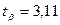, откуда

Доверительный интервал будет

.

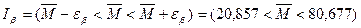Задача 29.

Произведено 16 измерений теодолитом 4Т30П горизонтального угла полным приемом, со СКП 0,5'. Найдите доверительный интервал погрешностей теодолита с надежностью =0,95. Предполагается, что погрешности измерений распределены нормальному закону.

Задача 30.

Случайная величина X имеет нормальное распределение с известным СКП 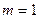. Найдите доверительные интервалы для оценки неизвестного математического ожидания по выборочным средним , если объем выборки n =25 и задана надежность оценки =0,9.

Задача 31.

Решить задачи 13, 14 и 15 с использованием доверительных интервалов.

Дата добавления: 2015-03-31