
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры. Задание 1: Найти частные производные следующих функций:
|
|
|
|
Задание 1: Найти частные производные следующих функций:
1) 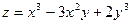 ;
;
2) 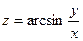 ;
;
3) 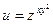 .
.
Решение: 1) При нахождении частной производной по 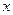 будем рассматривать
будем рассматривать 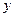 как величину постоянную. Тогда получим
как величину постоянную. Тогда получим
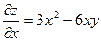 .
.
Аналогично, рассматривая 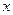 как величину постоянную, найдем частную производную по
как величину постоянную, найдем частную производную по 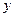 :
:
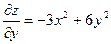 .
.
2) Имеем
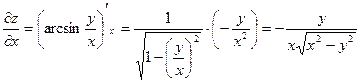 ;
;
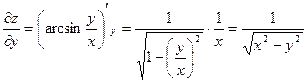 .
.
3) Здесь 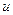 есть функция трех независимых переменных
есть функция трех независимых переменных 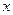 ,
, 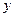 и
и 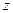 . При вычислении частной производной по каждой из этих переменных две другие следует считать постоянными величинами. Следовательно,
. При вычислении частной производной по каждой из этих переменных две другие следует считать постоянными величинами. Следовательно,
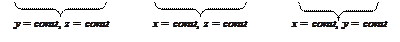
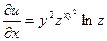 ;
; 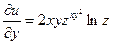 ;
; 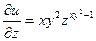
(так как при дифференцировании по 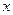 и по
и по 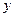 берется производная от показательной функции, а при дифференцировании по
берется производная от показательной функции, а при дифференцировании по 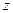 - от степенной функции).
- от степенной функции).
Задание 2: Вычислить полный дифференциал функции 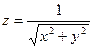 в точке
в точке 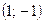 .
.
Решение: Находим частные производные:
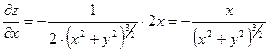 ;
;
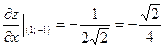 ;
;
 ;
;
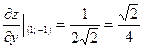 .
.
Таким образом, по формуле (1) получим 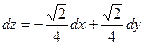 .
.
Задания для практической работы
1. Найдите частные производные следующих функций:
1) 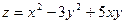 ; 3)
; 3) 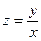 ; 4)
; 4) 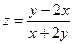 ;
;
5) 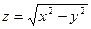 ; 6)
; 6) 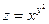 ; 7)
; 7) 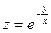 ;
;
8) 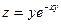 ; 9)
; 9) 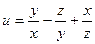 .
.
2. Найдите полные дифференциалы заданных функций:
1)  ; 2)
; 2) 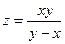 ; 3)
; 3) 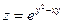 ;
;
4) 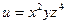 ; 5)
; 5) 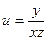 ; 6)
; 6) 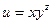 .
.
3. Вычислите значения полных дифференциалов функций:
1) 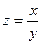 при
при 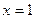 ,
, 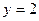 ,
, 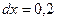 ,
, 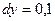 ;
;
3) 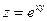 при
при 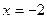 ,
, 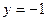 ,
, 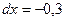 ,
, 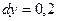 ;
;
4) 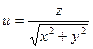 при
при 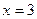 ,
, 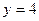 ,
, 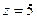 ,
, 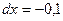 ,
, 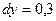 ,
, 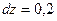 .
.
4. Проверьте, что функция 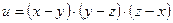 удовлетворяет уравнению
удовлетворяет уравнению 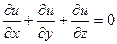 .
.
Вопросы для самоконтроля:
1. Что называется частной производной функции  по аргументу
по аргументу 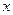 ?
?
2. Что называется частной производной функции  по аргументу
по аргументу 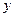 ?
?
3. Дайте определение полного дифференциала функции в некоторой точке.
4. В чем заключается свойство инвариантности полного дифференциала первого порядка?
Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.2, 2.3, 2.4, 2.5
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Богомолов Н.В. Практические занятия по математике: учеб. пособие для средних спец. учеб. заведений. – 6-е изд., стер. – М.: Высш. шк., 2003 – 495 с.
1.2 Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учеб. для студ. учреждений сред. проф. образования. – М.: Издательский центр «Академия», 2004. – 320 с.
1.3 Григорьев С.Г. Математика: учебник для студ. сред. проф. учреждений / под ред. В.А. Гусева. – 3-е изд., стер. – М.: Издательский центр «Академия», 2008. – 384 с.
1.4 Дадаян А.А. Сборник задач по математике: учеб. пособие. – М.: ФОРУМ: ИНФРА-М, 2008. – 352 с. – (Профессиональное образование).
1.5 Математика: учебник. – М.: ФОРУМ: ИНФРА-М, 2005. – 552 с. – (Серия «Профессиональное образование»)
2. Дополнительная:
1.1 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учеб. пособие для вузов. – 6-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2005. – 304 с.: ил.
1.2 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: учеб. пособие для вузов. – 6-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2005. – 416 с.: ил.
1.3 Малыхин В.И. Высшая математика: учеб. пособие. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2006. – 365 с. – (Высшее образование).
1.4 Шипачев В.С. Основы высшей математики: учеб. пособие для вузов / под ред. акад. А. Н. Тиханова. – 5-е изд., стер. – М.: Высш. шк., 2003. – 479 с.: ил.
1.5 Линьков В.М., Яремко Н.Н. Высшая математика в примерах и задачах. Компьютерный практикум: учеб. пособие / под ред. А.А. Емельянова. – М.: Финансы и статистика, 2006, - 320 с.: ил.
Информационные ресурсы:
| Сайты журналов | 1. Алгебра и анализ Режим доступа: http://www.mathnet.ru |
| Образовательные сайты | 1. Математика Режим доступа: http://energy.bmstu.ru/gormath/mathan2s/mainlist.htm 2. Учебник высшей математики Режим доступа: http://www.bez-dvoek.ru/matem/dif/index10.html 3. Математика Режим доступа: http://www.bymath.net/index.html 4. Лекции по высшей математике Режим доступа: http://www.mathelp.spb.ru/index1.htm 5. Математика Режим доступа: http://www.intuit.ru/courses.html |
| Порталы | 1. Информационно-коммуникационные технологии в образовании Режим доступа: http://www.ict.edu.ru |
Методические указания
по выполнению практических работ
для студентов специальностей
230115 Программирование в компьютерных системах
230401 Информационные системы (по отраслям)
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 566; Нарушение авторских прав?; Мы поможем в написании вашей работы!