ПРИМЕР 3. Корпорация использует график Гантта, представленный на рис

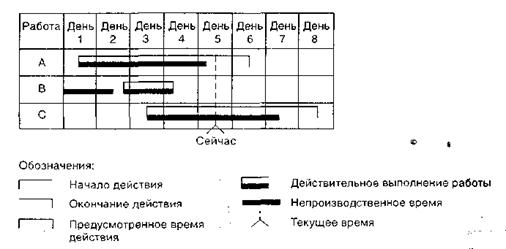
Корпорация использует график Гантта, представленный на рис. 11.3, чтобы проследить расписание выполнения трех заказанных работ: А. В и С. Каждая пара скобок на временной оси обозначает оценку начала и окончания работы, заклю­ченной внутри них. Сплошная полоса отражает действительное положение или прогресс в выполнении работы. Работа А, например, около половины дня отстает от расписания пятого дня выполнения работы. Работа В завершена после дневной профилактики, которая была произведена до начала работы. Работа С опережает расписание.

Рис. 11.3. Временной график Гантта для работ А, В и С

Метод назначений. Метод назначений представляет специаль­ный класс моделей линейного программирования, в которых рассматриваются задачи назначений и работ в зависимости от ресурсов. Примеры включают назначения работ по станкам, кон­трактов по строителям, людей по проектам и продавцов по территориям. Наиболее часто целью является достижение минимума суммарных денежных затрат или времени, необходимых для прак­тической реализации возникающих задач. Одной важной характе­ристикой проблем назначения является то, что назначению под­лежит только одна работа (или рабочий) на одну машину (или проект).

Каждая задача назначения может быть представлена таблицей. Числа в таблице будут денежными затратами или временными, ассоциирующимися с каждым конкретным назначением. Напри­мер, если в цехе имеются три свободных машины (А, В и С) и три новых работы, которые должны быть размещены, то ситуация может быть представлена таблицей.

Долларовые записи (занесения) представляют опенки фирмой затрат при назначении соответствующей работы на определенную машину.

Метод назначений – включает операции сложения и вычитания соответствующих чисел таблицы для того, чтобы найти самые низкие затраты, соответствующие условиям каждого отдельного назначения. Он включает следующие четыре шага.

1. Вычесть наименьшее число в каждой строке из каждого числа строки и затем вычесть наименьшее число в каждой колон­ке из всех чисел этой колонки.

Машина	Работа
А	В	С
R – 34	$11	$14	$6
S – 66	$8	$10	$11
Т – 50	$9	$12	$7

Этот шаг имеет своей целью понизить величины чисел в таблице до появления в ней серии нулей. Хотя числа и изменились в результате снижения их значений, в целом проблема остается эквивалентной исходной (первоначальной) и ее оптимальное ре­шение будет тем же, что и для исходной задачи.

2. Используя минимальное число вертикальных и горизон­тальных прямых линий, необходимо зачеркнуть все нули в табли­це. Если число линий равно либо числу строк, либо числу столб­цов в таблице, тогда мы можем сделать оптимальное назначение (смотри шаг 4). Если число линий меньше числа строк или; столбцов, мы переходим к шагу 3.

3. Вычтем минимальное неперечеркнутое число из всех других неперечеркнутых чисел. Добавим это же самое число ко всем числам, лежащим на пересечении любых двух линий. Вернемся к шагу 2 и продолжим процедуру до получения оптимального назначения.

4. Оптимальные назначения всегда будут находиться на местах размещения нулей в таблице. Направленный путь оценки назна­чений состоит в начальном отборе строки или колонки, которая содержит только один ноль. Мы можем сделать назначение в этот
квадрат и затем прочеркнуть линиями эту строку и столбец. Мы осуществим это назначение и продолжим вышеописанную проце­дуру, пока не назначим каждого человека или машину в соответствии с задачей.

Дата добавления: 2015-03-31