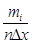Часть 3. Обработка многократных измерений

Задание

Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P=0.98.

44,22	44,33	43,89	44,15	44,35	43,96	44,06	44,99	44,30	44,26
44,17	44,30	44,12	44,20	44,69	44,15	44,13	44,04	44,03	44,19
44,10	44,19	44,10	44,19	44,26	44,37	44,26	44,08	44,25	44,38
44,02	44,40	44,28	44,41	44,17	44,38	44,07	44,32	44,20	44,24
44,11	44,09	44,30	44,41	44,05	44,10	43,94	44,21	44,29	44,21
44,24	44,11	44,11	44,19	44,41	44,06	44,11	44,20	44,37	44,19
44,37	44,36	44,40	44,50	44,26	44,28	44,04	44,23	44,29	44,05
44,20	44,04	44,18	44,22	44,33	44,16	44,01	44,28	44,18	44,22
44,36	44,17	44,11	44,30	44,17	44,25	44,16	44,35	44,32	44,15
44,15	44,24	44,22	44,40	44,30	44,15	44,30	44,05	44,13	44,02

1.Определяем среднее арифметическое и стандартное отклонение для данных таблицы:

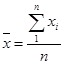
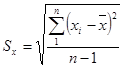
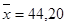
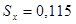
2.С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

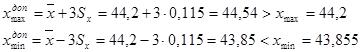
Таким образом, ни один из результатов не выходит за границы интервала [ 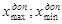], следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.

3.Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разобьем на k одинаковых интервалов .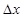

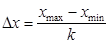
Принимая k=9, получим

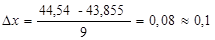
Т.к. в крайние интервалы попадает меньше 5 наблюдений, то объединим их с соседними.

m_i/n*∆x

Результаты производимых вычислений занесем в первую половину таблицы 1, и строим гистограмму.

43,84 44,08 44,16 44,24 44,32 44,40 45,56

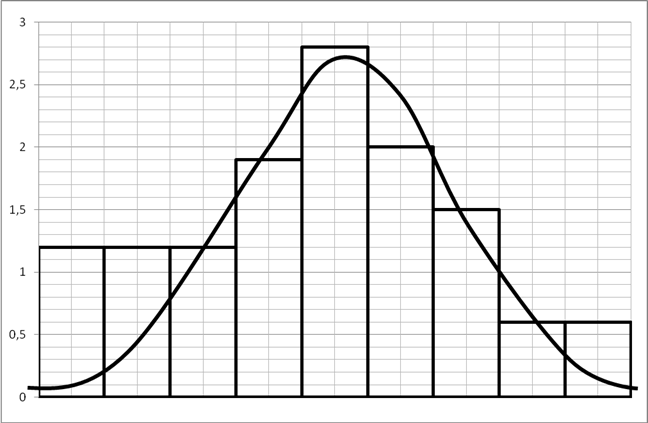
Из вида гистограммы можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

4.Проверка нормальности закона распределения по критерию Пирсона.

Т.к. в предыдущем пункте выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

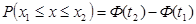
В данном случае значения x₁ и x₂ соответствуют началу и концу интервала. Для каждого из значений нужно рассчитать относительный доверительный интервал , а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t₁) Ф(t₂).

Найдя, таким образом, значения P_i для каждого интервала k_i, заполним соответствующие ячейки таблицы 1, а затем рассчитаем значение c² – критерия для каждого интервала.

Суммарное значение c²:

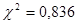
Определим табличное (критическое) значение c², задавшись доверительной вероятностью 0.94 и вычислив по формуле r=k-3 число степеней свободы:

r=6-3=3

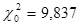
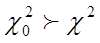
Таким образом, с вероятностью 0.98 гипотеза о нормальности распределения

вероятности результата измерения принимается.

Дата добавления: 2015-03-29