
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы представления выводов
|
|
|
|
Естественная форма представления выводов - их запись в виде последовательностей входящих в них слов. При этом для каждого слова последовательности указывается, из каких слов и с помощью какой продукции выводится такое слово.
Пример. Рассмотрим систему Поста, продукции которой содержат знания для вывода (построения) путей между вершинами графов.
Задание конкретного графа выполняется с помощью продукций-аксиом, задающих его ребра, и имеющих вид: (a, b), где a - начало ребра, а b - его конец.
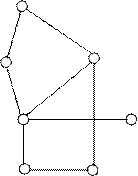
Например, рассмотрим граф G, приведенный на рис. 9.1:
 a 2
a 2
a 1 a 3
G
a 4 a 5
a 6 a 7
Рис. 9.1
Ребра приведенного графа задаются следующими продукциями:
p1 - p8:
(a 1, a 2), (a 2, a 3), (a 1, a 4), (a 3, a 4),
(a 4, a 5), (a 4, a 6), (a 3, a 7), (a 6, a 7).
Для того, чтобы указать, что ребра графа являются неориентированными, можно воспользоваться продукцией, указывающей на симметричность компонент пар, представляющих ребра:
p9: 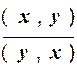 .
.
Наконец, правила определения пути, соединяющего произвольные две вершины графа, можно выполнять с помощью следующих двух продукций:
p10: 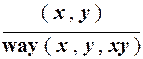 ;
;
p11:  .
.
Здесь слово way (x, y, z) означает, что z - это путь из x в y.
Продукция p10 представляет простейшее правило существования пути, записываемого как xy, между вершинами x и y, связанными между собой отдельными ребрами.
В продукции p11 представлено свойство транзитивности путей в графе, которое состоит в том, что если из вершины x в вершину y ведёт путь uy, а из вершины y в вершину z ведет путь yw, то x и z соединяет путь uw.
Данная система Поста состоит из:
1) основного алфавита A ={(,), “,”, way, a 1,..., a 7};
2) алфавита переменных V ={ x, y, z, u, w };
3) множества продукций P = {p1,..., p11}.
(Отметим, что символ запятой является элементом множества A.)
|
|
|
Рассмотрим вывод слова, содержащего путь между вершинами a 1 и a 7 в графе G.
1) (a 1, a 4) - применение аксиомы p3;
2) way (a 1, a 4, a 1 a 4) - получается применением продукции p10 к уже выведенному слову (a 1, a 4);
3) (a 3, a 4) - применение аксиомы p4;
4) (a 4, a 3) - получается применением продукции p9 к слову (a 3, a 4);
5) way (a 4, a 3, a 4 a 3) - применением продукции p10 к слову (a 4, a 3);
6) way (a 1, a 3, a 1 a 4 a 3) - получается с помощью p11, применённой к словам:
way (a 1, a 4, a 1 a 4) и way (a 4, a 3, a 4 a 3);
7) (a 3, a 7) - аксиома p7;
8) way (a 3, a 7, a 3 a 7) - выводится из слова (a 3, a 7) применением продукции p10;
9) way (a 1, a 7, a 1 a4a 3 a 7) - выводится с помощью продукции p11 из слов
way (a 1, a 3, a 1 a 4 a 3) и way (a 3, a 7, a 3 a 7).
Подобным образом можно обосновывать всякий вывод в этой и любой другой системе Поста.
При этом, если вывод в некоторой системе Поста является бесконечным, то для его представления могут потребоваться специальные соглашения, например при обосновании включения слов в вывод возможно появление последовательностей вида:
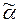 1,
1, 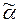 2,...,
2,..., 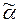 i,... " и так далее ".
i,... " и так далее ".
Возможно также использование записи вывода без объяснений, если в них нет необходимости.
При этом приведенный вывод перепишется как:
1) (a 1, a 4);
2) way (a 1, a 4, a 1 a 4);
3) (a 3, a 4);
4) (a 4, a 3);
5) way (a 4, a 3, a 4 a 3);
6) way (a 1, a 3, a 1 a 4 a 3);
7) (a 3, a 7);
8) way (a 3, a 7, a 3 a 7);
9) way (a 1, a 7, a 1 a 4 a 3 a 7).
Другим удобным и применяемым способом представления выводов в произвольных системах Поста являются деревья вывода.
Корню такого дерева приписывается последнее выводимое слово. Остальные вершины дерева помечены словами, входящими в вывод слова, приписанного корню, и продукциями, используемыми в этом выводе.
Всякая вершина дерева соединена с другими вершинами дерева с помощью ориентированных ребер по следующему правилу.
1. Если 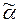 является применением некоторой аксиомы p, то дерево вывода этого слова имеет вид (рис. 9.2):
является применением некоторой аксиомы p, то дерево вывода этого слова имеет вид (рис. 9.2):
 p
p
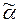
Рис. 9.2.
2. Если D 1,..., D k - это деревья вывода слов
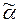 1,...,
1,..., 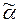 k и применение продукции p к этим словам позволяет вывести слово
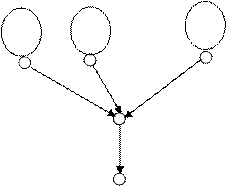
k и применение продукции p к этим словам позволяет вывести слово 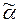 k+ 1, то дерево вывода такого слова имеет вид (рис. 9.3):
k+ 1, то дерево вывода такого слова имеет вид (рис. 9.3):
|
|
|
 |
D 1 D 2 D k
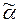 1
1 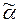 2...
2... 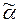 k
k
p
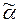 k+ 1
k+ 1
Рис. 9.3
Из определения дерева вывода следует, что если одно и то же слово применяется в выводе для получения нескольких разных слов, то дерево вывода содержит столько вершин, помеченных этим словом, сколько раз оно используется в выводе.
Кроме того, всякая вершина дерева, помеченная словом в основном алфавите, является корнем поддерева, являющегося деревом вывода этого слова.
Для приведенного выше примера вывода слова, представляющего путь из вершины a 1 в вершину a 7, соответствующее дерево вывода имеет вид, приведенный на рис. 9.4:
 p3p4
p3p4
(a 1, a 4) (a 3, a 4)
p10p9
way (a 1, a 4, a 1 a 4) (a 4, a 3)
p10
p11 way (a 4, a 3, a 4 a 3) p7
way (a 1, a 3, a 1 a 4 a 3) (a 3, a 7)
p10
p11 way (a 3, a 7, a 3 a 7)
way (a 1, a 7, a 1 a 4 a 3 a 7)
Рис. 9.4
Рассмотрим пример еще одной системы Поста, в которой выводятся все такие пары натуральных чисел в двоичной системе, из которых первое число больше второго.
Приводимые далее продукции реализуют определение отношения "больше" на множестве неотрицательных целых чисел.
1. Если длины записей сравниваемых чисел - разные, то запись большей длины представляет большее число.
2. Если длины записей сравниваемых чисел равны, то большим является такое число, в котором раньше встречается разряд, по значению больший соответствующего разряда другого слова при поразрядном сравнении слов слева-направо.
АКСИОМЫ: p1: 0 < 1, p2: 1 < 10, p3: 1 < 11.
Остальные продукции, разбитые на четыре группы:
1) p4: 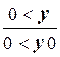 , p5:
, p5:  ,
,
2) p6: 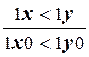 , p7:
, p7: 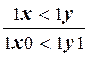 , p8:
, p8: 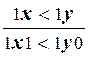 ,
,
p9: 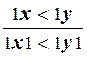 ,
,
3) p10:  , p11:
, p11: 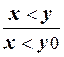 ,
,
4) p12: 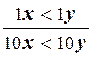 , p13:
, p13: 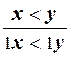 .
.
Приведенные продукции разбиты на группы. Такое разбиение основано на близости ролей продукций отдельных групп в выводах слов, представляющих любые верные неравенства между числами.
Покажем, что с помощью приведенных продукций выводится множество слов, представляющих в точности все правильные неравенства “меньше“ между целыми неотрицательными числами.
1. Непосредственно проверяется, что заключение всякой из продукций p1 - p13 представляет верное неравенство “меньше” для пары чисел, если посылка такой продукции представляет собой верное неравенство.
|
|
|
Следовательно, множество слов, выводимых в приведенной системе, представляет часть отношения “<“ между целыми неотрицательными числами.
2. Пусть s1... s m и d1... d n - двоичные записи натуральных чисел, между которыми выполнено отношение “<“.
2. 1. Если m < n, то вывод слова s1... s m < d 1... d n начинается либо со слова s1 < d1 d2, если s1 = 1, являющегося применением одной из продукций p 2, p3, либо со слова s1 < d1, если s1 = 0, являющегося применением продукции p1.
После этого с помощью продукций p4 - p9 можно достроить начальное слово до слова s1… s m < d1... d m+ 1.
Затем с помощью продукций p10 - p11 полученное слово можно достроить в слово s1 ... s m < d1... d n.
2. 2. Если m = n, то найдем такое наименьшее i, что
s i < d i.
Начнем вывод слова s1... s n < d1... d n со слова s i < d i, являющегося применением продукции p1.
Затем с помощью продукций p12 и p13 можно вывести слово s1... s i < d1... d i, для которого "j = 1,..., i -1(s j = d j). Процесс вывода этого слова начинается с применения продукции p13, которая добавляет первые слева от s i и d i единицы. Затем с помощью необходимого числа повторных применений продукции p12 можно разместить в обоих числах все нули между s i и d i и первыми единицами слева. Затем выполняется вставка в s1 ... s m и d1... d n следующих единиц левее s i и d i с последующим размещением нулей и т.д. пока не будут построено слово s1... s i < d1... d i
Из полученного слова с помощью продукций p6 - p9, позволяющих добавлять в них справа по одну символу можно вывести окончательное слово s1... s n < d1... d n.
Следовательно, множество слов, выводимых в приведенной системе продукций p1-p13, совпадает с множеством слов, которые представляют отношение“<“ между целыми неотрицательными числами.
Упражнение. 1. Добавить к продукциям p1 - p13 такие новые продукции, которые позволяют дополнительно выводить все слова вида x <> y, где x и y - неравные числа представленные в двоичной системе счисления. 2. Определить систему Поста, в которой выводятся слова вида x = y, где x и y записи неотрицательных целых чисел в двоичной системе.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 345; Нарушение авторских прав?; Мы поможем в написании вашей работы!